利用分形分析理論求解針刺非織造材料水平滲透系數

張一風 代婷婷 (中原工學院紡織學院，鄭州，450000)

利用分形分析理論求解針刺非織造材料水平滲透系數

張一風 代婷婷 (中原工學院紡織學院，鄭州，450000)

根據滌綸短纖針刺非織造材料的孔隙具有的分形特點，通過建立其縱向幾何結構模型，介紹了一種利用分形分析求解針刺非織造材料水平滲透率的方法，進而預測有關非織造材料的水平滲透系數。

非織造材料，分形分析，縱向幾何結構模型，水平滲透率

非織造土工材料因其獨特的三維纖維網結構，具有較高的水平滲透系數，廣泛地應用于需要排水功能的土木建筑工程中。目前，對于水平滲透性能的研究僅限于通過土工布水平滲透儀間接測得，且實驗過程繁瑣，耗時較長。隨著分形理論的發展，國內外的一些學者已經通過建立分形分析模型，求得了平紋織物的滲透率。本文主要利用分形理論，結合織物滲透率的分形分析模型，探討建立了針刺非織造材料的幾何結構模型，求其水平滲透系數。

1 分形分析與織物分形分析模型

1.1 分形分析

大自然中的很多物體，如海岸線、山川、河流、湖泊、島嶼等都是不規則的，用歐式幾何計算尺寸、面積、體積對它們都不適用。美籍數學家Mandelbort稱這些物體為分形，在此基礎上形成了研究分形性質及其應用的科學，稱為分形理論。具體表示如下:

分形物體的量度M(L)與測量的尺度L有關，即:

式中:Df——分維，是分形的基本參數;

M(L)——一個物體的長度、面積、體積或該

物體大部分的長度、面積、體積;

L——尺度。

同時，分形物體(如孔隙)的累積數N(如孔隙的數目)與孔隙的大小分布服從如下的標度關系:

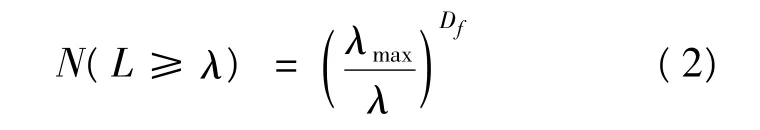
式中:λ，λmax——對于織物而言，分別為孔隙的尺

寸和最大尺寸。

1.2 織物分形分析模型

由式(2)可得織物中孔隙的總數Nn為:

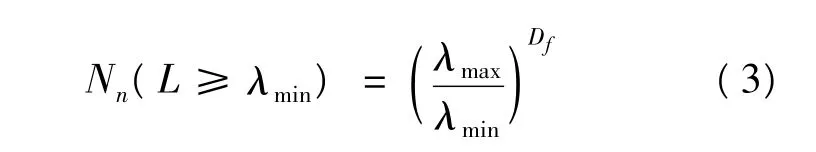
式中:λmin——孔隙最小尺寸。

假設流體流經織物的孔隙時，孔隙的直徑為λ，流經的通道長度為Ln(λ)，由于通道可能是彎曲的，所以可用分形形式表示為:

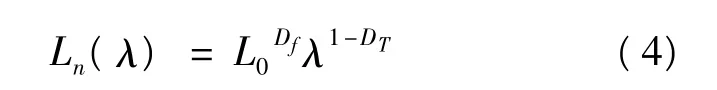
式中:DT——曲線(彎曲度)分形維數(DT=1表示該毛細管通道為直的，DT=2表示該毛細管通道的彎曲程度使其填滿整個平面);

L0——通道的代表性長度，因為DT的存在，Ln(λ)≥L0。

2 針刺非織造材料滲透率的分形分析模型

根據修正的Hagen-Poiseulle方程，流體流經針刺非織造材料某個通道的流量q(λ)為:

式中:μ——流體的黏性系數;

ΔP——壓力差。

結合式(3)，通過某個界面S的總流量Q可以通過對該界面內每個孔隙的流量q(λ)進行積分得到。在針刺非織造材料中，最小的孔隙可以看做趨近于0，所以:

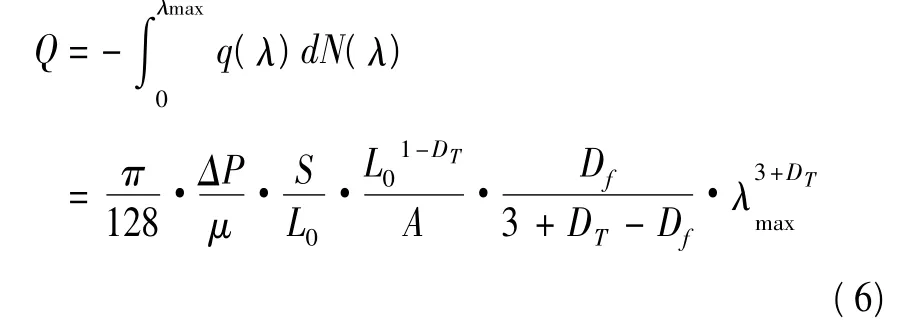
利用Darcy定理，可以得到針刺非織造材料的滲透率通用分形分析模型:

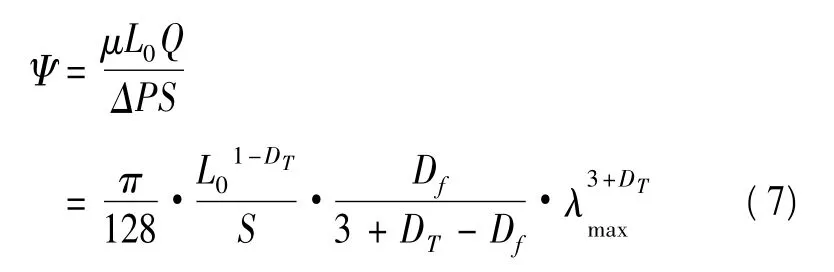
因為在液體流經針刺非織造材料時，流動通道可以看做是直的，即:DT=1，所以:

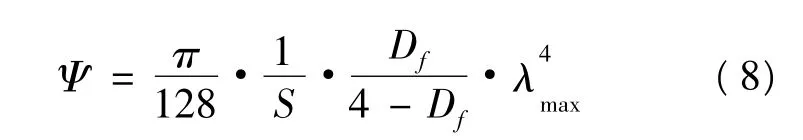
3 針刺非織造材料滲透率的求解

3.1 理論部分

針刺非織造材料內纖維分布錯綜復雜。為了便于量化材料內孔隙的尺寸，假設在垂直方向上纖維呈直線隨機平面交叉分布，孔隙的形狀近似為等邊三角形(見圖1陰影部分)，從而建立針刺非織造材料縱向的幾何結構模型。

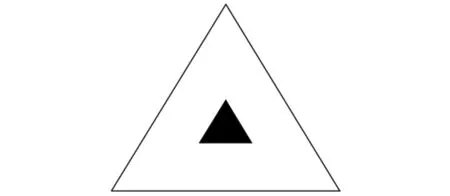
圖1 針刺非織造材料縱向的幾何結構模型

流體流經針刺非織造材料時，孔隙可假設為一組定向排列的毛細管，如圖2所示。

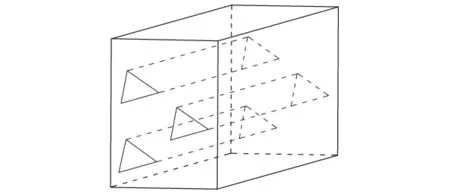
圖2 流體流經針刺非織造材料孔隙示意

3.2 實驗部分

試樣:面密度為650 g/m2的滌綸短纖針刺非織造材料。

實驗儀器:織物厚度儀、電子天平、數碼顯微鏡。

本實驗所用試樣采用HFT-Ⅱ型平面內水流量測試儀測得其水平滲透系數為0.32 cm/s。

采用織物厚度儀測得該試樣的厚度為4.35 mm，在800倍數碼顯微鏡下測得纖維的直徑為487.8 μm，等邊三角形孔隙的最大邊長為495.6 μm，如圖3 所示。

圖3 試樣的縱向幾何結構參數示意

3.3 計算部分

3.3.1 微單元面積S的求解

如圖3所示，纖維的直徑d為487.8 μm，則:

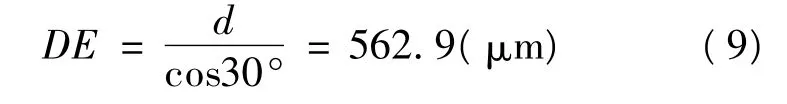
微單元的邊長:

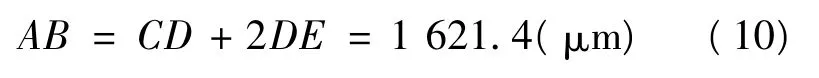
由此可得為單元的面積:

3.3.2 最大孔隙直徑 λmax的求解

由于Darcy定理只對圓形的孔隙有效，而模型中的孔隙為三角形，所以λmax可以近似為:

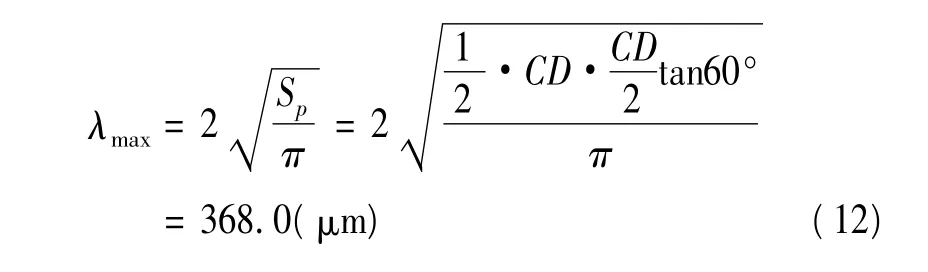
式中:Sp——孔隙的面積。

3.3.3 分維 Df的求解

根據式(1)，孔隙的面積Sp可以表示為:

用面積相等的邊長為L的正方形代替微單元的面積，則有:

根據孔隙率的定義，孔隙率φ:

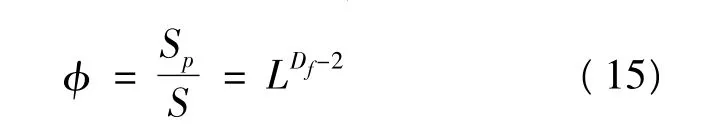
對于織物，其孔隙率可以表示為:

式中:ρn——滌綸短纖針刺非織造材料的面密度;

ρ——滌綸的密度(1.38 g/cm3);

δ——材料的厚度。

結合式(15)和(16)，得:

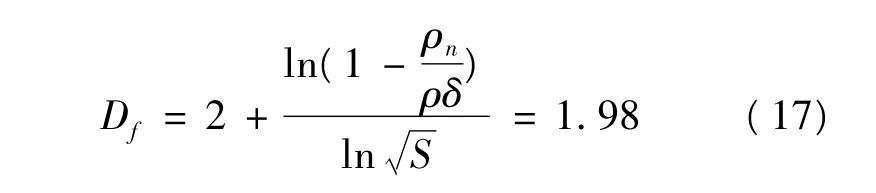
3.3.4 針刺非織造材料水平滲透系數的求解

將求得的參數S、λmax以及Df代入式(8)，可得滌綸短纖針刺非織造材料的水平滲透率Ψ:

根據滲透率與滲透系數的換算公式，得滲透系數K:

式中:ρ0——水的密度(998.2 kg/m3);

g——重力加速度(9.8 m/s2);

μ——水的黏度系數(1.005 ×10－3m/s2)。

4 結論

利用分形理論結合織物滲透率的分形分析模型，探討建立針刺非織造材料的幾何結構模型，求解其水平滲透率，進而預測有關非織造材料的水平滲透系數的方法是一項有意義的研究。

(1)試樣水平滲透系數的實驗值(預測值)與采用HFT-Ⅱ型平面內水流量測試儀測得的實測值的比較結果是:實測值0.32 cm/s＜實驗值0.38 cm/s。

(2)針刺非織造材料的實際水平滲透系數近似于預測值，說明利用分形分析模型求解非織造材料的水平滲透系數是可行的，但本課題只對一種規格的非織造材料進行了實驗，具體可行性還有待進一步分析。

(3)相對于針刺非織造材料錯綜復雜的縱向形態，實驗中建立的幾何結構模型比較簡單，估計實驗值比實測值略大的原因正在于此。

［1]YU Boming，LEE L J，CAO Hanqiang.A fractal inplane premeability model for fabrics［J].Polymer Composites，2002，23(2):201-221.

［2]陸振乾，錢坤.利用分形理論求解織物滲透率［J].紡織學報，2006，27(2):17-24.

［3]劉麗芳，王衛章，儲才元，等.非織造土工布孔徑分布與滲透性能關系的研究［J].產業用紡織品，2003，21(3):17-20.

Calculate the horizontal permeability factor of nonwovens by the fractal theory

Zhang Yifeng，Dai Tingting (School of Textile，Zhongyuan University of Technology)

Base on fraction property of pore in polyester fiber needle-punched nonwovens，the horizontal permeability ratio of needle-punched nonwovens was calculated by fraction method through establishment of vertical structure model.The horizontal permeability factor of the nonwovens was forecasted.

nonwovens，fractal analysis，vertical structure model，horizontal permeability

TS171;TS176.3

A

1004－7093(2010)11－0031－03

2010－08－17

張一風，男，1958年生，教授級高工。主要從事紡織產品及工藝的研發和教學工作。