基于DEA模型的資源型城市經濟發展效率實證研究

□傅利平 王中亞 [天津大學 天津 300072]

基于DEA模型的資源型城市經濟發展效率實證研究

□傅利平 王中亞 [天津大學 天津 300072]

本文基于DEA方法中的C2R模型對我國34個典型資源型城市經濟發展效率進行實證研究。結果表明，石油和冶金城市經濟發展效率較高，而煤炭和森工城市經濟發展效率較低。我國很多資源型城市規模較小，沒有能夠真正發揮出區域經濟發展增長極作用。資源型城市要提高經濟發展效率，實現可持續發展，必須在實施產業轉型的過程中不斷加大基礎設施投資力度，適度擴大城市規模。

資源型城市；經濟發展效率；DEA；聚類分析

引言

資源型城市是因自然資源的開采而興起或發展壯大，資源型城市的興起和發展不僅加快了我國的城市化進程，而且為國家經濟建設做出了突出貢獻。近年來，面對科技革命帶來的新能源、新材料的強勁沖擊，長期以來堅持“資源立市”傳統模式的資源型城市的經濟發展水平每況愈下，很多新矛盾和新問題不斷出現，如資源枯竭、成本激增、效益滑坡、冗員增多等[1]。由于資源型城市依托的自然資源、地理區位、城市規模不同，這些城市的發展差別很大，分析不同資源型城市經濟發展的規律性，進而揭示制約發展的因素，對資源型城市的經濟發展具有重要指導意義。如何評價資源型城市的經濟發展效率，如何制定相關政策，使眾多資源型城市在區域經濟發展過程中發揮“增長極”作用，是資源型城市經濟發展研究中的重點和難點[2]。

本文在簡要介紹DEA方法及模型、聚類分析方法的基礎上，選取若干投入和產出指標，利用《中國城市統計年鑒》數據，對我國34個典型的地市級資源型城市的經濟發展效率進行實證研究和聚類分析，進而探討模型計算結果對資源型城市制定經濟發展政策的啟示。

一、方法和模型簡介

（一）DEA方法和模型

數據包絡分析（Data Envelopment Analysis）簡稱DEA，是運籌學、管理科學和數理經濟學交叉研究的一個新的領域，它是由著名的運籌學家Charnes、Cooper和Rhodes等人于1978年在“相對效率評價”概念的基礎上發展起來的，是評價同類型決策單元相對有效性的一種系統分析方法[3]。

DEA方法的基本思想是建立一個線性規劃模型，對各個決策單元（Decision Making Unit，簡記為DMU）做出相應的評價。作為一種效率評價方法，DEA方法能夠對同一系統內的各個決策單元的有效性進行評價，它主要是根據系統的輸入和輸出指標，建立相應的評價模型，從而得到每個評價單元的效率評價值。DEA方法具有以下優點：相對的客觀性；不需要考慮量綱，進而不需要進行歸一化處理，簡化了評價工作的流程；全面評估DMU的生產狀況；為主管部門提供許多管理信息[4]。

實際上，DEA方法并非完美無缺，它也存在著一些局限性和問題：測量誤差和其他噪聲將會影響前沿的形狀及位置；異常值可能影響到結果；排除掉一個重要的投入或產出要素將會導致有偏結果；所獲得的效率值僅是對于樣本中的最佳廠商而言，增加其他廠商于樣本中將減少效率值等[5]。這提醒研究者在運用這一模型評價決策單元效率時，必須十分謹慎，最好能把DEA評價和通常的相對指標評價結合起來。

DEA方法包括很多模型，諸如C2R模型、C2GS2模型、C2W模型、C2WH模型、C2WY模型和逆DEA模型等[6]。

本文用來評價各個資源型城市經濟發展效率的模型是DEA方法中的基于投入的具有非阿基米德無窮小 的C2R模型，它是原理比較簡單但運用較為廣泛的一個模型。模型的表達式如下：

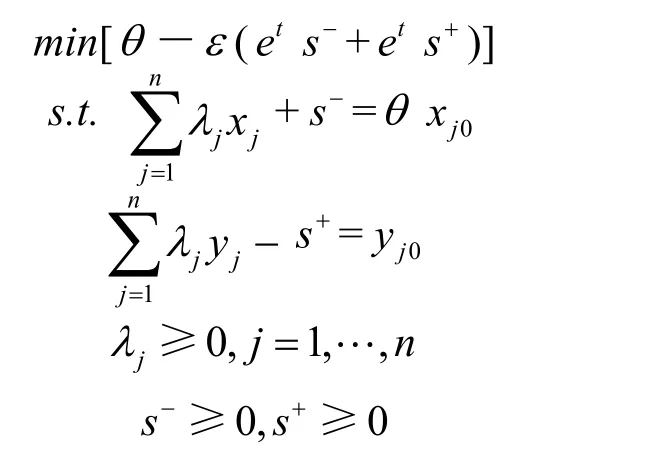
（二）聚類分析法

聚類分析是統計學中研究“物以類聚”問題的多元統計分析方法。聚類分析中，個體間的“親疏程度”是極為重要的，它將直接影響最終的聚類結果。對“親疏程度”的測度有兩個角度：一是個體間的相似程度，二是個體間的差異程度。個體間的相似程度通常可采用簡單相關系數或等級相關系數來衡量。個體間差異程度通常通過某種距離來測度。如果所涉及的變量全部為定距型變量，那么個體間距離的定義通常有以下幾種方式：歐氏距離、平方歐氏距離、切比雪夫距離、Block距離、明考斯基距離、夾角余弦距離等。

常見的聚類分析方法有層次聚類和K-Means聚類。層次聚類的聚類方式又分為兩種：凝聚方式聚類和分解方式聚類。而統計分析軟件SPSS16.0中的層次聚類采用的是凝聚方式[7]。本文中采用的是層次聚類法，進行聚類分析的變量為依據DEA模型計算的資源型城市經濟發展效率值θ和市轄區人均地區生產總值兩個指標。

二、研究對象、指標選取與模型計算結果

（一）研究對象

關于我國資源型城市的界定標準和數量問題，學術界存在著一定的分歧，其中，張以誠、周海林、周德群、王青云等專家和學者的觀點具有代表性。據國家計委宏觀經濟研究院課題組的研究成果（王青云執筆），我國現有資源型城市118個[8,9]。本文選取其中34個典型的地市級資源型城市作為研究對象，其具體名稱和分布見表1所示。

（二）指標選取及說明

為了統一口徑，同時也為了使數據具有可比性，借鑒參考文獻[2]的做法，本文重新篩選了資源型城市經濟系統的投入和產出指標。由于工業總產值是地區生產總值的一部分，所以工業總產值不宜與地區生產總值同時進入DEA模型中的產出指標體系。最終，本文選取市轄區勞動力就業人口數（x1）、建成區面積（x2）、市轄區全社會固定資產投資總額（x3）、市轄區科學教育支出（x4）作為資源型城市經濟系統的投入指標，它們代表了城市經濟系統的各種要素投入。其中，建成區面積是指城市行政區內實際已成片開發建設、市政公用設施和公共設施基本具備的區域。對于核心城市而言，它包括集中連片的部分以及分散的若干個已經成片建設起來，市政公用設施和公共設施基本具備的地區。對于一城多鎮城市而言，它包括由幾個連片開發建設起來的，市政公用設施和公共設施基本具備的地區組成。建成區范圍，一般是指建成區外輪廓線所能包括的地區，也就是這個城市實際建設用地所達到的范圍。建成區面積反映一個城市經濟發展的土地要素投入和城市規模大小。選取市轄區地區生產總值（y1）、市轄區社會消費品零售總額（y2）、市轄區地方財政一般預算內收入（y3）作為資源型城市經濟系統的產出指標，它們從不同角度描述了城市發展的成果。

市轄區勞動力就業人口數由市轄區年末單位從業人員數和城鎮私營個體從業人員數兩項指標數值加總得到，它體現了資源型城市人力資源投入的數量。市轄區科學教育支出由市轄區科學支出和教育支出加總得到。選擇科學教育支出作為投入指標的理由在于，知識經濟時代，勞動力的投入不僅要關注量，更要關注質，科學教育投入是人力資本投資的主要途徑之一[10]。在我國絕大多數資源型城市中，人力資源普遍存在著數量充裕與質量較低的矛盾，所以必須加大對人力資本的投資力度[11]。

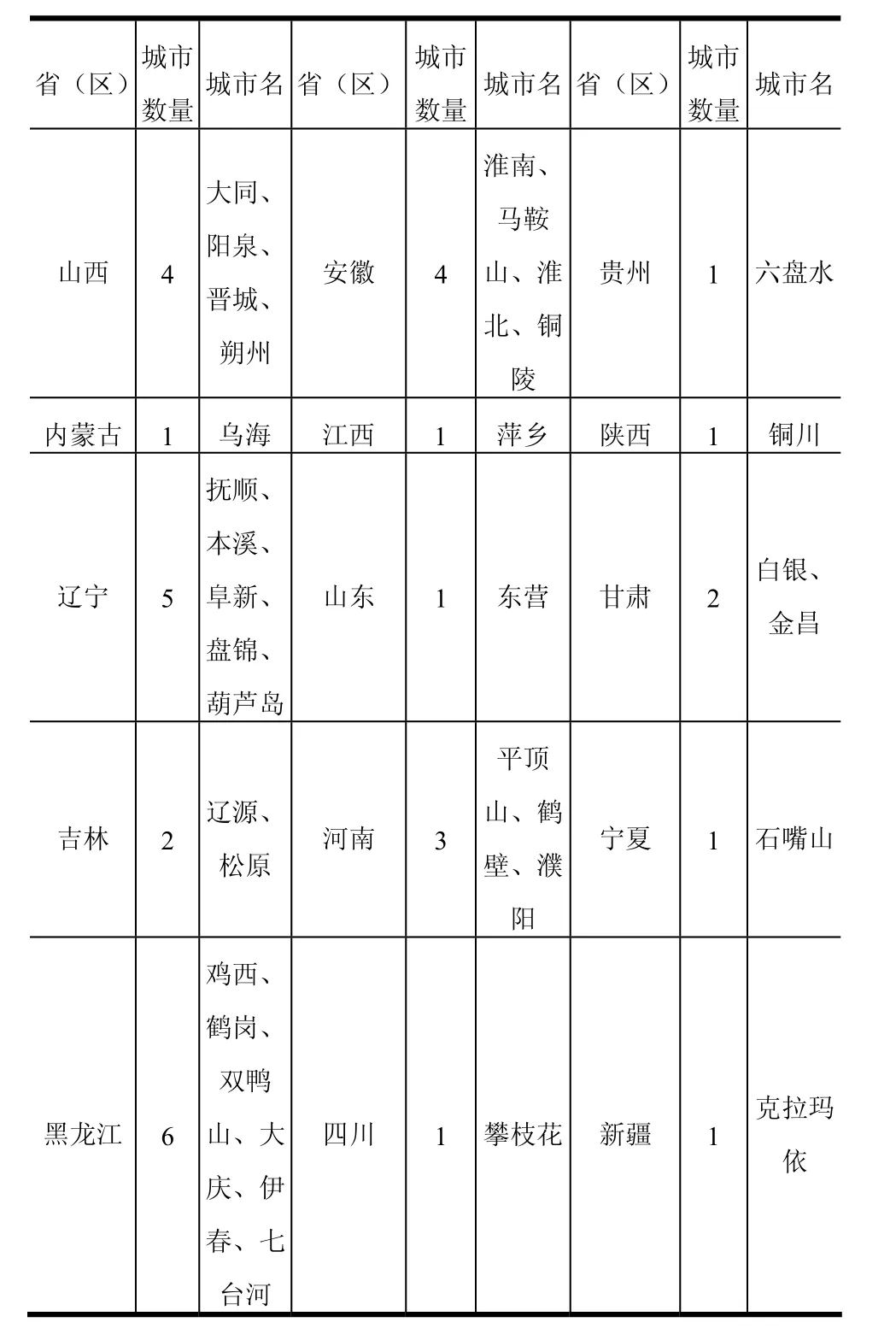
表1 典型地市級資源型城市及其分布

所有指標原始數據均來源于《中國城市統計年鑒2008》。

（三）模型計算結果

利用DEAP軟件求得不同資源型城市經濟發展的總體效率[12]，經過整理的輸出結果，見表2所示，其中，為城市發展的效率；規模報酬分為規模報酬不變（CRS）、規模報酬遞增（IRS）和規模報酬遞減（DRS）三種情況。

以表2中的資源型城市經濟發展相對效率值和《中國城市統計年鑒2008》中的各市市轄區人均地區生產總值為變量，利用SPSS16.0統計分析軟件中的聚類分析模塊，可以得到經濟發展效率從高到低的四個聚類：聚類I包括大慶和東營，聚類II包括盤錦、克拉瑪依、馬鞍山、銅陵和金昌，聚類IV包括雙鴨山、七臺河、淮南、淮北和鶴壁，其余城市屬于聚類III。借鑒參考文獻[8]的做法，本文把資源型城市分為四類，即石油城市、冶金城市（有色冶金城市和黑色冶金城市）、煤炭城市和森工城市。我國34個典型地市級資源型城市的發展效率聚類與城市類型的關系，如表3所示。

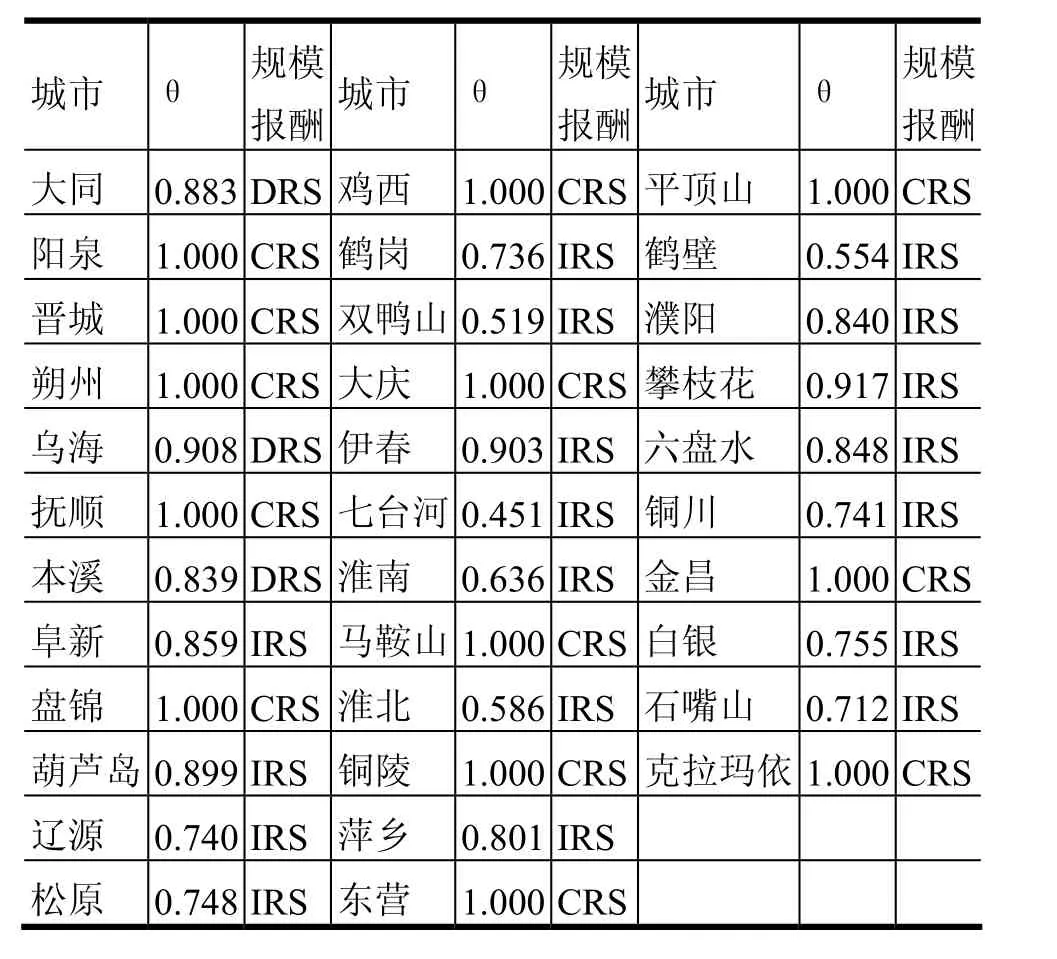
表2 典型資源型城市DEA模型計算結果

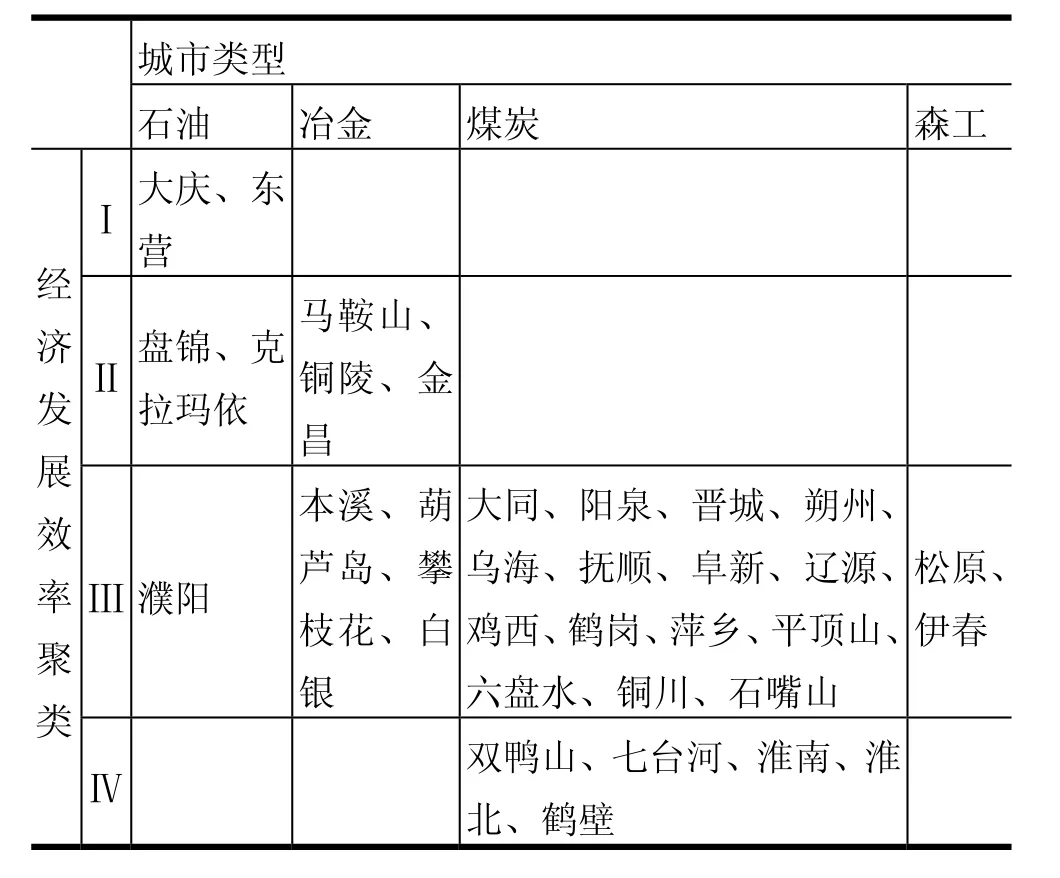
表3 典型資源型城市經濟發展效率聚類與城市類型矩陣

三、結果分析

（一）效率分析

由表2的計算結果可知，2007年我國34個典型資源型城市中有13個處于總體效率的前沿面，它們是陽泉、晉城、朔州、撫順、盤錦、雞西、大慶、馬鞍山、銅陵、東營、平頂山、金昌和克拉瑪依。而雙鴨山、七臺河、淮北和鶴壁的經濟發展效率很低，其經濟效率值 均低于0.6，并且這4個城市均為煤炭資源型城市。雖然在34個資源型城市中，有13個經濟發展效率值為1，但這只是資源型城市內部之間的比較，實際上，資源型城市與非資源型城市相比，資源枯竭城市與資源未枯竭城市相比，在經濟發展效率上差距依然很大。

（二）經濟發展效率聚類分析

由表3的聚類分析結果可知，在所有的資源型城市，石油和冶金城市總體效率較高，而煤炭和森工城市總體效率較低。大慶市和東營市的經濟發展效率最高，二者均為石油城市；雙鴨山、七臺河、淮南、淮北和鶴壁的經濟發展效率最低，它們皆為煤炭城市。這說明，資源型城市經濟發展效率與其所依托的資源種類有密切關系，資源型城市發展必然受到資源儲量、國際能源結構甚至居民消費結構的影響。根據資源型產業的生命周期理論，資源型城市必須未雨綢繆，適時進行產業轉型，產業轉型是資源型城市可持續發展的客觀要求[13]。無論是對于經濟發展效率較低的煤炭城市，還是對于經濟發展效率較高的石油城市，必須通過發展接續產業或者發展替代產業實現所謂的“小轉型”或“大轉型”[14]。

（三）規模報酬分析

由表2可知，18個資源型城市處于規模報酬遞增階段，13個資源型城市處于規模報酬不變階段，3個城市處于規模報酬遞減階段，分別占被研究對象的52.94%、38.24%和8.82%。這說明我國很多資源型城市還沒有達到經濟學上所講的“經濟規模”。加大固定資產投資強度對于資源型城市提高經濟發展效率，進而擺脫“資源詛咒”現象具有重要作用[15]。因此，對于大部分資源型城市而言，要真正發揮其在區域經濟發展中的“增長極”作用，獲得規模經濟，必須進一步加快城市化進程，以城市化促進經濟發展，加強城市基礎設施建設，合理規劃，拉大城市框架，提升城市規模。

四、結束語

本文利用DEA方法中的C2R模型和多元統計分析中的聚類分析法，對我國34個典型資源型城市經濟發展效率進行了實證研究，并對計算結果進行了初步分析。實踐證明，DEA方法在評價資源型城市經濟發展效率方面是相當有效的。若利用該方法和多年份統計數據，對資源型城市經濟發展效率進行動態研究，必將對揭示資源型城市發展規律大有裨益。此外，還可以通過計算各投入要素的影子價格來分析各種要素投入量是否充足。這為筆者下一步研究指明了方向。

由于每個城市在地理區位、資源稟賦和歷史基礎等方面不盡相同，導致目前我國資源型城市的經濟發展效率存在明顯差異。這就要求資源型城市理性地看待發展過程中出現的各種困難和挑戰，不斷調整自己的發展戰略，提高城市經濟發展效率，盡量縮小與非資源型城市經濟發展的差距，從而最終實現全面、協調和可持續的發展。

[1] 武春友, 葉瑛. 資源型城市產業轉型問題初探[J].大連理工大學學報(社會科學版), 2000, (3): 6-9.

[2] 湯建影, 周德群. 基于DEA模型的礦業城市經濟發展效率評價[J]. 煤炭學報, 2003, (4): 342-347.

[3] 盛昭瀚, 朱喬, 吳廣謀. DEA理論、方法與運用[M].北京: 科學出版社, 1996.

[4] 吳育華, 劉喜華, 郭均鵬. 經濟管理中的數量方法[M]. 北京: 經濟科學出版社, 2008.

[5] 蒂莫西.J.科埃利, 等. 效率與生產率分析引論[M].北京: 中國人民大學出版社, 2008.

[6] 魏權齡. 數據包絡分析(DEA)[J]. 科學通報, 2000,(17): 1793-1806.

[7] 薛薇. SPSS統計分析方法及應用[M]. 北京: 電子工業出版社, 2009.

[8] 國家計委宏觀經濟研究院課題組. 我國資源型城市的界定與分類[J]. 宏觀經濟研究, 2002, (11): 37-39.

[9] 王青云. 資源型城市經濟轉型研究[M]. 北京: 中國經濟出版社, 2003.

[10] 西奧多·舒爾茨. 對人進行投資: 人口質量經濟學[M]. 北京: 首都經濟貿易大學出版社, 2002.

[11] 黃溶冰, 王麗艷. 資源型城市轉型中的人力資本投資與分享[J]. 科學·經濟·社會, 2008, (111): 41-44.

[12] COELLI T. A Guide to DEAP Version 2.1: A Data Envelopment Analysis (computer) Program[R]. Armidale,Australia: University of New England, 1996.

[13] 張米爾, 武春友. 資源型城市產業轉型障礙與對策研究[J]. 經濟理論與經濟管理, 2001, (2): 35-38.

[14] 姜春海, 于立.資源枯竭型城市產業轉型研究[J].南大商學評論, 2007, (1): 65-82.

[15] 黃溶冰, 王躍堂. 資源型經濟如何擺脫“資源詛咒”——基于中國的經驗證據[J]. 江海學刊, 2009, (2): 81-87.

編輯 何 婧

Empirical Study on Economic Development Efficiency of RBC Based on DEA Model

FU Li-ping WANG Zhong-ya
(Tianjin University Tianjin 300072 China)

This paper makes demonstration analysis about economic development efficiency of 34 classical resource-based cities in China. The DEA model and cluster analysis are applied during the research. As a conclusion, it finds that the 34 RBC vary considerably in economic development efficiency. Generally speaking,the better petroleum cities and metal cities are, the worse coal cities and forest cities are. It is necessary for RBC to enlarge their economic scales. In the meantime, industrial conversion is of great importance for the Chinese RBC’s sustainable development in the future.

resource-based cities; economic development efficiency; DEA; cluster analysis

F290

A

1008-8105(2010)06-0020-04

2010 - 06 - 29

傅利平（1963 -）女，天津大學管理學院教授，博士生導師；王中亞（1978 -）男，天津大學管理學院技術經濟及管理專業博士研究生.