兩四能級型原子系統相位噪聲的BangBang控制

王艷輝賈春霞姜春蕾

（湖南科技大學 物理學院, 湘潭 411201）

0 引 言

糾纏是量子系統得以進行量子計算與量子通訊等必不可少的資源。環境和系統的相互作用使量子系統的糾纏退化甚至消失。因而消相干的抑制和糾纏的保持是量子通訊和量子計算等領域亟待解決的問題[1]，也是當前研究的熱點之一[2~5]。在所有的噪聲抑制方案中，BangBang（BB）控制被認為是一個有效的方案。BangBang控制，也稱動力學解耦的方法，它起源于1968年Haeberlen和Waugh運用量子平均場效應思想設計脈沖序列控制系統的有效哈密頓量[6]。隨后它被發展成核磁共振技術中的解耦和重聚焦技術[6,7]。Viola和Lloyd在此基礎上引入了動力學解耦方案，用動力學的方法壓制單量子比特的消相干，從而保持量子系統態的相干性[8,9]。課題組前期的工作已經研究了單個多能級原子在噪聲作用下的BB解耦問題[10~17]。量子通訊和量子信息都涉及多粒子系統，而兩粒子系統是一個最基本的多粒子系統，因而，當前研究內容為兩個四能級Ξ型原子組成的系統處于相位噪聲環境下的BB解耦方案。

1.子系統和環境相互作用的哈密頓量

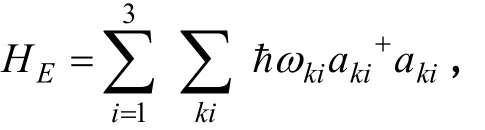
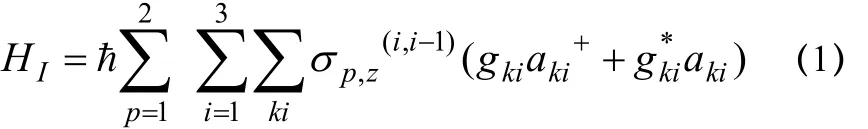
這里 gki(i=1,2,3)是原子躍遷與熱庫交換激發的耦合常數，其中包含了不同相位消相干的相對幾率幅的系數。

2.力學解耦機制[16]

動力學解耦方法使用共軛 BB脈沖來過濾系統和環境整個哈密頓量中不希望的相互作用部分，從而實現對量子系統的動力學行為進行控制，對系統量子噪聲進行消相干抑制。BB脈沖是受控的幺正脈沖，相當于具有任意大的強度的脈沖操作，可以在忽略的時間t內開啟或關閉它。

由于受環境的相互作用，原子系統在噪聲作用下的自由演化哈密頓量為H′=H+HI。在整個系統Sab上重復地循環地進行一系列BB控制操作V={νk} ,(k =0,?1)，操作間都間以系統的自由演化。通過恰當的選擇操作集 V ={νk}，可以達到消除系統的自由演化哈密頓量H′中不希望的部分 HI，即實現了使系統和環境解耦的目的，成功地抑制了系統噪聲。

考慮一個完整的循環。令 U (Δt )=exp(?iΔtH′)為在循環中系統的自由演化，持續時間為Δ t= t(。恰當選擇解耦操作 V ={νk}，使得它滿足解耦條件

在解耦脈沖序列的作用下，單個循環時間cT中復合系統abS的演化可以由算符

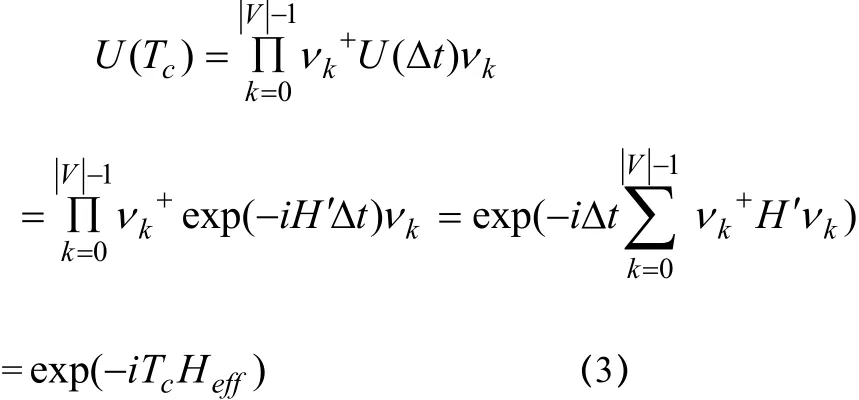
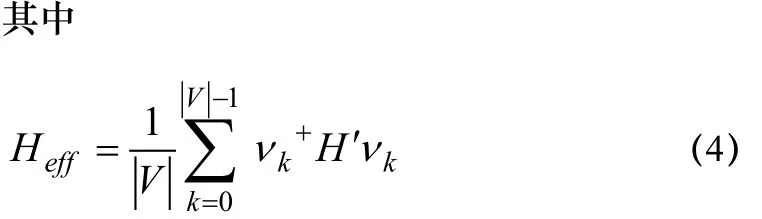
3.個四能級Ξ型原子組成的系統相位消相干的BB 解耦方案

從上節分析可知，要給出解耦方案，最主要的是要找出解耦操作集合。對于處于相位噪聲環境的兩個四能級Ξ 型原子組成的系統，令

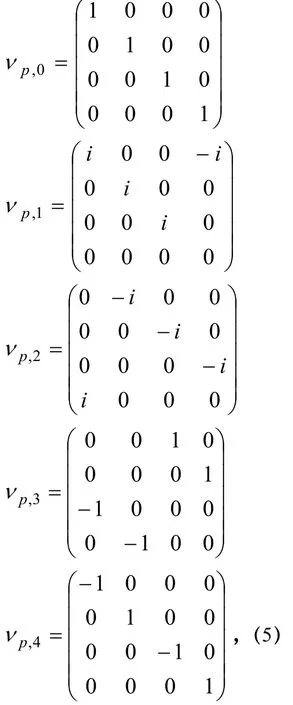
其中 p={1,2}表示操作作用于第一個粒子或第二個粒子上，發現解耦操作集為V==1,j,i,j =0,1,2,3,4}，由十六個解耦操作組成。

把解耦操作集V={νk}代入解耦條件，得

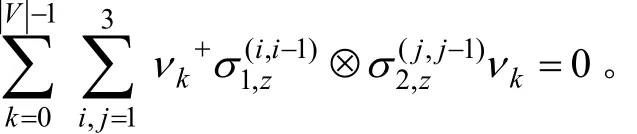
4.結

兩個四能級Ξ型原子系統在相位消相干環境下BangBang 解耦方案的解耦操作集合。分析表明，在理想的情況下，所給的解耦操作集合能很好的壓制兩個四能級Ξ型原子所組成的系統的相位噪聲。

[1]Long G L, Li Y S, Zhang W L and Tu C C, Dominant gate imperfection in Grover’s quantum search algorithm[J]. Phys.Rev. A , 2000, 61 042305

[2]Uhrig G S, Keeping a quantum bit alive by optimized π-pulse sequences[J]. Phys. Lett., 2007, 98, 100504

[3]Lee B, Witzel W M＆Das Sarma S, Universal pulse sequence to minimize spin dephasing in the central spin decoherence problem[J]. Phys. Rev. Lett., 2008, 100,160505

[4]Biercuk M J, et al. Optimized dynamiccal decoupling in a

model quantum memory[J], Nature, 2009, 458, 996-1000[5]Du J F, Rong X, Zhao N, Wang Y, et al., Preserving electron spin coherence in solids by optimal dynamical decoupling[J],Nature, 2009, 461, 08470

[6]Haeberlen U, Waugh J S. Coherent Averaging Effects in Magnetic Resonance[J]. Phys. Rev., 1968, 175:453–467.

[7]Zanardi P,Symmetrizing evolutions[J]. Phy. Lett. A, 1999,258 (1): 77–82.

[8]Viola L, Lloyd S, Knill E. Universal Control of Decoupled

Quantum Systems[J]. Phy. Rev. Lett., 1999, 83: 4888.

[9]Viola L, Lloyd S, Knill E., Dynamical suppression of decoherence in two-state quantum systems[J]. Phy. Rev. A,1998,58:2733

[10]Liu X S et al., Dynamical control of adiabatic decoherence in the single three-level atom[J],J. Opt. B: Quantum and Semiclassical Optics, 2009, 7(9), 268-263

[11]Liu X S, Wu R B, Liu Y, Liu W Z and Long G L,Decoupling Bang-Bang Group for Adiabatic Decoherence Control in a Three-Level Atom[J],Commun. Theor. Phys,2005, 44 (5):810-814

[12]Liu X S, Liu W Z, Wu R B, and Long G L, Control of State Localization in a two-level quantum system[J], J. Opt. B:Quantum. Semiclass.Opt., 2005, 7, 66

[13]Liu X S and Liu Y, Dynamical Suppression of Decoherence in Two-Qubit quantum Memory[J], Commun.Theor. Phys. 44(3): 459-462 Sep. (2005)

[14]Wang Y H and Liu X S and Long G L, General Dcoherence Suppression in Three-LevelAtom in V- and Ξ-Configurations[J], Commun. Theor. Phys., 2008,49(4):881-886 Apr. (2008)

[15]Wang Y H and Liu X S and Long G L, Suppression of Phase and amplitude Damping in a Three-Level Atom in λ-Configuration Using Bang-Bang Controls[J], Commun.Theor. Phys., 2008, 48(1):71-74

[16]Wang Y H and Liu X S and Long G L,Supression of Amplitude Decoherence in Arbitrary n-Level Atom in Ξ-Configuration with BangBang Controls[J], Commun.Theor. Phys., 2008, 49(6):1432-1434

[17]Wang Y H, Hao L, Zhou X and Long G L, Behavior of quantum coherence of Ξ-type four level atom under bang-bang control[J]. Opt. Commun.,2008, 281: 4793-4799.