基于時(shí)間序列模型的可轉(zhuǎn)換債券收益率的實(shí)證研究

曾立波黃麗芳

(湖南科技學(xué)院 數(shù)學(xué)與計(jì)算科學(xué)系，湖南 永州 425100)

1.引言

近年來(lái),我國(guó)證券市場(chǎng)取得了突飛猛進(jìn)的發(fā)展。隨著證券市場(chǎng)的規(guī)模不斷擴(kuò)展,證券是市場(chǎng)內(nèi)容不斷加深,引入新的金融品種,完善市場(chǎng)結(jié)構(gòu)已成為一種必然的趨勢(shì)，上市公司和國(guó)有重點(diǎn)企業(yè)發(fā)行可轉(zhuǎn)換債券就是一種新的嘗試。可轉(zhuǎn)換公司債券，是一種公司債券，它賦予持有人在發(fā)債后一定時(shí)間內(nèi)，可依據(jù)本身的自由意志，選擇是否依約定的條件將持有的債券轉(zhuǎn)換為發(fā)行公司的股票或者另外一家公司股票的權(quán)利。對(duì)于投資者來(lái)說(shuō), 其吸引力主要在于相對(duì)安全的債務(wù)所帶來(lái)的直接安全性,以及如果公司股票價(jià)格上漲債券可以轉(zhuǎn)換成股權(quán)的可能性[1]。

由于可轉(zhuǎn)換債券的價(jià)格與其收益率密切相關(guān)，因此對(duì)可轉(zhuǎn)換債券收益率研究對(duì)其價(jià)格預(yù)測(cè)有極其重要的作用[2,3]。而時(shí)間序列模型在金融資產(chǎn)收益率研究方面應(yīng)用相當(dāng)廣泛，因此本文利用時(shí)間序列模型和到2009年5月29日滬市上還在進(jìn)行交易的全部7只可轉(zhuǎn)換債券的數(shù)據(jù)進(jìn)行實(shí)證分析。

2.轉(zhuǎn)換債券收益率的實(shí)證分析

本文所選取的可轉(zhuǎn)換債券是到2009年5月29日上海證券交易所所有還未到期和未贖回的7只可轉(zhuǎn)換債券的數(shù)據(jù)，數(shù)據(jù)的選取時(shí)間為2008年10月23日-2009年5月31日。收益率采用J .P. Morgan銀行的Risk Metrics方法中運(yùn)用的對(duì)數(shù)收益率:

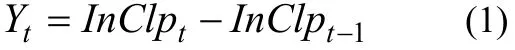
其中， Clpt和Clpt?1分別表示第t天和第t?1天的可轉(zhuǎn)債的收盤(pán)價(jià)， Yt表示第t天的可轉(zhuǎn)債的收益率。

本文所采用的時(shí)間序列模型為ARMA模型和AR? G ARCH 模型[4,5]。ARMA模型也稱為自回歸滑動(dòng)平均模型。 A RMA(p ,q)模型為:

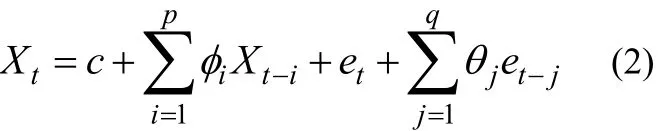
2．1 平穩(wěn)性檢驗(yàn)

由于上述時(shí)間序列模型都是針對(duì)平穩(wěn)的時(shí)間序列而言的，因此我們首先必須對(duì)所選擇的數(shù)據(jù)進(jìn)行平穩(wěn)性檢驗(yàn)。本文采用單位根檢驗(yàn)中的PP檢驗(yàn)來(lái)判別收益率序列的平穩(wěn)性。

首先用SAS軟件對(duì)滬市可轉(zhuǎn)換債券收益率序列}{tY進(jìn)行平穩(wěn)性檢驗(yàn)，其PP檢驗(yàn)的結(jié)果如下：

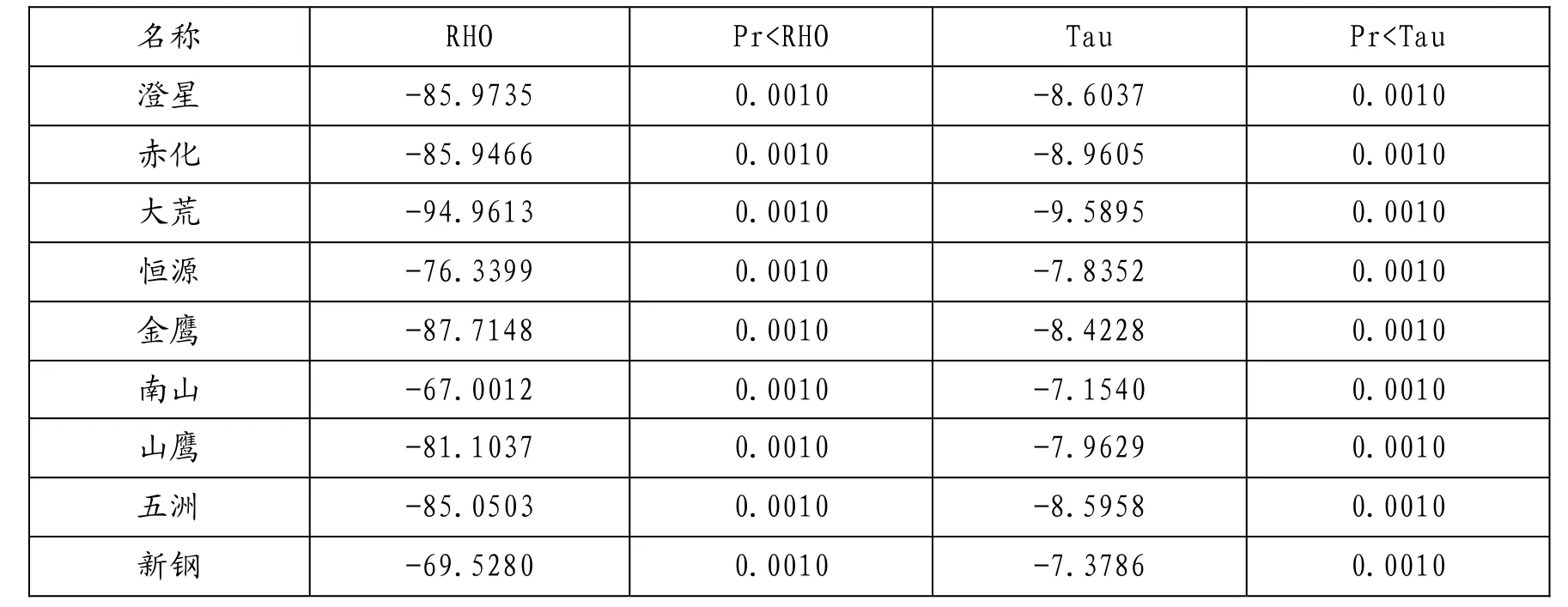
表1.市可轉(zhuǎn)換債券收益率序列}{tY的平穩(wěn)性檢驗(yàn)表

從表一可以看出，由PP統(tǒng)計(jì)量(RHO,Tau)計(jì)算出來(lái)的概率值都為0.0010(<0.01),因此可以認(rèn)為對(duì)數(shù)收益率序列 { Yt} 是平穩(wěn)的。

2.2.型的選擇和參數(shù)估計(jì)

ARMA模型的關(guān)鍵性假設(shè)之一就是誤差的方差保持不變，而 A R? G ARCH 模型的誤差的方差不為常量。因此數(shù)據(jù)的異方差性直接決定著模型的選取。所以下面必須對(duì)可轉(zhuǎn)換債券收益率序列 { Yt} 進(jìn)行異方差性檢驗(yàn)。

表2.市可轉(zhuǎn)換債券收益率序列}{tY的異方差性檢驗(yàn)表

其中表二的LM統(tǒng)計(jì)量漸近服從 χ2(1)分布，并且只顯示了滯后一階的LM統(tǒng)計(jì)量的值及其對(duì)應(yīng)的概率值。

通過(guò)對(duì)表二的數(shù)據(jù)的中的LM統(tǒng)計(jì)量對(duì)應(yīng)的概率值與顯著性水平0.05的比較，可以得到如下結(jié)論：

(1)可轉(zhuǎn)換債券大荒和新鋼的收益率有異方差性，因此可以用異方差模型進(jìn)行擬合；

(2) 其他可轉(zhuǎn)換債券的收益率無(wú)異方差性，因此可以用 A RMA(p ,q)模型進(jìn)行擬合。

下面用SAS軟件對(duì)選取的可轉(zhuǎn)換債券的收益率進(jìn)行 A RMA(p ,q)模型和異方差模型定階和參數(shù)估計(jì),其結(jié)果如下：

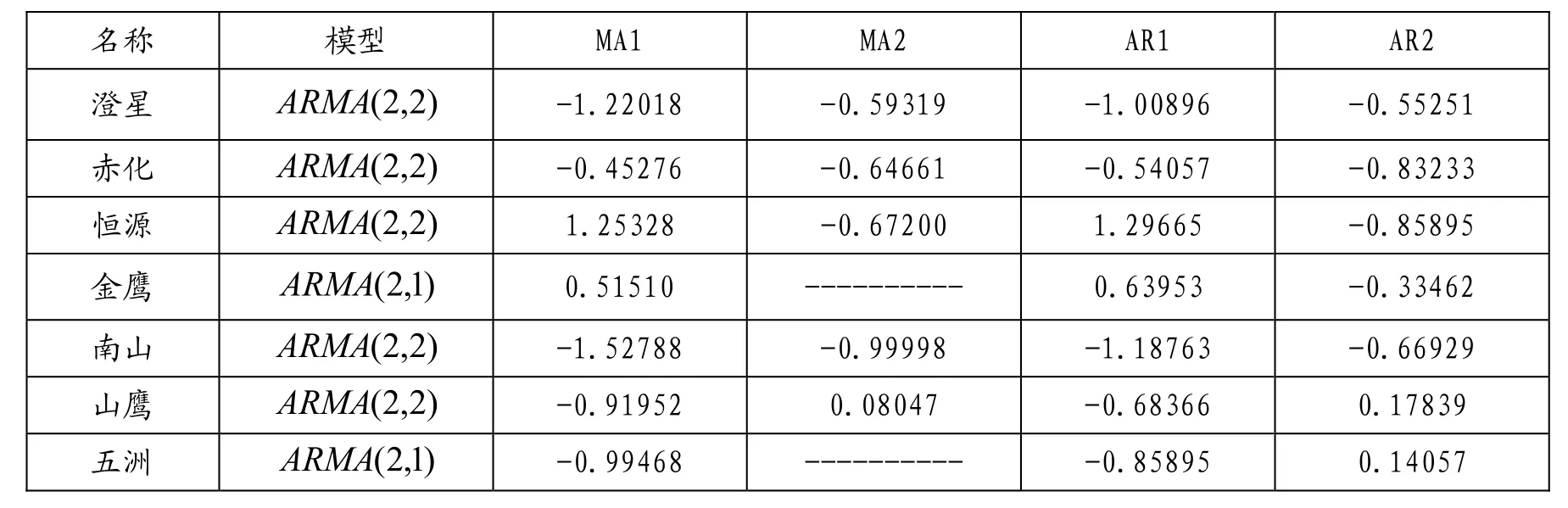
表3.RMA(p ,q)模型參數(shù)估計(jì)

表4.方差 A R (1) ? G ARCH(1,1)模型參數(shù)估計(jì)

其中， A RMA(p,q)模型參數(shù)估計(jì)所使用的方法為極大似然估計(jì)和無(wú)條件最小二乘估計(jì)；異方差模型參數(shù)估計(jì)所使用的方法為極大似然估計(jì)；表三和表四的參數(shù)估計(jì)值都是顯著的。

再分別對(duì) A RMA(p,q)模型和異方差模型的殘差進(jìn)行Q統(tǒng)計(jì)量檢驗(yàn)，其結(jié)果如下：

表5.RMA(p,q)模型的殘差檢驗(yàn)

我們通過(guò)對(duì)表五的第三列數(shù)據(jù)的觀察，發(fā)現(xiàn)Q統(tǒng)計(jì)量對(duì)應(yīng)的概率值均大于顯著性水平0.05，所以可以認(rèn)為：

（1）可轉(zhuǎn)換債券澄星、赤化、恒源、南山、山鷹的對(duì)數(shù)收益率通過(guò))2,2(ARMA模型過(guò)濾后的殘差為白噪聲。

（2）其他的可轉(zhuǎn)換債券的對(duì)數(shù)收益率通過(guò))1,2(ARMA模型過(guò)濾后的殘差為白噪聲。

表6.方差 A R (1) ? G ARCH(1,1)模型的殘差檢驗(yàn)

從表六的 Q統(tǒng)計(jì)量對(duì)應(yīng)的概率值均大于顯著性水平 0.05，所以可以認(rèn)為表中的所有可轉(zhuǎn)換債券的對(duì)數(shù)收益率通過(guò)AR (1) ? G ARCH(1,1)模型過(guò)濾后的殘差為白噪聲。

由此我們可以初步認(rèn)為上述模型是合理的。

2.3.值模擬和分析

利用上面所得到的模型，通過(guò)蒙特卡洛模擬得到未來(lái)7天的收益率與實(shí)際收益率對(duì)比圖如下：

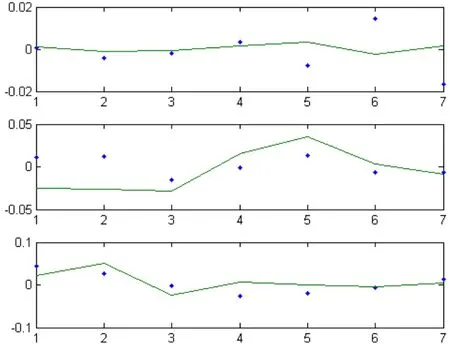
圖1.星、赤化、恒源轉(zhuǎn)債模擬收益率與實(shí)際收益率對(duì)比圖

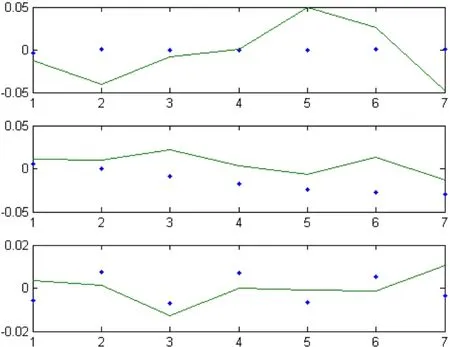
圖2.鷹、南山、山鷹轉(zhuǎn)債模擬收益率與實(shí)際收益率對(duì)比圖

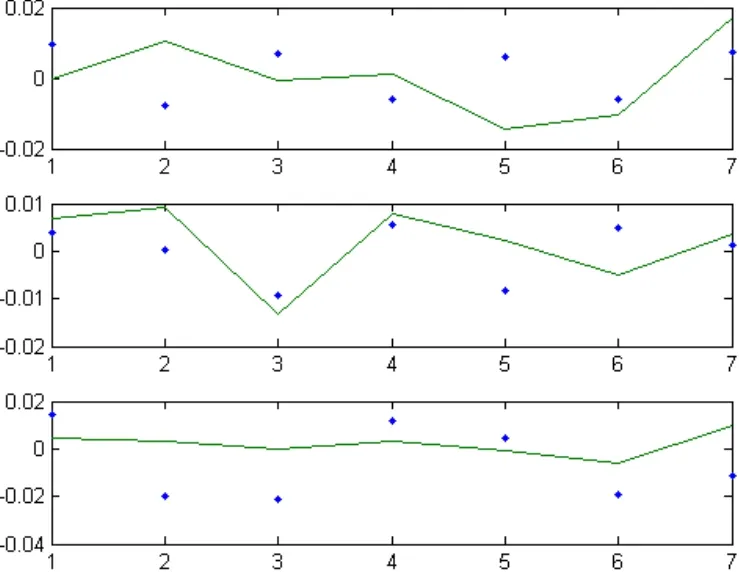
圖3.洲、大荒、新鋼轉(zhuǎn)債模擬收益率與實(shí)際收益率對(duì)比圖

從數(shù)值模擬的圖像可以看出

（1）所有的模擬收益率都在實(shí)際收益率的上下波動(dòng)，說(shuō)明時(shí)間序列模型可以對(duì)可轉(zhuǎn)換債券的收益率進(jìn)行短期的預(yù)測(cè)。

（2）模擬得到的收益率與實(shí)際收益率存在一定的誤差，說(shuō)明得到的模型還是不能反映出實(shí)際收益率的全部變化情況。產(chǎn)生這種情況的原因可能有如下兩種可能：一種是由于得到模型不夠準(zhǔn)確，另一種就是時(shí)間序列模型本身就無(wú)法準(zhǔn)確的描述可轉(zhuǎn)換債券的收益率。

(3) 使用 ARMA模型模擬的可轉(zhuǎn)換債券的收益率體現(xiàn)出的實(shí)際收益率的波動(dòng)性不是很明顯，但是使用異方差模型模擬的兩只可轉(zhuǎn)換債券的收益率更能體現(xiàn)出實(shí)際收益率的波動(dòng)性。

3.束語(yǔ)

由于時(shí)間序列模型在模擬金融資產(chǎn)收益率方面有著廣泛的應(yīng)用，因此本文利用到2009年5月25日滬市還在進(jìn)行交易的可轉(zhuǎn)換債券的收盤(pán)價(jià)對(duì)時(shí)間序列模型在其收益率模擬方面的應(yīng)用進(jìn)行了實(shí)證，結(jié)果發(fā)現(xiàn)對(duì)于可轉(zhuǎn)換債券的收益率的模擬結(jié)果是不能讓人滿意的，這有可能是由于如下三個(gè)原因所致：（1）時(shí)間序列模型不能很好的刻畫(huà)可轉(zhuǎn)換債券包含有期權(quán)的價(jià)值；（2）外界因素（如全球金融危機(jī)，國(guó)家出臺(tái)的重大政策，自然災(zāi)難等）對(duì)金融資產(chǎn)特別是對(duì)可轉(zhuǎn)換債券收益率的影響在時(shí)間序列模型中沒(méi)有很好的體現(xiàn)出來(lái)；（3）我國(guó)證券市場(chǎng)上的可轉(zhuǎn)換債券發(fā)展還不夠完善。

[1]劉立喜.可轉(zhuǎn)換公司債券[M].上海:上海財(cái)經(jīng)大學(xué)出版社，1999.

[2]BrennanM,Schwartz E. Analyzing convertible bonds[J]. Journal of Financial and Quantitative Analysis,15(4): 907- 929., 1980.

[3]Manuel Ammann a, Axel Kind, Christian Wilde. Are convertible bonds underpriced?An analysis of the French market[J].Journal of Banking & Finance 27:635–653, 2003.

[4]James D. Hamilton.Time series analysis[M].Prinston University Press.1994.

[5]Ruey S. Tsay.金融時(shí)間序列分析[M].北京:機(jī)械工業(yè)出版社.2006.4.