基于累積誤差極小值的 SINS初始對(duì)準(zhǔn)＊

吳富梅 楊元喜

（1)解放軍信息工程大學(xué)測(cè)繪學(xué)院,鄭州 450052 2)西安測(cè)繪研究所,西安 710054）

基于累積誤差極小值的 SINS初始對(duì)準(zhǔn)＊

吳富梅1,2)楊元喜2)

（1)解放軍信息工程大學(xué)測(cè)繪學(xué)院,鄭州 450052 2)西安測(cè)繪研究所,西安 710054）

為了在較短的時(shí)間內(nèi)獲得較高的 SI NS初始對(duì)準(zhǔn)精度,提出一種基于累積誤差極小值的初始對(duì)準(zhǔn)方法。首先給出 SI NS力學(xué)編排過(guò)程;然后在此基礎(chǔ)上導(dǎo)出 SI NS導(dǎo)航誤差傳播公式;基于速度誤差和位置誤差公式推導(dǎo)出累積誤差與初始對(duì)準(zhǔn)誤差的關(guān)系,給出基于載體最后靜止時(shí)刻累積誤差極小值的確定初始姿態(tài)角 (航向角)公式。最后用兩組實(shí)測(cè)數(shù)據(jù)對(duì)這種新算法進(jìn)行驗(yàn)證。結(jié)果表明當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較長(zhǎng)時(shí),Kal man濾波精對(duì)準(zhǔn)和基于累積誤差極小值的初始對(duì)準(zhǔn)方法都可以獲得較高精度的對(duì)準(zhǔn)角;當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較短時(shí),Kal man濾波精對(duì)準(zhǔn)精度較低,而基于累積誤差極小值的初始對(duì)準(zhǔn)方法仍可以獲得較高精度的對(duì)準(zhǔn)角。

捷聯(lián)慣性導(dǎo)航系統(tǒng);初始對(duì)準(zhǔn);航向角;誤差極小值;Kalman濾波

1 引言

捷聯(lián)慣性導(dǎo)航系統(tǒng) (SI NS)初始對(duì)準(zhǔn)包括載體位置對(duì)準(zhǔn)和方位對(duì)準(zhǔn)。位置對(duì)準(zhǔn)一般是通過(guò)外界輔助設(shè)備獲得,如由 GPS定位結(jié)果獲得載體初始位置。方位對(duì)準(zhǔn)可以通過(guò)自對(duì)準(zhǔn)或外界輔助設(shè)備對(duì)準(zhǔn)獲得[1],如磁羅盤或多天線 GPS接收機(jī)等。但磁羅盤對(duì)準(zhǔn)精度較低[2],而多天線 GPS接收機(jī)解算復(fù)雜[3,4],因此較高精度 SI NS一般采用自對(duì)準(zhǔn)方式進(jìn)行初始對(duì)準(zhǔn)。初始對(duì)準(zhǔn)誤差是影響 SI NS導(dǎo)航或者GPS/SI NS組合導(dǎo)航精度主要的誤差源,在導(dǎo)航過(guò)程中不易得到正確修正,因此需要嚴(yán)格控制[5,6]。

在捷聯(lián)慣導(dǎo)初始對(duì)準(zhǔn)中,影響航向角對(duì)準(zhǔn)精度的主要因素是陀螺漂移,影響俯仰角和翻滾角對(duì)準(zhǔn)精度的因素是加速度計(jì)偏置。由于陀螺漂移的復(fù)雜性和隨機(jī)性,航向角對(duì)準(zhǔn)一直是初始對(duì)準(zhǔn)中的研究難點(diǎn)[5,7]。初始對(duì)準(zhǔn)包括兩個(gè)階段：粗對(duì)準(zhǔn)和精對(duì)準(zhǔn)。Kalman濾波是最常用的一種精對(duì)準(zhǔn)方法。但Kalman濾波獲得精確估計(jì)的前提是需要可靠的函數(shù)模型、隨機(jī)模型以及足夠的對(duì)準(zhǔn)時(shí)間[7,8]。當(dāng)建立的濾波模型不正確或者模型噪聲方差陣不能反映實(shí)際噪聲時(shí),Kalman濾波的對(duì)準(zhǔn)精度就會(huì)得不到可靠保證甚至濾波會(huì)發(fā)散[9];當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較短時(shí),Kalman濾波也許就不能收斂,這樣姿態(tài)角尤其是航向角的精度就得不到保證[10]。

基于此,本文提出一種基于誤差累積極小值的初始對(duì)準(zhǔn)新方法,有望在較短的對(duì)準(zhǔn)時(shí)間內(nèi)得到較高的對(duì)準(zhǔn)精度。

2 SINS力學(xué)編排和誤差分析

SI NS導(dǎo)航系統(tǒng)是通過(guò)力學(xué)編排過(guò)程將陀螺儀和加速度計(jì)觀測(cè)得到的旋轉(zhuǎn)角增量和速度增量轉(zhuǎn)化為載體運(yùn)動(dòng)過(guò)程中的位置和速度[11]：

1)計(jì)算載體坐標(biāo)系至導(dǎo)航坐標(biāo)系的轉(zhuǎn)換矩陣

選取地固坐標(biāo)系 (WGS84)為導(dǎo)航坐標(biāo)系。通過(guò)陀螺儀測(cè)得的角度變化率扣除地球自轉(zhuǎn)角速度經(jīng)過(guò)四元數(shù)的更新[11],可以得到載體坐標(biāo)系至導(dǎo)航坐標(biāo)系的轉(zhuǎn)換矩陣那么載體坐標(biāo)系至當(dāng)?shù)厮阶鴺?biāo)系(東北天坐標(biāo)系)的轉(zhuǎn)換矩陣為:

2)計(jì)算載體的位置和速度

由加速度計(jì)測(cè)得的是采樣間隔Δt里載體坐標(biāo)系中相應(yīng)于比力的速度增量,需要通過(guò)轉(zhuǎn)換矩陣轉(zhuǎn)換成導(dǎo)航坐標(biāo)系中的速度增量:

那么,載體的速度增量為[7,8]

經(jīng)過(guò)積分,載體的速度和位置分別為:

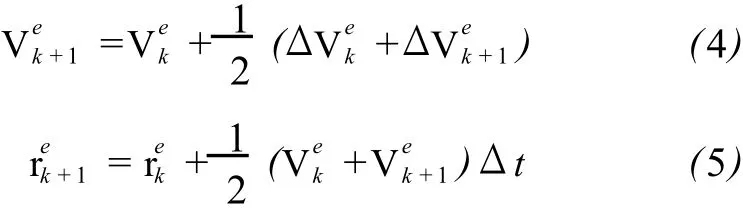
3)誤差分析

對(duì)式(3)微分,可得載體速度增量的誤差:

其中,Ω為真實(shí)轉(zhuǎn)換矩陣與計(jì)算的轉(zhuǎn)換矩陣之間失準(zhǔn)角誤差ε的反對(duì)稱陣,為加速度計(jì)觀測(cè)誤差,δVe為由當(dāng)前速度引起的誤差,δ γe為正常重力向量誤差。

位置增量誤差為

其中,δ是積分誤差。

3 基于累積誤差極小值的 SINS初始對(duì)準(zhǔn)

在獲得精度較高的姿態(tài)角之前,需要通過(guò)粗對(duì)準(zhǔn)獲得載體的粗略姿態(tài)角[12]：

1)粗對(duì)準(zhǔn)

重力加速度 g和地球自轉(zhuǎn)角速度ωie在當(dāng)?shù)厮阶鴺?biāo)系(東北天坐標(biāo)系)中的各分量分別為：

其中,B為地理緯度。

由 gL叉乘可構(gòu)成一個(gè)新向量γL,即:

靜基座下載體坐標(biāo)系中,理想情況時(shí)陀螺儀和加速度計(jì)的輸出信號(hào)是和 gb,由和 gb叉乘也可得到γb,根據(jù)姿態(tài)矩陣可得到:

如此可獲得 3個(gè)姿態(tài)角 y、p和 r的概略值。

因?yàn)橥勇輧x和加速度計(jì)的輸出信號(hào)包含陀螺漂移、加速度計(jì)偏置以及各種其他誤差源的干擾,粗對(duì)準(zhǔn)獲得姿態(tài)角誤差較大,因此需要對(duì)粗對(duì)準(zhǔn)結(jié)果進(jìn)行精確校正。Kalman濾波算法是最常用的一種精對(duì)準(zhǔn)方法[7,8],但是應(yīng)用這種算法需要有足夠的對(duì)準(zhǔn)時(shí)間(不少于 5分鐘)和可靠的狀態(tài)噪聲和觀測(cè)噪聲矩陣。當(dāng)這兩個(gè)前提得不到滿足時(shí),Kalman濾波獲得高精度對(duì)準(zhǔn)結(jié)果就很難保證,尤其是對(duì)準(zhǔn)時(shí)間少于 5分鐘時(shí),Kalman濾波結(jié)果也許就不會(huì)收斂。

初始對(duì)準(zhǔn)俯仰角和翻滾角主要受加速度偏置影響,在 Kal man濾波精對(duì)準(zhǔn)過(guò)程中,收斂速度較快;而航向角主要受陀螺漂移影響,收斂速度較慢,在較短的時(shí)間內(nèi)很難獲得高精度的對(duì)準(zhǔn)精度。因此下面主要針對(duì)對(duì)準(zhǔn)時(shí)間較短、初始航向角誤差較大的情況,提出一種精對(duì)準(zhǔn)方法。

2)基于累積誤差極小值的精對(duì)準(zhǔn)

由分析可知,式 (9)中Ω失準(zhǔn)角誤差矩陣包含兩個(gè)方面的誤差：初始對(duì)準(zhǔn)誤差ε1和開始?xì)v元到當(dāng)前歷元的累積誤差ε2,其反對(duì)稱陣分別為Ω1、Ω2。

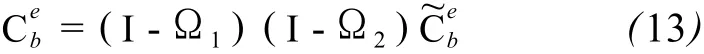
總誤差ε的反對(duì)稱矩陣為:

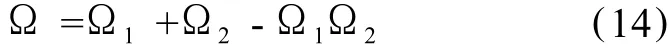
在載體 SI NS導(dǎo)航過(guò)程中,若采用 GPS對(duì) SI NS誤差進(jìn)行周期性校正,則可忽略速度誤差δVe、正常重力誤差δ γe和積分誤差δ的影響。則載體速度和位置誤差主要與姿態(tài)角誤差以及加速度計(jì)觀測(cè)誤差有關(guān),即：

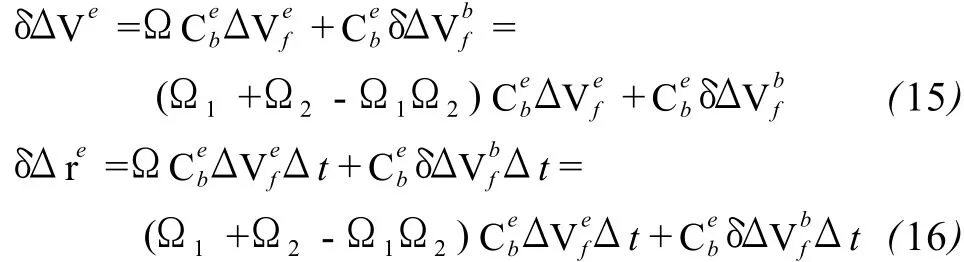
如果Ω1=0,即初始對(duì)準(zhǔn)無(wú)誤差,則速度和位置誤差主要與導(dǎo)航過(guò)程中姿態(tài)角累積誤差和加速度計(jì)觀測(cè)誤差有關(guān)。對(duì)于精度較高的 SI NS系統(tǒng),在較短的時(shí)間里這兩項(xiàng)誤差影響比較小而且具有隨機(jī)性。

如果Ω1≠0,即初始對(duì)準(zhǔn)存在誤差(主要為航向角誤差),初始對(duì)準(zhǔn)角度誤差和 SI NS導(dǎo)航過(guò)程中累積的姿態(tài)角誤差會(huì)一直影響整個(gè) SI NS導(dǎo)航過(guò)程,而且隨著時(shí)間增長(zhǎng)與Ω2增大,Ω2-Ω1Ω2的影響也會(huì)越來(lái)越大。但是這種誤差具有較強(qiáng)的規(guī)律性,而且會(huì)直接反映到載體最后靜止時(shí)刻位置和速度的誤差上(理想狀況下誤差真值為 0)。因此可以通過(guò)檢測(cè)SI NS最后靜止時(shí)刻的導(dǎo)航誤差來(lái)確定載體的初始航向角。圖 1給出了不同的初始航向角對(duì) SI NS單獨(dú)導(dǎo)航結(jié)果的影響 (9.6°為正確值)。從圖 1中可以看出：(1)當(dāng)載體處于初始靜止時(shí)刻,由于系統(tǒng)尚不穩(wěn)定,不能用初始靜止時(shí)刻的誤差作為檢測(cè)的標(biāo)準(zhǔn);(2)當(dāng)載體處于最后靜止時(shí)刻,航向角誤差影響較大,并且呈線性增大;(3)航向角在載體運(yùn)動(dòng)時(shí)刻也有影響,但是由于載體運(yùn)動(dòng)的復(fù)雜性,誤差不能表現(xiàn)出規(guī)律性。因此,可以針對(duì)航向角誤差對(duì)導(dǎo)航誤差影響的特點(diǎn)(2)作為確定初始航向角的條件。

假定粗對(duì)準(zhǔn)航向角為 y0,真實(shí)航向角在區(qū)間[y0-θ°,y0+θ°]之間,取 y1=y0-θ°,yk+1=yk+α2θ°,當(dāng)

yk就作為真實(shí)初始航向角的估計(jì)值。

對(duì)這種初始對(duì)準(zhǔn)方法進(jìn)行分析可知:

1)該方法是一種在事后重新確定初始航向角的方法,適合于事后高精度數(shù)據(jù)處理,在實(shí)時(shí)導(dǎo)航時(shí)不適用;

2)為了得到較高的對(duì)準(zhǔn)精度,需要較高精度的SI NS系統(tǒng)。

4 算例與分析

采用兩組 GPS/I NS組合導(dǎo)航數(shù)據(jù)對(duì)上述初始對(duì)準(zhǔn)方法進(jìn)行驗(yàn)證。

算例 1：取一組 GPS/I NS車載導(dǎo)航數(shù)據(jù)。I MU采樣頻率為 100 Hz,GPS數(shù)據(jù)采樣周期為 1.0 s,組合周期為 1.0 s。載體初始靜止時(shí)間約 5分鐘。初始位置 X、Y、Z坐標(biāo)分別為 -2 271 358.223 m、5 008 107.342 m、3 220 377.609 m。

算例 2：取一組 GPS/I NS機(jī)載導(dǎo)航數(shù)據(jù)。I MU采樣頻率為 200 Hz,GPS數(shù)據(jù)采樣周期為 1.0 s,組合周期為 1.0 s。載體初始靜止時(shí)間約 2分鐘。初始位置 X、Y、Z坐標(biāo)分別為 4 275 902.267 m、649 200.954 m、4 672 778.929 m。

算例中,θ=5°,α=0.01。下列參數(shù)由經(jīng)驗(yàn)確定：陀螺儀和加速度計(jì)誤差相關(guān)時(shí)間分別為 600 s與 600 s;陀螺儀和加速度計(jì)初始均方差分別取 10. 0°/h和100μg;初始位置誤差為5 m、5 m、7 m;初始速度誤差為 0.1 m/s;初始平臺(tái)失準(zhǔn)角誤差分別為100.0 s、100.0 s和 500.0 s;采用松組合方式導(dǎo)航,觀測(cè)量初始方差取 1 m2和 0.01 m2/s2。

采用兩種方案進(jìn)行初始對(duì)準(zhǔn)：

方案 1：Kaman濾波初始對(duì)準(zhǔn);

方案 2：基于累積誤差極小值的初始對(duì)準(zhǔn);

圖 2和圖 3給出算例 1中利用 2分鐘靜止數(shù)據(jù)由方案 1給出的初始對(duì)準(zhǔn)結(jié)果。圖 4和圖 5給出算例 1中利用 5分鐘靜止數(shù)據(jù)由方案 1給出的初始對(duì)準(zhǔn)結(jié)果。圖 6給出了算例 1方案 2最后靜止時(shí)刻X、Y、Z方向的位置、速度誤差以及總誤差隨不同初始航向角的變化圖。表 1給出了這兩種方案初始對(duì)準(zhǔn)的最后結(jié)果。

圖 2 算例 1,方案 1,初始對(duì)準(zhǔn)航向角(2分鐘)Fig.2 Initial yaw of scheme 1 from data 1(two minutes)

圖 3 算例 1,方案 1,初始對(duì)準(zhǔn)俯仰角和翻滾角(2分鐘)Fig.3 Initial pitch and roll of scheme 1 from data 1(t wo minutes)

圖 4 算例 1,方案 1,初始對(duì)準(zhǔn)航向角(5分鐘)Fig.4 Initial yaw of scheme 1 from data 1(five minutes)

圖 5 算例 1,方案 1,初始對(duì)準(zhǔn)俯仰角和翻滾角(5分鐘)Fig.5 Initial pitch and roll of scheme 1 from data 1(five minutes)

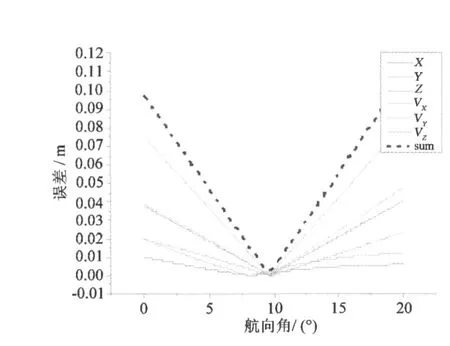
圖 6 算例 1,方案 2,初始對(duì)準(zhǔn)航向角(2分鐘)Fig.6 Initial yaw of scheme 2 from data 1(two minutes)

圖 7 算例 2,方案 1,初始對(duì)準(zhǔn)航向角(2分鐘)Fig.7 Initial yaw of scheme 1 from data 2(two minutes)

表 1 算例 1,兩種方案初始對(duì)準(zhǔn)姿態(tài)角Tab.1 I n itial attitude angles of two schemes from data 1

圖 7和圖 8給出了算例 2方案 1利用 2分鐘靜止數(shù)據(jù)初始對(duì)準(zhǔn)結(jié)果。圖 9給出了算例 2方案 2最后靜止時(shí)刻 X、Y、Z方向的位置、速度誤差以及總誤差隨不同初始航向角的變化。

圖 8 算例 2,方案 2,2分鐘初始對(duì)準(zhǔn)俯仰角和翻滾角Fig.8 Initial attitude angles of scheme 2 from data 2(two unites)

圖 9 算例 2,方案 2,2分鐘初始對(duì)準(zhǔn)航向角Fig.9 Initial yaw of scheme 2 from data 2(two minutes)

表 2 算例 2,兩種方案初始對(duì)準(zhǔn)姿態(tài)角Tab.2 I n itial attitude angles of two schemes from data 2

由計(jì)算結(jié)果可以得出：

1)由于受陀螺漂移的影響,航向角初始對(duì)準(zhǔn)需要較長(zhǎng)時(shí)間,Kal man濾波收斂速度較慢;而俯仰角和翻滾角主要受加速度偏置影響,初始對(duì)準(zhǔn)時(shí)間較短,Kalman濾波收斂速度較快;因此當(dāng)載體初始初始對(duì)準(zhǔn)時(shí)間較短時(shí),利用 Kalman濾波初始對(duì)準(zhǔn),主要會(huì)影響航向角的精度,而俯仰角和翻滾角受到的影響較小;

2)當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較長(zhǎng)且狀態(tài)噪聲矩陣可靠時(shí),由 Kalman濾波對(duì)準(zhǔn)可以獲得較高的對(duì)準(zhǔn)精度;

3)由圖 2和圖 7可知,當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較短時(shí),Kal man濾波對(duì)準(zhǔn)過(guò)程中航向角對(duì)準(zhǔn)精度較低,而俯仰角和翻滾角對(duì)準(zhǔn)精度較高;

4)當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較短時(shí),基于累積誤差極小值的初始對(duì)準(zhǔn)方法通過(guò)檢測(cè)載體最終靜止時(shí)刻的位置、速度以及總誤差的局部極小值,可以獲得精度較高的航向角。

5)由圖 6可看出,由于殘留誤差影響,位置、速度以及總誤差的極小值不會(huì)完全一致,這時(shí)取總誤差極小點(diǎn)時(shí)的航向角為載體初始航向角。

5 結(jié)論

在 SI NS初始對(duì)準(zhǔn)過(guò)程中,當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較長(zhǎng)且濾波噪聲矩陣可靠時(shí),可以通過(guò) Kalman濾波獲得精度較高的初始姿態(tài)角;當(dāng)載體初始對(duì)準(zhǔn)時(shí)間較短時(shí),通過(guò) Kalman濾波可以獲得較高精度的俯仰角和翻滾角,但是由于受到陀螺漂移誤差的影響,航向角收斂速度較慢,對(duì)準(zhǔn)精度較低;基于累積誤差極小值的初始對(duì)準(zhǔn)方法,可以在較短的時(shí)間里獲得較高精度的航向角。

1 Godha S.Perfor mance evaluation of low cost MEMS-based MU integrated with GPS for land vehicle navigation application[D].Depart ment of Geomatics Engineering,University of Calgary,Canada,2006.

2 Wang J H.IntelligentMEMS I NS/GPS integration for land vehicle navigation[D].Department of Geomatics Engineering,University of Calgary,Canada,2006.

3 GangLu.Development of a GPSmulti-antenna system for attitude deter mination[D].Departmentof Geomatics Engineering,University of Calgary,Canada,1995.

4 Ji m S.Development of a multi-sensor GNSS-based vehicle navigation system[D].Department of Geomatics Engineering,University of Calgary,Canada,2000.

5 萬(wàn)德鈞,房建成.慣性導(dǎo)航初始對(duì)準(zhǔn)[M].南京：東南大學(xué)出版社,1998.(Wan Dejun and Fang Jiancheng.I NS initial alignment[M].Nanjing：Southeast University Press, 1998)

6 袁信,俞濟(jì)祥,陳哲.導(dǎo)航系統(tǒng)[M].北京：航空工業(yè)出版社,1992.(Yuan Xin,Yu Jixiang and Chen Zhe.Navigation system[M].Beijing：Astronautics Industry Press,1992)

7 秦永元.卡爾曼濾波與組合導(dǎo)航原理[M].西安：西北工業(yè)大學(xué)出版社,1998.(Qin Yongyuan.Kalman filtering and integrated navigation[M].Xi’an：Northwestern Polytechnical University Press,1998)

8 朱利鋒,鮑其蓮,張炎華.捷聯(lián)慣導(dǎo)系統(tǒng)初始對(duì)準(zhǔn)的 H濾波及卡爾曼濾波比較研究 [J].中國(guó)慣性技術(shù)學(xué)報(bào), 2005,13(3)：4-9.(Zhu Lifeng,Bao Qilian and Zhang Yanhua.Comparison of Kalman filter and H filter for initial alignment of SI NS[J].Journal of Chinese Inertial Technology,2005,13(3)：4-9)

9 Yang Yuanxi,Xu Tianhe and He Haibo.On adaptively kinematic filtering[J].Selected Papers in English of Acta Geodetica et Cartographica Sinica,2001,25-32.

10 聶莉娟.捷聯(lián)慣導(dǎo)系統(tǒng)初始對(duì)準(zhǔn)濾波技術(shù)研究[D].哈爾濱工程大學(xué),2004.(Nie Lijuan.The research of filter technic in inertial alignment of strapdown system[D].Harbin EngineeringUniversity,2004)

11 董緒榮,張守信,華仲春.GPS/I NS組合導(dǎo)航定位及其應(yīng)用[M].長(zhǎng)沙：國(guó)防科技大學(xué)出版社,1998.(Dong Xurong,Zhang Shouxin and Hua Zhongchun.GPS/I NS integration navigation positioning and it’s application[M]. Changsha：National Defence Science and Technology University Press,1998)

12 吳富梅,楊元喜.基于小波變換和序貫抗差估計(jì)的捷聯(lián)慣導(dǎo)初始對(duì)準(zhǔn)[J].武漢大學(xué)學(xué)報(bào)(信息科學(xué)版),2007, 32(7)：617-620.(Wu Fumei and Yang Yuanxi.SI NS initial alignment based onwavelet transform and sequential robust adjustment[J].Geomatics and Information Science of Wuhan University,2007,32(7)：617-620)

A NEW M ETHOD OF SINS INITIAL AL IGNM ENT BASED ONM INIM UM OF CUM ULATED ERROR

Wu Fumei1,2)and Yang Yuanxi2)

(1)Institute of Surveying and M apping,Infor m ation Engineering University,Zhengzhou 450052 2)Xi’an Research Institute of Surveying and M apping,Xi’an 710054)

A new method of SI NS initial alignment based on the mini mum of cumulated error is presented for the situation of short time for initial alignment.Firstly,the mechanization and the error for mulas of SI NS are given. Further more the relation between attitude angles and cumulated errors are deduced based on position error and velocity error for mulas,and the principle of fixing initial yaw angle based on cumulated error checking is given.Finally,two real experiments are carried out to show thatwhen the initial static time is long enough,Kal man filtering and the new method can both bring about good results;butwhen the initial static time is very short,Kalman filtering can not obtain accurate yaw angle while the new method is able to fix the accurate yaw angle.

SI NS;initial alignment;yaw;minimum of cumulated error;Kalman filtering

1671-5942(2010)05-0129-06

2010-04-09

國(guó)家自然科學(xué)基金(40774001);國(guó)家 863計(jì)劃項(xiàng)目(2007AA12Z331);衛(wèi)星導(dǎo)航與定位教育部重點(diǎn)實(shí)驗(yàn)室(B類)開放基金;信息工程大學(xué)博士研究生創(chuàng)新基金

吳富梅,女,1981年生,博士,主要從事動(dòng)態(tài)大地測(cè)量數(shù)據(jù)處理.E-mail：wfm8431812@163.com

P207;P203

A