關于Finsler遞歸定理的幾點注記

燕子宗，尹 飛

(長江大學信息與數學學院，湖北 荊州 434023)

關于Finsler遞歸定理的幾點注記

燕子宗，尹 飛

(長江大學信息與數學學院，湖北 荊州 434023)

Finsler遞歸定理和S-引理，是二次約束二次優化問題的2個基本結果。它們以及由Finsler遞歸定理發展起來的雙邊投影定理在魯棒優化和控制領域扮演十分重要的角色。利用二次函數的連通特性證明了Finsler遞歸定理和S-引理的等價性，并給出了雙邊投影定理的一個新證明。

Finsler遞歸定理；S-引理；雙邊投影定理

Finsler遞歸定理主要有以下2個結果。

定理1[1]設A，B是n階對稱矩陣且B是不定的，則存在t∈R使得A+tB半正定當且僅當：

xTBx=0?xTAx≥0

(1)

定理2[1](嚴格Finsler遞歸定理) 設A,B是n階對稱矩陣,則存在t∈R使得A+tB正定當且僅當：

x≠0xTBx=0?xTAx≥0

(2)

作為S-過程的最早結果，Finsler遞歸定理有很長的歷史并被重新證明多次[2]。由定理2發展起來的雙邊投影定理，在控制論的穩定性分析中發揮重要作用[3,4]。S-過程處理多個二次約束下二次優化的可解性問題。1971年，Yakubovich[5]對單個二次約束下二次優化的可解性給出了如下S-引理。

定理3[5](S-引理) 設A和B是對稱實矩陣，二次不等式：

xTAx≥0

(3)

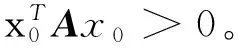
xTBx≥0

(4)

成立的充分必要條件是存在非負常數λ≥0使得B-λA半正定。

下面，筆者將證明定理1與S-引理的等價性，并給出了雙邊投影定理的一個新證明。

1 Finsler遞歸定理與S-引理的等價性

在對定理1和定理3等價性證明之前，首先對齊二次映射構成的錐給出一個連通性結果。為了敘述方便，引入記號：

(5)

代表由實對稱矩陣A∈Rn×n確定的二次錐，使用記號0(A)分別代表集合(A)所有內點構成的集合。

引理1設A∈Rn×n為對稱矩陣，則集合(A)-{0}至多由2個連通區域構成。

證明當A半正定時，(A)為全空間Rn,(A)-{0}僅包含一個連通區域。當-A半正定時，(A)為原點集合，因此(A)-{0}為空。以下討論A是不定的情況。不妨假定A是對角矩陣且對角元素為1，-1或者0，因此二次錐(A)可以表示為如下形式：

(6)

式中，1≤klt;m≤n。

若k=1，由錐優化理論[6]可以知道，(A)由2個關于原點對稱的2個二階錐構成，于是結論成立。

若kgt;1，令x2=…=xk-1=0和xk=1，則二次錐(A)包含一個連通子集：

下面給出定理1和定理3的等價性證明。

(1)定理1?定理3。

不妨設B是不定矩陣，由定理3的假設可以得到A也是不定矩陣。由定理1知，存在實數t使得B+tA半正定。另一方面，由定理3的假設知，若x1?0(-B)，則x1?0(-A)。這一事實說明當t≥0時，B+tA不可能半正定，因此tlt;0。此外，若B是半正定矩陣，當然t可以等于0。于是引理1得證。

(2)定理3?定理1。

定理1假設蘊涵如下包含關系：

(7)

2 雙邊投影定理的新證明

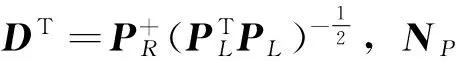
μPTP-Hgt;0

(8)

當且僅當：

(9)

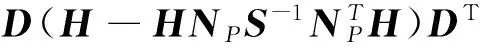
引理3[3](Gahinet-Apkarian) 設A∈Sn是對稱矩陣，且具有3×3分塊。則存在矩陣X使得：

(10)

當且僅當：

(11)

引理2和引理3的證明參見文獻[7,8]

Iwasaki-Skelton，Gahinet-Apkarian各自獨立的獲得了如下雙邊投影定理，它是定理2的一個新擴展。下面給出雙邊投影定理及其一個新的證明。

定理4設H∈Sn是對稱矩陣，P，Q是適當維數矩陣，NP和NQ分別是由核空間N(P)和N(Q)的任意一組基作為列向量構成的矩陣，則存在矩陣X使得：

H+PTXTQ+QTXPlt;0

(12)

當且僅當：

(13)

證明必要性顯然，下證充分性。設V1是N(P)∩N(Q)的一組基作為列向量構成的矩陣，將其分別擴充為N(P)和N(Q)的一組基，記擴充的列向量構成的矩陣記為V2和V3，即：

R(V1，V2)=N(P)R(V1，V3)=N(Q)

這里R(·)代表由矩陣的列向量構成的線性空間。由線性代數知識得到，V1，V2和V3的列向量構成N(P)⊕N(Q)的一組基。令V=(V1，V2，V3)，則V列滿秩。

取R(P)∩R(Q)一組基作為列向量構成矩陣A，則：

P+PA=Q+QA=A

或者等價地，有：

ATP+P=ATQ+Q=AT

顯然AT的核空間N(AT)=N(P)⊕N(Q)。令X1=(QT)+AATP+，則有：

由V的構造知，PV=(O，O，PV3)，QV=(O，QV2，O)，因此有：

由引理3知，在條件(13)的假定下，存在Y使得：

(14)

其中：

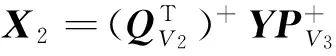
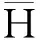
3 結 語

雙邊投影定理3的證明是對Gahinet-Apkarian給出證明的一種修改，該證明同時應用了引理2和引理3。這2個引理都是定理4的特殊形式。例如在定理4中令P=Q可得引理2，若令：

P=(O，O，I)Q=(O，I，O)

則有：

將其分別代入到式(12)和式(13)中就可以得到式(10)和式(11)，即得引理3。

[2]Uhlig F.Onaffine scaling algorithm about pairs of quadratic forms and exetnsions:A survey[J].Linear Algbra Appl,1979,25:219～237.

[3]Gahinet P,Apkarian P.A linear matrix inequality approach toH∞control[J].Int J Robust and Nonlinear Control,1994,(4):421～448.

[4]Iwasaki T,Skelton R E.All controllers for the generalH∞control problem:LMI existence conditions and state space formulas[J].Automatica,1994,30(8):1037～1317.

[5]Yakubovich V A.S-procedure in nonlinear control theory[J].Vestnik Leningrad Univ,1971,(1):62～77.

[6]Ben-Tal A，Nemirovski A.Lectures on Modern Convex Optimization: Analysis,Algorithms and Engineering Applications[A].MPS-SIAM Series on Optimization[C].2001.

[7]黃琳.穩定性與魯棒性的理論基礎[M].北京：科學出版社，2003.

[8]俞立.魯棒控制：線性矩陣不等式處理方法[M].北京：清華大學出版社，2002.

[編輯] 洪云飛

O177.91;O224

A

1673-1409(2010)01-N021-03