用BP神經網絡提高鋰離子電池化成系統采樣精度

吳免利，李劼，肖昕，鄒忠

(1. 中南大學 冶金科學與工程學院，湖南 長沙，410083；2. 中南大學 信息科學與工程學院，湖南 長沙，410083)

在電池化成過程中，對充放電電壓和電流的要求都非常嚴格，過充電會造成鋰離子在負極堆積形成枝晶，刺穿隔膜，形成內部短路，對電池的內部材料造成不可逆影響，降低電池使用壽命，嚴重時會造成電池熱失控而爆炸，對生產造成很大的損害[1?5]。不準確的電流和電壓不利于鋰離子動力電池的分選和配組，使得配組后的單體電池差異性較大，嚴重縮短電池組的使用壽命[6]。湖南中大業翔公司自行研制的YX-20A型鋰離子動力電池化成檢測設備，由于使用較多的非線性元件使得采樣信號和實際的測量值之間存在較大誤差。如果單從硬件上改進，會增加硬件成本，因此，研究一種合適的方法對數據進行修正，來提高系統采樣精度是非常必需的。經實驗證實，用普通的線性回歸模型校正采樣數據，對提高電壓采樣精度有較好的效果，但對提高電流精度效果不佳。人工神經網絡(Artificial neural network, ANN)算法可以在對被測對象不完整或不確定認識的基礎上表示任意非線性關系，因此，為解決上述采樣數據失真問題提供了一種思路。目前神經網絡模型多達幾十種，其中，最典型的就是 BP神經網絡。此網絡具有結構簡單、訓練算法理論依據可靠、推導嚴謹且易于實現、預測能力強等特點[7?10]。為了提高系統充放電控制和采樣精度，本文作者利用 BP神經網絡對非線性系統的學習能力校正系統誤差，并提高控制精度。

1 誤差分析

YX-20A型鋰離子動力電池化成系統的電源控制采用脈沖寬度調制(PWM)的調制方式，在主控器向電源控制板傳輸電壓電流基準后，控制板上的PWM控制芯片TL494將根據采樣的電池電壓或電流控制功率板上 MOS管的開關，從而調節充放電電流。功率板的電路圖如圖1所示，包括MOS管控制電路和檢測回路。

圖1中的MOS管、電感、電容和TL494一起組成PWM電源調節電路，通過調節TL494的占空比調節回路中的電壓和電流。但這些器件都屬于非線性元件，經調節后回路中電池的電壓和電流與設定基準存在一定的偏差，同時，由于化成柜在充放電階段會將大量電能以電阻發熱形式釋放，因此，作為電流檢測的康銅絲電阻，在較高的溫度下也存在一定的非線性特征，造成采集數據失真。PWM 調節電路工作時產生的高頻脈沖也對系統的精度產生較大的影響。

在數據采樣上，電壓誤差都在1.5%左右波動，用普通的線性回歸模型校正采樣電壓可以取得理想的效果。而電流的誤差大于 5%，且波動較大，用同樣的線性方法對采樣電流進行校正，效果并不佳。電流采樣誤差過大會降低 TL494芯片調節的精度，在 10～40 ℃的測試結果表明：PWM轉換過程中電流最大相對誤差為 24%，平均相對誤差約為6.4%。

2 模型建立和數據處理

2.1 BP神經網絡模型的建立

BP網絡是通過將網絡輸出誤差反饋回傳對網絡參數進行修正，從而實現網絡的映射。具有1個隱含層的三層 BP網絡可以有效地逼近任意連續函數。考慮到實際應用的要求，網絡設計時盡可能地減小系統的規模和復雜性，同時考慮到設備周圍環境溫度對硬件性能的影響，本文作者采用2-q-1 型三層BP網絡，即具有2個節點的輸入層、具有q個節點的隱含層和具有1個節點的輸出層。輸入層分別輸入A/D轉換后的電流和環境溫度；輸出層為校正后的電流，隱含層的節點個數q通過實驗的方法確定。

傳統的 BP神經網絡是一種簡單的最速下降靜態尋優方法，在修正權值和閾值時，只按照當前的負梯度方向進行修正，而沒有考慮到以前積累的經驗，即以前時刻的梯度方向，從而使學習過程發生振蕩，收斂緩慢。因此，采用常用的改進算法——動量梯度下降法和L-M(Levenberg-Marquardt)算法對BP神經網絡進行對比訓練。

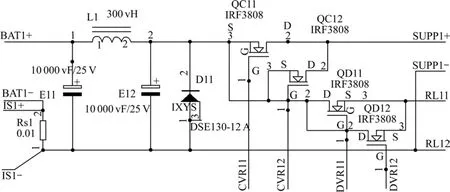
圖1 功率板電路圖Fig.1 Circuit diagram of power board

動量梯度下降法的具體做法是：將上一次權值和閾值調整量的一部分迭加到按本次誤差計算所得的權值和閾值調整量上，作為本次的實際權值和閾值調整量，即

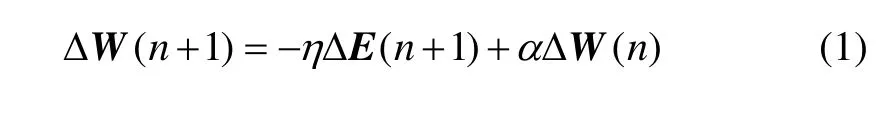
其中：α為動量系數；η為學習率。

對于第p個樣本，在本模型中L-M算法的權值和閾值調整量為：

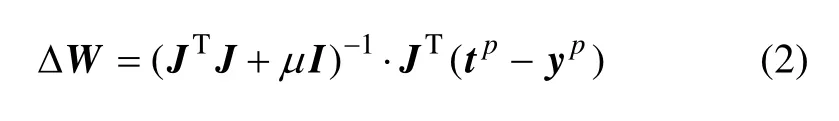
其中：J為網絡誤差對權值和閾值導數的Jacobian矩陣；μ為比例系數，tp為期望輸出；yp為輸出向量。

隱含層中的激勵函數取Sigmoid函數，即

輸出層中的激勵函數取線性函數，即

對于隱含層節點的選取，有如下經驗公式：

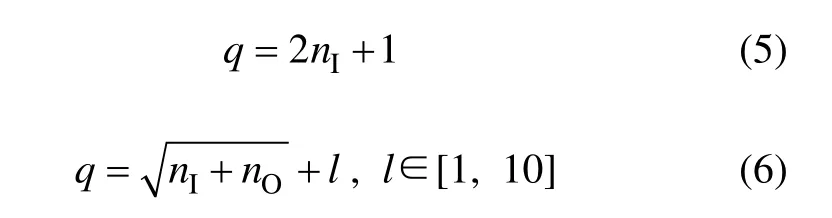
其中：nI為輸入層節點數；nO為輸出層節點數；q為隱含層節點數。

根據這2個經驗公式確定q的取值范圍，然后，通過實驗對比確定合適的q。選取q為3～11范圍內的9個節點進行對比實驗來確實理想的q。訓練時設定最大訓練步數為10萬步，誤差精度為0.000 1。

2.2 樣本的選擇

在不同的環境溫度下，上位機對設備設定由低到高的不同電流基準，當系統運行時，在回路上測量通過電池的實際電流，同時記錄當前的A/D轉換值。將環境溫度和不同設定基準測得的A/D轉換值作為神經網絡的輸入；將回路上實際測量得到的電流轉換到與A/D采樣值相同的度量模式下，作為神經網絡系統的輸出對神經網絡進行訓練。

化成柜的工作狀態有恒流充電、恒流放電、恒壓充電、擱置和循環5類，其中：循環是前4種工步的組合；在擱置狀態下，充放回路是斷開的，電路中只有細小的電流。對恒流充電、恒流放電、恒壓充電分開進行訓練。本文僅以恒流充電為例進行說明。電池化成車間的工作溫度一般為10～40 ℃，鋰離子動力電池的恒流充電階段電流一般為1～10 A。所以，在10～40 ℃(溫度誤差為±1 ℃)選取1～10 A的點進行訓練，積累典型樣本，表1所示為1個典型樣本在不同溫度下的電流。

訓練數據的相對誤差如圖2所示。由圖2可以看出：在不同溫度下，電流的A/D轉換值與真實值的誤差波動都較大，最大波動幅度可達 5%，并且規律性不確定，表明訓練數據的非線性特征明顯。

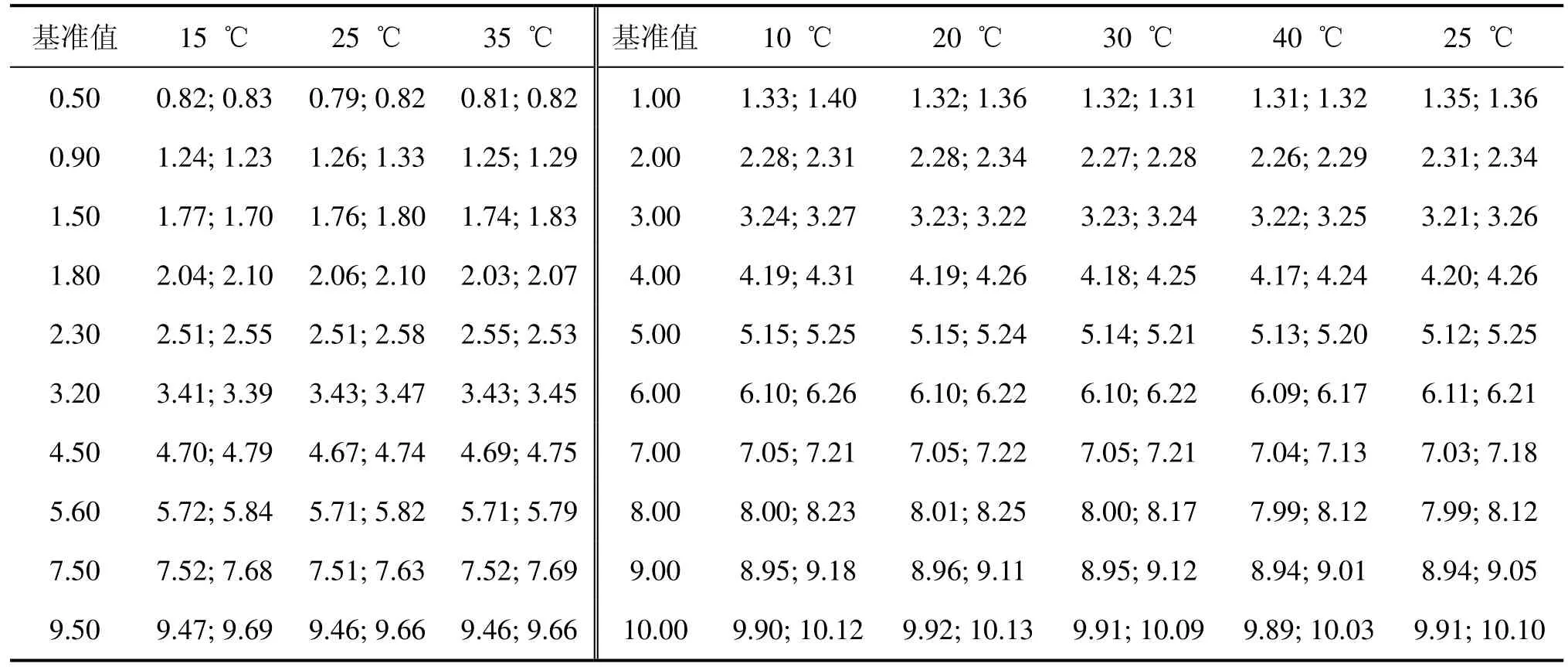
表1 恒流充電過程中典型樣本的電流Table 1 Current of typical sample during constant-current charging process 電流/A

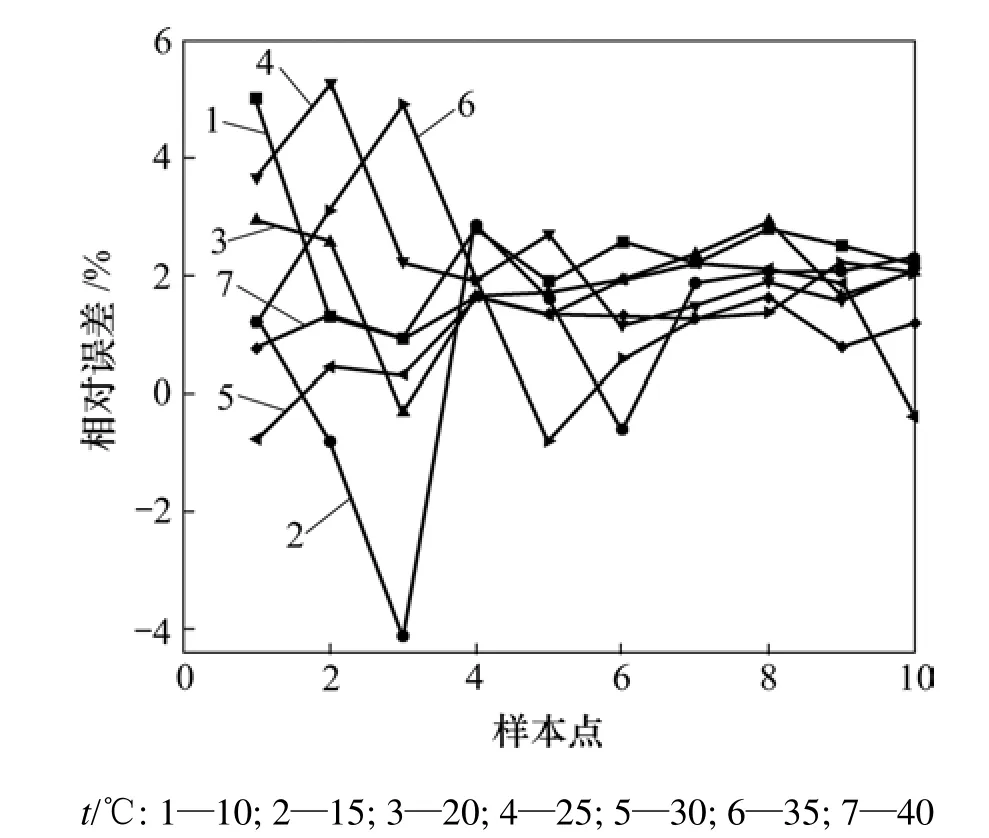
圖2 電流相對誤差Fig.2 Relative errors of electric current

2.3 樣本的預處理

訓練之前，為了保證訓練的準確性，消除其他因素的影響，需對數據進行歸一化。歸一化公式為：

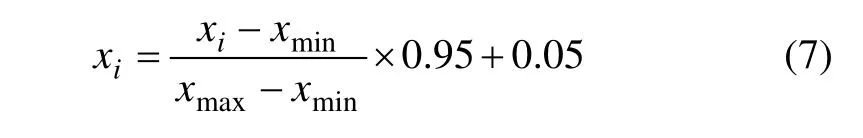
其中：xmax和 xmin分別為每個輸入向量的最大值和最小值。

加入修正數值0.95和0.05的目的是使樣本電流落在[0.05, 0.95]這個區間，避免數據中出現0和1，使網絡具有較好的性能。

3 結果分析

3.1 BP網絡訓練及模型參數優化

用不同隱含層節點數及算法對積累的典型樣本進行訓練，并將訓練好的神經網絡對電路中的電流測量值進行預測，并與實際電流進行比對，得到電流最大相對誤差及平均相對誤差，結果如表2所示。表2中電流均為每項實驗過程中偏差的最大電流。

從表2可知：當采用動量梯度下降法時，網絡不能收斂到設定誤差精度的隱含層節點數分別為 3，4和11；當節點數不為3，4和11時，都可以收斂到設定誤差精度，但是訓練步數全部在1萬步以上，在此優化算法下，隱含層節點的個數為6時效果最好，最大誤差為 2.53%，平均誤差為 0.92%，訓練步數為106 822；而采用L-M算法，網絡不能收斂于設定誤差精度的隱含層節點數都不大于 5，當節點數大于 5時，都可以很快收斂到設定誤差精度，并且訓練步數全部在400以下，當隱含層節點數為9時，最大誤差為0.90%，平均誤差為0.33%，訓練步數為18。通過上述對比可知，采用隱含層節點數為9的L-M算法，其訓練的收斂速度比采用動量梯度下降法要快很多，并且校正的精度比采用動量梯度下降法的收斂速度校正的精度高。

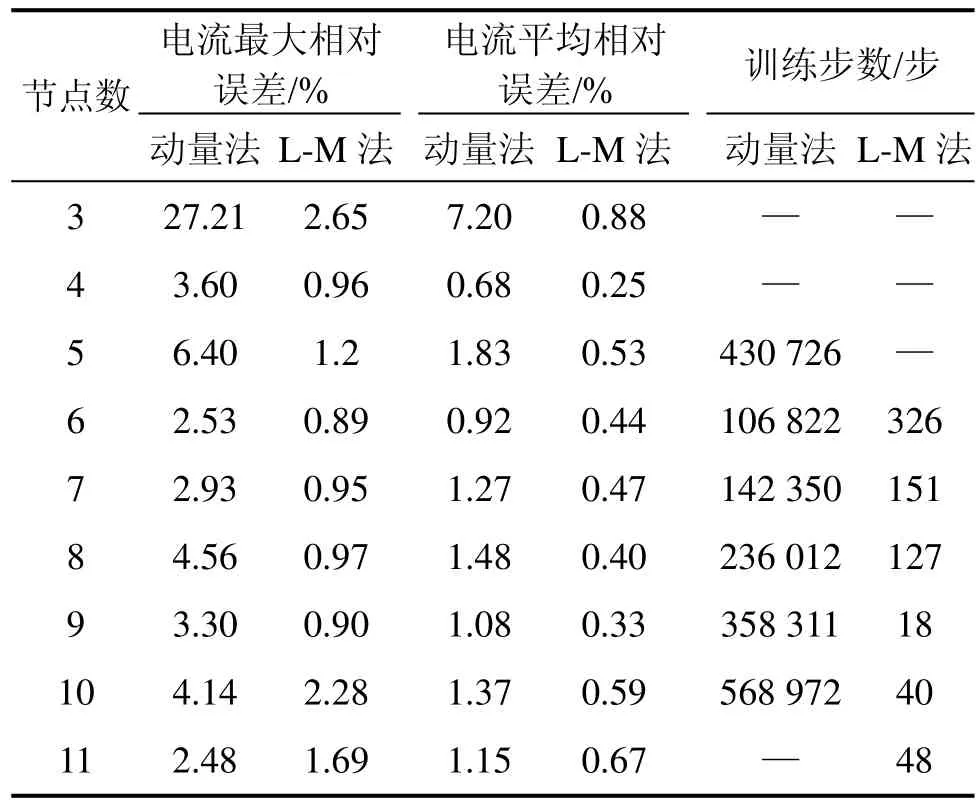
表2 電流的預測結果Table 2 Prediction results of electric current

3.2 設定基準值對應的相對誤差校正結果

采用上述恒流充電過程中得到的L-M BP神經網絡，對采樣電流進行校正，然后，根據校正后的A/D轉換值，通過TL494芯片調節系統回路中的電流，使之接近電流的設定基準。測得基準電流和實測值之間的相對誤差曲線如圖3所示。

圖3 基準電流和實測值之間的相對誤差Fig.3 Relative errors between measured currents and basic set-point currents

由圖3可知：在恒流充電過程中，校正前基準電流和實測值之間的相對誤差隨著電流的增大而減小，校正后基準電流和實測值之間的相對誤差波動較為平緩；基準電流和實測值之間的最大相對誤差由校正前的24%左右下降為校正后的3.5%左右；平均相對誤差由校正前的 6.4%左右減小到校正后的 1.2%左右。可以看出：基準電流和實測值之間的最大相對誤差比校正前明顯下降；平均相對誤差的下降也很顯著。

采用相同的網絡模型，在恒壓充電、恒流放電過程中，得到電流基準值與實測值間的最大相對誤差小于 1.1%，平均誤差為 0.5%左右。表明校正后設定基準和實測值的誤差也得到了較好控制。

4 結論

(1) 隱含層節點數為9的L-M BP神經網絡算法對工業采樣的樣本能較快收斂，并且校正效果明顯比采用動量梯度下降法的BP神經網絡的校正效果好。

(2) 在恒流充電過程中，用L-M BP神經網絡算法能將電流的誤差控制在 0.9%以內；采用通過校正的A/D轉換值調整實際電流，校正后基準和實測值最大誤差在3.5%左右，表明此方法能在一定程度上提高系統精度。

(3) 對于神經網絡算法，訓練樣本的選擇對降低訓練成本和提高網絡泛化能力有較大的影響。訓練樣本除了數量要足夠多外，還應涵蓋各種可能出現的樣本類型，以滿足各種樣本組合和擬合精度要求。本文沒有考慮樣本的選擇對網絡泛化能力的影響，同時也沒有考慮設備的老化等可能導致影響精度的問題，所以，神經網絡算法能否真正可靠地應用在對穩定性要求很高的工業生產設備上還有待進一步驗證。

[1]ZENG Yu-qun, WU Kai, WANG De-yu, et al. Overcharge investigation of lithium ion polymer batteries[J]. Journal of Power Sources, 2006, 160(2): 1302?1307.

[2]龐靜, 盧世剛, 劉莎. 鋰離子電池過充特性的研究[J]. 電化學,2005, 11(4): 398?401.PANG Jing, LU Shi-gang, LIU Sha. A study of overcharge characteristic of lithium-ion cells[J]. Electrochemistry, 2005,11(4): 398?401.

[3]周震濤，覃迎峰. 鋰離子電池過充電行為研究[J]. 電池, 2004,34(5): 326?327.ZHOU Zhen-tao, QIN Ying-feng. A study of the overcharge behavior of Li-ion batteries[J]. Battery, 2004, 34(5): 326?327.

[4]王震坡, 孫逢春, 林程. 不一致性對動力電池組使用壽命影響的分析[J]. 北京理工大學報, 2006, 26(7): 578?580.WANG Zhen-po, SUN Feng-chun, LIN Chen. An analysis on the influence of inconsistencies upon the service life of power battery packs[J]. Transactions of Beijing Institute of Technology,2006, 26(7): 578?580

[5]陳松林, 李革臣, 武云麗. BP神經網絡在電池分選中的應用[J]. 哈爾濱理工大學學報, 2001,6(5): 10?13.CHEN Song-lin, LI Ge-chen, WU Yun-li. The application of BP neural network in battery-sorting[J]. Journal of Harbin University of Science and Technology, 2001, 6(5): 10?13.

[6]凌國維, 唐致遠, 王琪. 人工神經網絡在鋰離子動力電池管理中的應用[J]. 電源技術, 2006, 130(10): 849?851.LING Guo-wei, TANG Zhi-yuan, WANG Qi. Utilization of artificial neural networks in Li-ion power batteries management[J]. Chinese Journal of Power Source, 2006, 130(10):849?851.

[7]周繼成, 周青山, 韓飄揚. 人工神經網絡[M]. 北京: 科學普及出版社, 1992: 47?56.ZHOU Jin-cheng, ZHOU Qing-shan, HAN Piao-yang. Artificial neural network[M]. Beijing: Popular Science Press, 1992:47?56.

[8]史春朝. BP神經網絡算法的改進及其在PID控制中的應用研究[D]. 天津: 天津大學電氣與自動化工程學院, 2006: 41?54.SHI Chun-zhao. Study on algorithm improvement of BP neural networks and its application in PID control[D]. Tianjin: School of Electrical and Automation Engineering, Tianjin University,2006: 41?54.

[9]An G. The effect of adding noise during back-propagation training on a generalization performance[J]. Neural Computation,1996, 8(3): 643?671.

[10]何發祥, 黃英. 用BP網絡求解土體的導熱系數[J]. 巖土力學,2000, 21(1): 84?87.HE Fa-xiang, HUANG Ying. Solution of thermal conduction coefficient from BP network[J]. Rock and Soil Mechanics, 2000,21(1): 84?87.