基于MUSIC算法的多普勒引信目標定位

李 濤,李國林,廖輝榮

(海軍航空工程學院,山東煙臺 264001)

0 引言

近炸引信技術的發展方向之一是擁有精確的空間定位能力。目前引信普遍采用的天線波束定位在提高空間定位能力上已遇到了瓶頸。利用彈目交會過程中多普勒頻率的變化可以實現目標定位。對于無線電引信而言,其工作時間短,且彈目交會過程中多普勒頻率變化,因此實現定位需要估計瞬時多普勒頻率,另一方面由于彈目距離近,目標須以多點散射模型建模[1],因此實際情況是多個變化的頻率同時存在的估計問題,此時常規譜估計方法的分辨率不能滿足要求,為此本文提出在小合成孔徑的基礎上采用M USIC算法估計多普勒頻率實現目標定位。

1 合成孔徑與MUSIC算法原理

合成孔徑是利用天線與目標間的相對運動造成的多普勒頻移現象來工作的,其基本原理如圖1所示。設天線以速度v沿直線運動,M個目標回波信號分別從θi(i=1,2,…,M)方向反射回天線,經過相參混頻后濾波輸出的多普勒回波信號為:

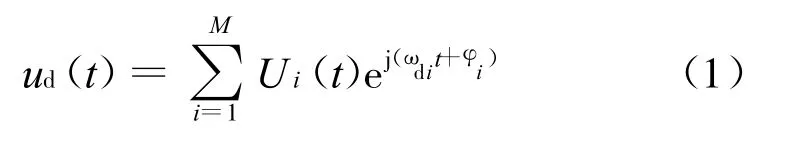
式中,Ui(t)和φi分別為各個回波信號混頻后的幅度和相位,ωdi為多普勒角頻率,且

λ0為載波波長。

圖1 合成孔徑原理Fig.1 Principle of synthetic aperture

根據圖1的方式構建合成陣列,設陣元個數為N,陣列間隔為d,則合成孔徑為L=(N-1)×d,且

式中,Δt為天線陣元運動到下一個陣元位置所經歷的時間,以初始陣元位置為參考,由式(1)、式(3)知第k個陣元的多普勒回波信號可表示為:

式中

為第i個回波信號,nk(t)為第k個陣元的接收噪聲。合成陣列的輸出快拍矢量表示為:

式中

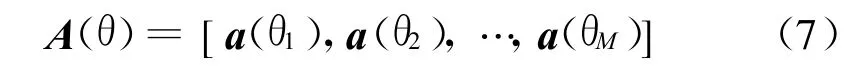
為N×M維陣列流形矩陣,a(θi)為方向向量,且有

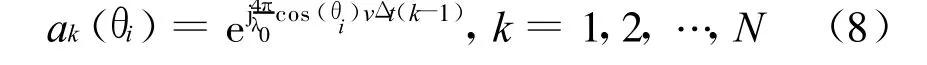
S(t)和N(t)分別為回波多普勒信號矢量和噪聲矢量。設陣列輸出信號自相關陣為:

采用常規譜估計算法(CBF)時,空間譜為:

式中,a(θ)為搜索方向向量。CBF算法的分辨率取決于陣列孔徑大小,使得當陣元數小時難以滿足要求。

MUSIC算法[2]是一種高分辨算法,自出現以來就一直受到關注[3-6],其在小陣元數時依然具有很好的分辨率,算法原理是對R進行特征分解,由R的N-M個小特征值對應的特征向量U張成N-M維噪聲子空間,空間譜為:

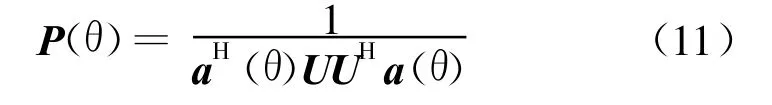
式(11)的搜索峰值結果給出目標方位。

2 基于MUSIC算法的小合成孔徑多普勒引信目標定位

上述合成孔徑假定信號到達角度為常量,不能簡單應用于彈目交會過程。以空對空彈目交會為例,如圖2所示的交會示意圖,天線以相對目標速度v沿直線運動,假設目標存在M個強反射點,M個回波信號分別從θi(i=1,2,…,M)方向反射回天線,由式(2)知,由于彈目相對位置的變化θi將發生改變,因而各個回波信號多普勒頻率將隨時間變化。

圖2 彈目交會示意圖Fig.2 Intersecting of missle and target

由于式(9)的信號自相關陣R需要通過多次快拍矢量的平均來估計,因此在形成多次快拍的批次數據內需要假定頻率變化很小(或者說方位改變量很小),頻率估計要在有限的數據內完成,這可以通過對回波數據進行加窗處理來實現,加窗后形成一個批次的數據,即可采用批次內的數據構建合成陣列輸出快拍矢量來估計R,即

K為用來平均的快拍數據數,為保證能夠構建足夠的快拍矢量來估計R,合成孔徑的陣元數目要足夠小。

注意到圖2的彈目交會過程中,當彈目距離較遠時,目標方位的改變很慢,同時目標的M個回波信號的到達角靠得很近,因此可以采用較大的批次數據,同時構建陣元數稍大的合成孔徑以提高分辨率,當彈目距離逐漸接近時,目標方位改變加快,但回波信號的到達角將分得越來越開,這時可以逐步縮小批次數據和陣元數,因此,加窗的寬度和陣元數目可以隨彈目的接近逐漸減小。

加窗的寬度和合成陣元數確定后,接下來是采用批次數據構建式(12)中的合成陣列快拍矢量X(ti)。對于線性天線陣列而言,理想的陣元間距為半個載波波長。因此當采用合成孔徑時,理想的陣元間距為λd/2,λd為多普勒頻率波長,但不同方向的回波多普勒頻率不一樣,因此為防止欠采樣,需選取最大多普勒頻率的半波長作為式(3)的陣元間距,由于彈目交會過程中的多普勒頻率會逐漸變小,因此最大多普勒頻率可選擇為由前一個批次數據估計的最大多普勒頻率,設為,則陣元間距為:

根據式(2),初始 fm值可以選擇為:

將陣元間隔換算成時域采樣間隔為:

實際的回波信號采樣間隔可能并不符合式(15),一般小于T,設采樣間隔為Td,為保證不出現欠采樣,最佳采樣間隔應該為:

其中

其中運算 ·表示向下取整運算。根據n值快拍矢量的構建方式可以通過圖3來說明。

圖3 數據快拍結構Fig.3 Structure of data snapshoot

如圖3,經過混頻后的回波采樣序列經過n路單位延時后,對每一路進行n倍下抽樣,n由式(16)決定。當陣元數為N時,下抽樣的每一路輸出結果的每N個連續數據即構成一次快拍數據。

設以Nsum個采樣數據為一個批次(即加窗寬度為),則式(12)中K為:

總結基于MUSIC算法的多普勒引信目標定位算法為:

1)根據體目標模型、彈目相對速度v選擇合成陣列陣元個數N、加窗寬度Nsum和初始最大多普勒頻率 fm0,其中N和Nsum值可選擇隨彈目的接近逐漸變小;

2)根據最大多普勒頻率 fm和回波信號的采樣間隔Td根據式(16)選擇n;

3)由n采用圖2的方式構建陣列輸出快拍矢量;

4)由式(12)估計陣列自相關陣,其特征分解得到噪聲子空間矩陣U;

5)根據式(11)搜索空間譜,其峰值給出目標反射點方位估計。

3 算法仿真

仿真設發射信號載頻為7.5 GHz,天線平臺運動速度為200 m/s,彈目中心距離為50 m,脫靶量為10 m,則 fdmax=10 kHz,信號采樣率 fTd=1/Td=1 MHz,Nsum=3 200,N=16,由式(15)知n=50。定義Lmax為考慮每個批次回波數據為Nsum時,其對應可合成的最大孔徑

由圖4知3個方向的回波信號在采用CBF算法估計方向時無法分辨,而MUSIC算法的結果則完全能夠分辨。圖中給出了基于 N=16和考慮到批次數據對應的最大孔徑Lmax,即等效于N=64時的CBF算法估計結果,可見基于MUSIC算法的空間譜估計能夠在合成陣元數N較小時取得較之常規空間譜估計高得多的分辨率。

圖4 基于M USIC算法和常規波束空間譜估計結果(N=16)Fig.4 The result of M USIC and CBF spatial spectrum estimation(N=16)

將陣元數改成N=4,Nsum=1 600,由式(19)知等效最大孔徑等效為32個陣元。其他參數不變,圖5給出了空間譜估計的結果。由圖可見,即使在陣元數N=4的場合,采用MUSIC算法依然能夠取得較好的分辨率。對于N=4的場合來說,MUSIC算法的計算量即使是在無線電引信需要實時計算的場合也是完全能夠做到的。

圖5 基于M USIC算法和常規波束空間譜估計結果(N=4)Fig.5 The result of M USIC and CBF spatial spectrum estimation(N=4)

4 結論

綜上所述,本文提出的基于MUSIC算法的小合成孔徑多普勒引信目標定位方法。該方法先采用合成孔徑技術來構建小陣元數天線陣列,并對回波信號進行加窗處理,由窗內數據估計陣列輸出自相關陣,然后利用MUSIC算法估計目標多反射點回波信號到達角實現目標精確定位,算法實現時通過采用小合成孔徑和對回波數據進行加窗處理來減小多普勒頻率變化的影響,合成陣元數和加窗寬度隨彈目距離的接近逐漸減小。仿真結果表明:算法能夠實現多普勒頻率的高分辨率估計,適合導彈與體目標交會過程中目標多反射點定位,且合成小陣元數滿足實時計算的要求。

[1]李在庭,方再根,何遵文,等.無線電近炸引信空中目標的建模和分析[J].兵工學報,1995(1):28-32.

[2]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE T rans Antennas and Propagation,1986,34(2):276-280.

[3]余繼周,陳定昌.一種DOA估計的快速子空間算法[J].現代電子技術,2005,28(12):91-92.YU Jizhou,CHEN Dingchang.A fast subspace algorithm for DOA estimation[J].M odern Electrollics Technique,2005,28(12):91-92.

[4]周偉,馮大政,劉建強.一種新穎的DOA估計算法[J].電子與信息學報,2005,27(10):1 513-1 516.ZHOU Wei,FENG Dazheng,LIU Jianqiang.A novel approach to DOA estimation[J].Journal of Electronice&Information Technology,2005,27(10):1 513-1 516.

[5]吳云韜,廖桂生,陳建峰.一種色噪聲環境下的DOA估計新算法[J].電子學報,2001,29(12):1 605-1 607.WU Yuntao,LIAO Guisheng,CHEN Jianfeng.A novel method for estimating DOA in the presence of unknown colored noise fields[J].Chinese Journal of Electronice,2001,29(12):1 605-1 607.

[6]Weber R J,HUANG Yikun.Analysis for capon and MUSIC DOA estimation algorithms[C]//Antennas and Propagation Society InternationalSymposium.APSURSI:IEEE,2009:1-4.