數據挖掘技術在公路交通管理系統中的應用研究
秦 佳
數據挖掘技術在公路交通管理系統中的應用研究
秦 佳
介紹了用于預測決策的回歸分析方法,進行預測決策數據挖掘模型設計,并用公路交通管理系統中違章數據進行驗證,得出較優的用于公路交通管理預測決策的數據挖掘模型。
數據挖掘;預測決策;回歸分析
數據挖掘作為數據倉庫技術的重要應用,利用一系列方法,從海量數據中提取隱含在其中的有用信息和知識,并對數據進行深層分析、挖掘,為企業提供綜合性分析決策信息。實現數據共享,統一分析平臺的數據環境,為高質量的決策提供堅實的數據基礎。
公路交通管理系統是在原闖紅燈抓拍系統的基礎上,對抓拍的圖片進行后臺管理的系統,擴展了對于監測不按導向車道行駛、停車壓線、超速等各種違法行為的綜合管理。利用數據挖掘技術,對交通違規車輛數據進行分析和處理,初步實現交通違規車輛管理的分析和管理預測功能。
利用回歸分析的方法,進行數據挖掘,建立包括時間變量在內的線性回歸模型。預測時,輸入任意的時間和自變量,利用回歸模型對目標進行預測。
1 模型的影響因素
影響交通管理的因素很多,主要體現在闖紅燈、酒后駕車、無證駕駛、超載、上下班高峰時間、主要地段車流量、路況、天氣等方面。為了優化模型,便于數據的處理,使之更加貼近實際情況。
采用多元線性回歸的方法建立公路交通管理預測模型,利用四元線性回歸方程,分析影響因素與公路交通管理預測之間的線性關系,從而簡化分析過程,提高系統預測和決策能力。現將闖紅燈(rtrl_id)、酒后駕車(drunk driving_id)、上下班高峰時間(time_id)、天氣(climate_id)這四個影響因素作為自變量,利用回歸輸出的連續變量,用于公路交通管理的預測。
2 模型的數據處理
為了保證數據的一致性、有效性和層次性,要有統一數據的來源,為數據挖掘做準備。采用某市交通綜合信息數據倉庫,作為公路交通管理預測模型的數據來源。利用OLAP技術,將不同的多個點的 POS 系統數據及不同類型的數據,從數據庫系統中抽取、轉換并加載到數據倉庫。在建立好的數據倉庫中,將系統網絡中記錄著來自不同地段的交通基本數據(交通的基本信息和車輛的違章細節)集中在一起,作為源數據,其數據類型可為Access、Oracle、SQL Server 及文本文件等。
針對不同的預測影響因子,對數據進行最細粒度的匯總和加工,形成面向多個層面的新的、詳細的數據和層匯總數據,在保證系統運行穩定的前提下,使得預測的主題完善、豐富。而在數據倉庫中,存儲的是以季度或月為粒度的當前基本數據和歷史基本數據,就要對其按日為粒度作為預測數據的基礎,再用于數據挖掘。
數據預處理的方法:在事實表中的rtrl_id、drunk driving_id、time_id、climate_id,利用 SQL Server 2000 中建立的 DTS 包,將時間維表與之相關聯,進行轉換處理,提取出所需的時間單位用于預測模型的計算。
3 模型的建立及檢驗
3.1多元線性回歸模型。
設研究對象受多個因素x1,x2,x3…,xm(自變量)影響,各影響因素與預測目標y(因變量)的關系是線性的,則其多元回歸線性模型為:
yi=β0+β1xi1+β2βi2+…+βmxim+εi(i=1,2,…,n)
(1)
式中:
yi,xim——預測目標和影響因素的第i組觀測值;
εi——第i組觀測值對yi的隨機誤差;
β0,β1,…,βm——m+1個待估計的回歸參數。
在多元線性回歸模型中,做如下假設:①y與xj(j=1,2,…,m)之間滿足線性關系;②xj是確定性變量,且在兩個自變量或多個自變量之間存在線性關系;③隨機誤差ε服從正態分布,且ε~N(0,σ2)。
其矩陣形式為:
Y=XB+ε
(2)
式中:
(3)
3.2模型檢驗。
為了判斷多元線性回歸模型所反映的各變量之間的關系形式是否符合客觀實際,引入的因素是否有效,在將模型用于實際預測前,需對模型進行檢驗。常用的檢驗方法有R檢驗、F檢驗和t檢驗。
1)R檢驗:R稱為復相關系數或全相關系數,R的計算公式為:

(4)
R說明x1~xm這一組影響因素與y的相關程度。利用R進行判別時,根據回歸模型的自由度n-m和給定的顯著性水平α,從相關系數臨界值表中查出臨界值Rα(n-m),若R≥Rα(n-m),表明模型的自變量和因變量間線性相關關系顯著,檢驗通過,模型可用于預測;若R 2)檢驗:用來檢驗整個回歸系數是否有意義,F的計算公式是: (5) 式中:m——影響因素的個數; n——統計資料的個數。 F服從第一自由度為m-1,第二自由度為n-m的F分布,給定顯著水平α,查F分布表得Fα(m-1,n-m),如果F>Fα(m-1,n-m),則認為這一組回歸系數有意義,可以利用所建立的多元線性回歸預測模型進行預測;否則認為這一組回歸系數無意義,所建立的多元回歸模型不成立。 3)t檢驗:R檢驗和F檢驗都是將所有的自變量作為一個整體,來檢驗它們與因變量y的相關程度以及回歸效果,而t檢驗則是用來對每個回歸系數是否有意義進行的檢驗。 (6) Cjj—矩陣(X' X)-1主對角線上的第j個元素。 若|tj|>tα/2(n-m),說明xj對y有顯著影響,可用于預測,反之,說明xj對y無顯著影響,應刪除該影響因素,調整回歸模型。 為了驗證四元線性回歸公路交通管理預測模型的可行性,選取某市2008—2009年兩年的數據,按月匯總后的公路管理信息。將2008年數據用于建模,2009年數據作為模擬數據,分6組用于評估預測的正確率。利用Matlab7.0編程分析實現公路管理預測模型的數據挖掘,分別用 R 檢驗、F 檢驗和 t 檢驗法進行模型評估,結果表明模型合格。并采用平均絕對百分比誤差 MAPE 來評估預測的精確性,預測結果見表1。 (7) 式中:yi——第i期實際值; fi——第i期預測值。 表1 預測結果 一個評價預測精度的參考標準認為,平均絕對百分比誤差在 20%~50%之間的為可行預測,高于50%的為良好預測。通過對線性回歸預測模型的驗證,總的平均百分比誤差為42.86%,說明此模型用來進行公路交通管理預測是可行的。但還存在以下不足: (1)回歸分析方法只是用靜止的觀點描述各變量之間的因果關系,而沒有考慮現實交通活動的動態發展。 (2)交通的需求往往是由許多因素綜合決定的,但不可能對所有因素進行建模,而只能考慮其中的一部分,這就已經存在著誤差。 [1]徐國祥. 統計預測與決策[M]. 上海財經大學出版社,2001. [2]包翠蓮,開小明. MATLAB 語言在多元線性回歸中的應用[J]. 安徽教育學院學報,2005, (3):23. [3]李海宏. 基于企業數據倉庫系統的數據挖掘工具的實現[D]. 四川大學,2003. [4]王艷輝,王卓,賈利民等. 鐵路客運量數據挖掘預測方法及應用研究[J]. 鐵道學報,2004, (5):26 . OnApplicationofDataMiningTechnologyinHighwayTrafficManagementSystem Qin Jia The paper introduced the regression analysis method used in the expectation and decision-making. The model the data being used in decision-making is designed. The testing and checking of the rules and regulations has been made and the data mining model applied to the highway traffic management system has been found out . data mining;forecast and decision;regression analysis ClassNo.:TP311.131DocumentMark:A 孔祥春 鄭英玲) 秦佳,碩士,講師,雞西大學電氣與信息工程系,黑龍江·雞西。郵政編碼:158100 1672-6758(2010)06-0040-2 TP311.131 A

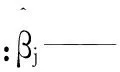
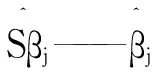

4 模型的評估與分析


