企業知識產權交易定價的博弈分析

劉衛國，李乾文

（南京審計學院 管理學院，南京 211815）

企業知識產權交易定價的博弈分析

劉衛國，李乾文

（南京審計學院 管理學院，南京 211815）

知識產權定價過程是買賣雙方討價還價的博弈過程，文章以博弈理論為基礎，嘗試構建了知識產權交易博弈模型并進行了簡單分析，指出在知識產權交易非重復博弈中，買賣雙方存在五種可能的博弈結果，最后給出知識產權質量高或質量低時，賣方選擇定高價或定低價出售的判斷標準。

知識產權；信號博弈；定價；博弈分析

現實生活中，買賣雙方在進行知識產權交易時，價值只是交易的一張底牌，最后成交價格的確定則是買賣雙方討價還價(博弈)的結果。事實上作為一種市場經濟行為，知識產權交易實質上是買賣雙方在追求各自利益最大化前提下所進行的信號博弈行為。因此用博弈論的思想方法去分析知識產權交易定價就顯得非常必要，這對于提高知識產權交易的理性，引導并規范知識產權交易市場健康、穩定發展具有深遠的意義。

1 知識產權價值確定的傳統方法

國內外經濟學論著中介紹的知識產權價值確定方法有很多，但是這些方法在邏輯上大體可以分為三種基本類型，通常稱為收益現值法、成本法和市場法。

1.1 收益現值法

收益現值法是將知識產權在使用年限內帶來的未來凈收益按照一定折現率折現的總價值作為知識產權價值。其基本計算公式如下：

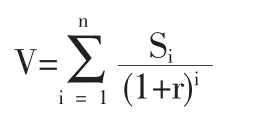
式中：V表示為知識產權評估價值；Si表示第i年的知識產權收益預測值；n表示知識產權的壽命期；r表示折現率。

收益現值法是把被評估知識產權剩余壽命期間內的預期未來收益，按照一定的貼現率，折成現值，來確定被評估知識產權價格的方法。因此，它只適用于直接產生收益的經營性資產，該類資產通過生產經營帶來收益，同時通過生產經營的進行，其在若干個會計期間內會連續不斷地創造出收益。知識產權屬于生產要素或稱經營性資產，其價值是通過對知識成果的利用而產生或預期產生的收益，因此，對知識產權價值評估最為適當的方法應為收益現值法。國外學者Reilly和 Dandekar曾對包括知識產權在內的各類無形資產評估的適用方法作過較詳細的分類，其研究成果顯示，已批準的專利、商標與商譽、版權(計算機軟件除外)的評估主要都是采用收益現值法[1]。

1.2 市場價值法

市場價值法是通過市場調查，選擇一個或幾個與評估對象相同或類似的資產作為比較對象，針對各項價值影響因素，分析比較對象的成交價格和交易條件，將被評估資產與比較對象逐個進行對比調整，估算資產價值的方法。市場價值法只有存在與被評估資產相類似的資產交易市場時才適用。由于知識成果具有新穎性、創造性，一般不會出現完全相同的知識成果。另外，我國企業從20世紀90年代才開始逐漸重視知識產權，知識產權的交易也就經歷了不到20年的時間，不僅交易的歷史短，交易的數量也不多，說明了可使用的知識產權交易的歷史資料是有限的。因此，在運用市價價值法對知識產權進行評估時，由于對某些知識產權獲取市場信息的局限性，評估人員很難找到比較合適的歷史可比資料，轉而求其次。這樣難免會造成評估結果的失真。但是在條件適當的情況下，采用市場法確定知識產權的價值也是一種較可行的方法。

1.3 重置成本法

重置成本法是以重新建造或購置與被評估資產具有相同用途和功效的資產現時需要的成本作為計價標準。其基本原理是按重置成本價格對知識產權進行估價，即按照評估知識產權全新狀態的重置成本減去該項產權功能性貶值和經濟性貶值估算知識產權價值的方法。由于知識產權價值的特殊性，應用成本法評估其價值存在很大障礙。例如，對技術商品而言，其生產過程是高度復雜的腦力勞動過程，具有探索性和創造性，不像一般商品的生產可以進行模式化勞動；對專利而言，由于專利只授予首先申請發明的人，如果被人捷足先登，即使耗費很大也是前功盡棄。或即便取得專利，很快又有人開發出更先進的取代技術，也收不到預期效益；對于商標而言，要想找到商標的重置成本是困難的。由于這些問題的存在，在使用重置成本法確定知識產權的重置成本時，很難保證評估結果不失真。因此，一般情況下，重置成本法不宜作為評估知識產權的方法。

總的來講，采用收益現值法、市場價值法和重置成本法確定知識產權價格的方法要么是從買賣雙方其中某一方角度考慮問題，要么是從市場的角度考慮問題，都不是非常全面，筆者認為知識產權交易價格應該通過買賣雙方討價還價的過程確定。

2 知識產權交易定價博弈模型構建

在知識產權交易活動中，買賣雙方的交易行為顯然是一種博弈行為：一方面，由于買賣雙方信息不對稱的存在，該博弈是不完全信息博弈；另一方面，整個交易過程經過報價、成交實施或追究違約責任等過程，該博弈還可以看成是動態博弈。

2.1 基本假設

博弈中的主要參與人是知識產權交易雙方。為了簡便分析，本文僅使用交易雙方作為參與人構建博弈模型，并做出如下假設：

⑴假設知識產權交易成功與否只取決于參與博弈的買賣雙方，知識產權制度、知識產權市場狀況、知識產權關系等作為外部因素暫不考慮。

⑵假設參與人都是理性的，嚴格追求自身利益最大化，因而具有進行交易獲取潛在收益的動力。

⑶假設知識產權有質量高、低兩種情況，買方估計這兩種情況能產生的未來現金流的現值分別Vg和Vb，且Vg＞Vb。同時，賣方知識產權的質量信息屬于私人信息，買方只知道賣方的定價，只能根據賣方的定價來判斷知識產權的質量，即對賣方知識產權的質量具有不完全信息。

⑷假設買方的全部可選策略包括買或不買，賣方的全部可選策略包括定高價或定低價，分別用Ph和PI表示，且Ph＞Pl。賣方在知識產權質量高時可以選擇高定價或低定價，而且在知識產權質量低時同樣也可以選擇高定價或低定價。賣方對質量高、低的知識產權付出的努力成本分別為Ch和CI；C1為賣方對質量低的知識產權選擇定高價時所花費的包裝成本；C2為質量低的知識產權定高價被買方識破后，市場對賣方所追加的懲罰成本。

⑸而且 Vg＞Ph,Vb＞Pl，Vl＜Ph，否則，產權交易行為不會產生（假定交易雙方的賣價、買價等都是在充分考慮了各種可能影響因素的基礎上理性做出的)。

⑹買方不能討價還價，要么接受賣方定價，要么不買。

⑺使用凈收益指標來衡量博弈雙方的得益。如果交易成功，當知識產權質量高時，若賣方選擇定高價，買方和賣方的得益分別為Vg-Ph、Ph-Ch，若賣方選擇定低價，買方和賣方的得益分別為Vg-Pl、Pl-Ch；當知識產權質量低時，若賣方選擇定高價，買方和賣方的得益分別為Vb-Ph、Ph-Cl-C1，若賣方選擇定低價，買方和賣方的得益分別為Vb-Pl、Pl-Cl。如果交易失敗，若賣方的知識產權質量低，定高價將有損失C=-Cl-C1-C2，定低價將有損失-Cl，若賣方的知識產權質量高，定高價和低價都損失-Ch，賣方不購買的得益均為0。

⑻為簡化分析，假設 Vg-Ph＞Vb-Pl＞0＞Vb-Ph，即用高價購買質量高的知識產權比用低價購買質量低的知識產權收益大；而低價購買一個質量低的知識產權還不至于取得負的收益。如果買方用高價購買質量低的知識產權就可能會取得負的收益；買方用低價購買質量高的知識產權的收益是最高的，這時可能存在知識產權價值被市場低估或存在某些關聯交易、利益輸送的可能性[2]。

根據上述假設，買方購買知識產權的期望收益為：

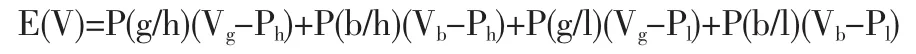
公式中的四個概率依次為定價高的知識產權質量高、定價高的知識產權質量低、定價低的知識產權質量高、定價低的知識產權質量低的條件概率。顯然，當E(V)≥0時，買方選擇購買；當E(V)＜0時，買方放棄購買。

2.2 知識產權交易的博弈過程分析

考慮到交易雙方信息的不對稱和雙方交替決策的動態過程，可以這樣思考該博弈問題：

第一階段，自然n選擇知識產權的類型，為了簡便起見，我們假設賣方知識產權的類型只有質量高、低兩種情況，賣方知識產權類型集以θ={g,b}表示，其中g代表賣方知識產權質量高，b代表賣方知識產權質量低，假設知識產權質量高的先驗概率用p(g)表示，知識產權質量低的先驗概率用p(b)表示，且滿足:p(g)+p(b)=1，其中：

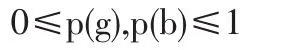
第二階段，賣方根據自然n的選擇，選擇定價p作為信號，信號空間為 P={Ph,Pl}，其中 Ph為定高價，Pl為低定價，Ph＞Pl。

第三階段，買方不知道知識產權的類型θ，只知道知識產權屬于θ的概率分布p(θ)，當賣方向買方發出信號p時，買方根據賣方發出的信號（定價P），應用貝葉斯法則修正先驗概率，并得到關于知識產權質量高或低的后驗概率p(θ/P)，然后根據p(θ/P)從行動集以A={a1,a2}選擇一個行動，決定買或不買，其中a1表示買，a2表示不買。

上述博弈過程用博弈樹表示就是如下的擴展式：

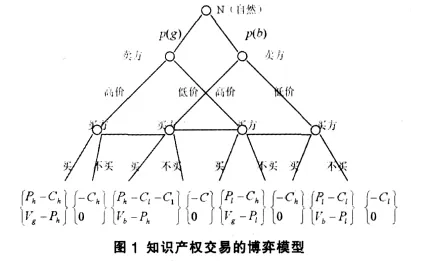
圖1終點括號內的上面的數字為賣方的得益，下面數字為買方的得益。一般情況下，由于賣方在知識產權質量高、低兩種情況下都有選擇定高價和低價的可能性，因此買方不能根據賣方出價的高低而簡單地判斷知識產權的質量，他還要進行其他信息的搜集與分析。因此買方必須根據賣方的定價和自己過去的經驗，參考同類型知識產權的交易價格并且利用貝葉斯法則正確判斷賣方知識產權的質量高低。

不難看出，信號傳遞博弈實際上是不完全信息情況下的斯坦克爾伯格（Stackelberg）博弈（信號發送者是領頭者（Leader），信號接受者是尾隨者（Follewer））[3]。 當參與人 1（賣方）發出信號即價格時，他預測到參與人2（買方）將根據其發出的信號修正對自己類型的判斷，因而選擇一個最優的類型依存信號戰略；同樣，參與人2（買方）知道參與人1（賣方）選擇的是給定類型和考慮信息效應情況下的最優戰略，因此使用貝葉斯法則修正對參與人1（賣方）類型的判斷，選擇自己的最優行動，即買或不買。

3 知識產權交易定價博弈模型的分析與求解

3.1 對參與人2（買方）的分析

3.1.1 定高價時的分析

在賣方出高價時，買方有買或不買兩種選擇，但其最終的選擇則必然是得益中最大者。根據前述分析，于是有：

買方選擇=Max{(P(g/h)(Vg-Ph)+P(b/h)(Vb-Ph))，0}

下面分兩種情況進行討論分析：

①如果買方選擇買，則必有：

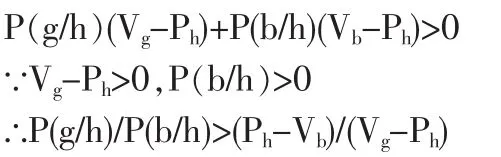
②如果買方選擇不買，則必有：

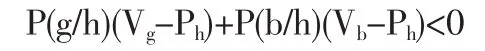
同理，解得：

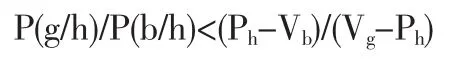
通過上述綜合分析可以得到如下結論：在知識產權交易博弈中，如果賣方定高價，買方選擇買的條件是(g/h)/P(b/h)＞(Ph-Vb)/(Vg-Ph)，選擇不買的條件是 P(g/h)/P(b/h)＜(Ph-Vb)/(Vg-Ph)

3.1.2 定低價時的分析

在賣方出低價時，買方有買或不買兩種選擇，但其最終的選擇則必然是得益中最大者。根據前述分析，于是有：

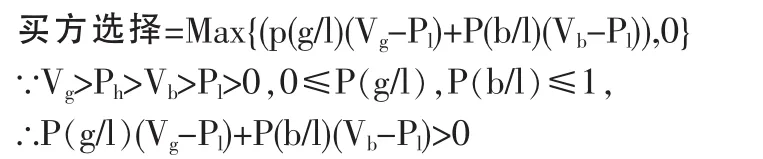
因此，在賣方定低價的情況下，買方的選擇都是買。

3.2 對參與人1（賣方）的分析

3.2.1 相關概率假設

筆者為分析方便，假設：

賣方定高價，買方買的概率：

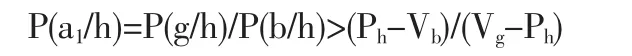
賣方定高價，買方不買的概率：

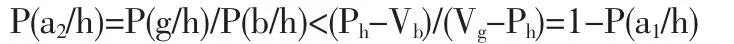
賣方定低價，買方買的概率：P(a1/l)=1

賣方定低價，買方不買的概率：P(a2/l)=1-P(a1/l)=0

3.2.2 知識產權質量高時的分析

在知識產權質量高時，賣方有定低價或定高價兩種選擇，但其最終的選擇則必然是賣方得益中最大者。根據前述分析,可以得知：

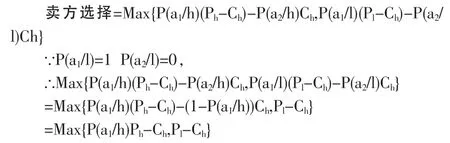
因此，當 P(a1/h)Ph-Ch＞PI-Ch，即 P(a1/h)＞Pl/Ph時，即賣方在知識產權質量高時定高價；當 P(a1/h)Ph-Ch＜Pl-Ch，即 P(a1/h)＜Pl/Ph時，賣方在知識產權質量高時定低價。

3.2.3 知識產權質量低時的分析

在知識產權質量高時，賣方有定低價或定高價兩種選擇，但其最終的選擇則必然是得益中最大者。根據前述分析,于是有：

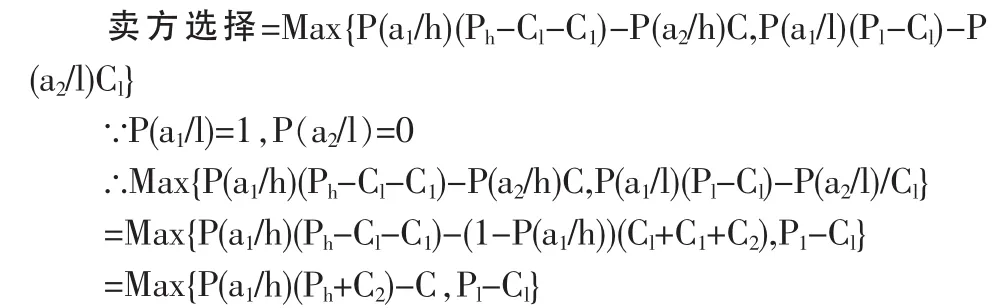
因此，當 P(a1/h)Ph-Ch＞Pl-Ch，即 P(a1/h)＞Pl/Ph時，即賣方在知識產權質量低時定高價；當 P(a1/h)Ph-Ch＜Pl-Ch，即 P(a1/h)＜(Pl+C1+C2)/(Ph+C2)時，賣方在知識產權質量低時定低價。

3.3 知識產權交易定價博弈模型求解

3.3.1 買方博弈模型求解

在賣方定高價時，買方以 P(a1/h)=P(g/h)/P(b/h)＞(Ph-Vb)/(Vg-Ph)的概率選擇購買，以 P(a2/h)=P(g/h)/P(b/h)＜(Ph-Vb)/(Vg-Ph)的概率選擇不買；在賣方定低價時，賣方選擇購買。

3.3.2 賣方博弈模型求解

當買方確定購買時，如果知識產權質量高，買方高價購買的概率P(a1/h)＞Pl/Ph時，賣方定高價，在買方高價購買的概率P(a1/h)＜Pl/Ph時，賣方定低價（特殊情況）；當知識產權質量低時，買方出高價購買的概率P(a1/h)＞(Pl+C1+C2)/(Ph+C2)時，賣方定高價，買方出高價購買的概率P(a1/h)＜(Pl+C1+C2)/(Ph+C2)時，買方定低價。

3.3.3 重復交易博弈分析

從上述分析可以看出，當交易只進行一次時，無論知識產權質量高低，賣方都存在定高價或低價的可能。但是在現實的知識產權交易市場中，買賣雙方的博弈是重復進行的。因此，當某個買方以高價購買了質量較低的知識產權，就會向交易市場反饋賣方定高價的知識產權可能質量低的信息,從而使得后續交易者不斷降低自己高價購買P(a1/h)，最終迫使賣方無法滿足P(a1/h)＞(Pl+C1+C2)/(Ph+C2)的條件，從而減少高價銷售質量較低知識產權的行為。而在知識產權質量高時，由于信息不對稱現象的存在，會存在“劣幣驅逐良幣”的現象(即質量高的知識產權在定高價時也賣不出去)，只能降價出售。如此以往，整個社會的知識產權交易就會步入良性循環的軌道。

4 結論

通過對知識產權交易定價進行了博弈分析，指出獨立的一次性知識產權交易博弈中，買賣雙方存在五種可能的博弈結果，即（質量高，定高價，購買）、（質量高，定低價，購買）、（質量高，定高價，不購買）、（質量低，定高價，購買）、（質量低，定低價，購買）。在知識產權質量高時，賣方選擇定高價或定低價的標準是買方高價購買的概率P（a1/h）是否大于Pl/Ph；在知識產權質量低時，賣方選擇定高價或定低價的標準是買方高價購買的概率P(a1/h)是否大于(P1+C1+C2)/(Ph+C2)；在重復交易的知識產權市場中 （市場有效），買賣雙方只存在兩種博弈結果，即（質量高，定高價，購買）、質量低，定低價，購買）。本文的研究結論對于不斷加強和完善知識產權交易市場建設，促進知識產權交易良性循環和合理配置具有重要的理論指導意義。

[1]Reilly,R.F.,M.P.Dandekar.Valuation of Intangible Contract Rights[J].The CPA Journal,1997，6.

[2]吳漢東.中國知識產權的國際戰略選擇與國內戰略安排[J].今日中國論壇，2006(Z1).

[3]肖軍，劉倩.知識產權的價值向度與制度構建[J].求索，2009，（8）.

[4]張維迎.博弈論與信息經濟學[M].上海:上海三聯書店,上海人民出版社,2004.

[5]王月欣.關于知識產權的定價信號博弈問題[J].理論探索，2008,（4）.

[6]陳悅，倪浩，陶柏.企業并購中的討價還價博弈模型[J].統計與決策，2004，（3）.

[7]王義秋，王琳.企業并購定價的博弈分析[J].東北大學學報(自然科學版),2004,(6).

F224

A

1002-6487(2010)22-0060-03

國家自然科學基金資助項目（70972145）

劉衛國（1974-），男，陜西西安人，博士，講師，研究方向：技術創新管理。

李乾文（1970-），男，河北石家莊人，博士，教授，研究方向：創業管理。

（責任編輯/亦 民）