農產品生產異常波動的預測與實證研究
羅光強,譚江林
(湖南農業大學 經濟學院,長沙 410128)
農產品生產異常波動的預測與實證研究
羅光強,譚江林
(湖南農業大學 經濟學院,長沙 410128)
經濟市場化與供給多元化條件下農產品生產頻繁波動是一個不可避免的特征事實。客觀面對農產品生產的正常波動,努力防止和規避農產品生產的異常波動是一個值得研究的課題。文章首先給出了一個農產品生產異常波動的預測方法與模型,然后以湖南糧食生產為例進行了相關實證分析。
農產品生產;異常波動;預測方法
0 引言
2010年中央一號文件精神指出,要完善農產品市場調控機制,保持農產品市場穩定。這是針對當前國內外經濟增長明顯放緩和農產品生產波動的新形勢,實施的一項保障農產品穩定增長的重大任務。因此,努力減少農產品生產波動,積極促進農產品生產穩定增長是一個值得研究的重大課題。既有的相關研究主要集中于各類農產品生產波動規律和趨勢的分析,其目的是試圖通過提供預期市場信號,發揮市場機制的調控功能,促進農產品生產的穩定增長。但是,由于農產品生產具有典型的弱質性特征,農產品生產存在的蛛網現象僅僅依靠市場功能是難以解決的,徹底消除或完全規避農產品生產的波動問題是不現實的。基于此,本文試圖引進農產品生產異常波動的概念,并以湖南糧食生產為例展開農產品生產異常波動的預測研究,以便在客觀面對農產品生產正常波動的規律條件下為防止和規避農產品生產異常波動的政府干預行為提供決策參考。
1 農產品生產異常波動的預測方法
1.1 研究方法
目前常用于預測趨勢的模型大致包括以下幾種:(1)回歸關系類模型。這類模型的特點是被預測事物與其影響因素之間,在一定時間內保持著某種固定結構函數關系,可以通過一元或多元回歸的方式來表述。(2)因果關系類模型,這類模型的特點是在被預測事物與其影響因素之間的關系是用因果形式描述的,Granger對此進行了深入研究,提出了Granger因果關系的計量經濟模型。(3)投入產出測算法。該方法的主要觀點是根據影響糧食生產的各種要素的投入狀況來測算糧食的期望產量。(4)灰色模型。是以灰色生成函數概念為基礎,以微分擬合為核心的建模方法,將雜亂無章的原始數據序列通過一定的處理方法弱化波動性,使之變為比較有規律的時間序列數據,再建立用微分方程描述的模型,該方法本質來講也是一種時間序列模型。(5)時間序列模型。這種方法主要是通過建立預測對象與綜合指數之間的時間序列相關辨識模型。該模型在預測方面的應用如今發展較快,博克斯—詹金斯方法是該領域發展比較成熟的模型,用回歸移動平均模型(ARMA)、齊次非平穩模型(ARIMA)等來預測未來變化。本文將采用博克斯—詹金斯方法,以歷年湖南糧食總產量為依據,通過其趨勢圖形擬合出與之相似的指數回歸曲線,消除了原序列的長期趨勢,根據對數據ADF檢驗后,發現其殘差序列為一平穩過程,最終確定ARMA預測模型。利用ARMA模型和相關統計數據可以得到農產品生產的時間序列預測數據。然后通過預測數據的增長波動指數分析并定義異常波動指標即可判斷出農產品生產異常波動的時間區域。
1.2 ARMA模型
首先,需建立自回歸模型AR(p),p階自回歸模型記作AR(p),滿足下面的方程:ut=c+φ1ut-1+φ2ut-2+…+φput-p+εt,其中:參數 c 為常數;φ1,φ2, …,φp是自回歸模型系數;p 為自回歸模型階數;εt是均值為0,方差σ2為的白噪聲序列。其次,建立移動平均模型MA(q),q階移動平均模型記作MA(q),滿足下面的方程:ut=v+εt+θ1εt-1+…θqεt-q,其中:參數 v 為常數;參數θ1,…,θq是 q 階移動平均模型的系數;εt是均值為 0,方差 σ2為的白噪聲序列,這樣就可以得到ARMA(p,q)模型:ut=c+φ2ut-1+…+φput-p+εt+θ1εt-1+…θqεt-q。當然在估計 ARMA(p,q)具體的步驟估計之前要檢驗時間序列的平穩性,特別是要檢驗其是否含有單位根及所含有的單位根的個數。
2 農產品生產預測的實證分析
為了研究的方便,以下我們以湖南糧食(水稻)為例進行農產品生產預測的實證分析,其數據來源于湖南統計年鑒,文章中的計量分析軟件采用Eviews5.0。
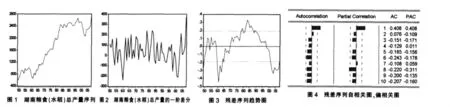
2.1 農產品產出預測模型的識別
我們首先對湖南糧食產出歷年的統計數據進行時間序列分析和一階差分分析,并將其結果描述成如圖1和圖2所示。由圖1可以看出,湖南糧食總產出總體上呈上升的趨勢,近似為一條波動向上的指數函數曲線。由圖2顯示其一階差分序列,從圖2可以看出湖南糧食總產出變化總體上呈現出頻繁波動狀態,在1997年到2008年(由于研究的起始時間為2009年,故其統計數據的選擇年限為2008年)這段時間內,出現了上下振蕩幅度較大,意味著湖南未來糧食產出波動有可能繼續延續下去的趨勢。
對于含指數趨勢的時間序列來說,我們可以通過取對數來將指數趨勢轉化為線性趨勢,即為lny,其擬合結果如下:

圖3和圖4為擬合結果的殘差序列自動生成圖形,由圖3可以看出其殘差序列基本上為一平穩序列。進一步從圖4的偏相關分析,偏相關系數在滯后一期時明顯不為0,在k>2以后都處于95%置信區間內,說明序列的偏相關函數具有截尾性,所以P可以取1;從自相關分析可知,自相關系數在滯后一期時明顯不為0,在k>2以后都處于95%置信區間內,說明序列的自相關函數具有截尾性,所以q可以取1,因此對殘差序列可以建立ARMA(1,1)模型。
2.2 農產品產出ARMA模型的建立
通過上述模型的識別,確定農產品產出ARMA(p,q)的預測模型如下:

利用統計數據通過上述模型回歸計算,得到估計方程為:


對方程進行估計后,應該對ARMA模型的適合性進行檢驗,即對模型的殘差進行自噪聲檢驗。如果殘差序列不是白噪聲序列,意味著殘差序列還存在有用信息沒被提取,需要進一步改進模型。通過對殘差序列進行ADF檢驗,其殘差序列如圖5所示。
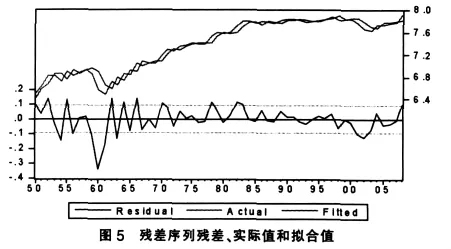
由圖5可知,首先模型的殘差序列是平穩的,說明模型通過了適應性檢驗,其次模型的擬合值與實際值保持大體一致,說明模型的預測結果可靠性也是很高的。說明指數回歸ARMA(1,1)模型的短期預測能力是非常理想的。根據2008年湖南糧食總產出為2230萬噸,這一結果與ARMA(1,1)模型的預測結果比較接近,這充分說明了ARMA(1,1)模型適用于糧食總產出中、長期預測。
2.3 農產品產出數量的預測
通過得到的回歸模型(7),將對湖南未來10年間的糧食總產量進行中長期預測,得到的結果如表1所示。
3 農產品生產異常波動的預測
首先根據表1計算湖南糧食總產出趨勢值的波動指數。所謂農產品生產波動指數指的是農產品實際產出增長率圍繞其長期趨勢上下波動的量值,它是衡量農產品生產周期波動幅度對歷史增長趨勢偏離程度的標準化指標,其波動指數的絕對值越大,說明農產品實際產出增長率偏離其長期趨勢的程度越大,農產品的產出增長越不穩定,反之,其產出增長相對穩定。其計算公式為:V=/Y,其中,=,Y=,V為波動指數,y為實際經濟增長率,Y為y的算術平均值,為標準差,n為實際值的樣本數。湖南省2009~2018年糧食產出預測值的增長波動指數值如表2。
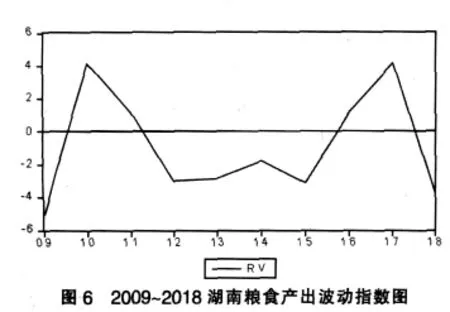
將表2描述成圖形,即為農產品生產趨勢增長波動軌跡,如圖6所示。

表1 2009~2018年湖南糧食總產出預測值 (單位:萬噸)

表2 2009~2018年湖南糧食總產出預測值的增長波動指數 (單位:萬噸)
根據圖6,我們發現從2009年至2018年以及其后的10年內,湖南糧食產出將總是處于不穩定狀態,波動幅度大,并呈逐年增大趨勢。如果將農產品生產波動指數超過3%定義為異常波動,則由表2和圖6可知,如果不考慮已經過去的2009年,則預計湖南糧食產出在未來17年時間內的2010年、2012年、2015年、2017年和2018年等5年時間可能會出現異常波動狀態。
4 研究結論
通過引進異常波動概念,運用預測模型可以對農產品生產波動趨勢的異常狀態發生的可能時間進行分析和判斷,由此政府可以利用預測信息進行農產品生產異常波動的防范行為干預,例如,儲備行為、期貨行為和政策行為等。這樣有利于促進農產品市場供求的動態均衡,有利于消除農產品生產中的“大起大落”現象,有利于降低農產品生產中蛛網現象引致的不利影響,有利于實現農產品生產的穩定增長。
[1]Mordecai Ezekiel.The Cobweb Theorem[J].The Quarterly Journal of Economics,1938,52(2).
[2]Itshak Borosh,Hovav Talpaz.Multi-Frequency Cobweb Model[J].American Journal of Agricultural Economics,1975,57(1).
[3]張淑娟,何勇.基于趨勢一狀態預測方法的糧食產量預測[J].浙江大學學報,2000,(4).
[4]張素文,李曉青.湖南省糧食生產變化趨勢及影響因子研究[J].國土與自然資源研,2005,(1).
[5]丁晨芳.組合模型分析方法在我國糧食產量預測中的應用[J].農業現代化研究,2007,(1).
[6]高鐵梅.計量經濟分析方法與建模--Eviews應用及實例[M].北京:清華大學出版社,2006.
F201
A
1002-6487(2010)22-0082-02
國家社會科學基金項目(08BJy111);湖南省社會科學基金項目(07DJ33)
羅光強(1963-),男,湖南湘鄉人,教授,博士生導師,研究方向:產業經濟。
(責任編輯/浩 天)

