p-半線性映射的性質
王喜林,劉麗紅,王 波
(吉林農業大學信息技術學院,吉林長春 130118)
p-半線性映射的性質
王喜林,劉麗紅,王 波
(吉林農業大學信息技術學院,吉林長春 130118)
首次把p半線性映射引入到線性空間,并深入研究特征p域上的線性空間p半線性映射.給出了p半線性映射的一些基本性質,包含類似線性映射的一些性質和不同于線性映射的性質.
線性空間;p-半線性映射;完備域
現在對于特征零域上的線性空間和線性映射的研究非常成熟,應用也非常廣泛,已經取得了相當系統的結果[1],于是我們開始考慮特征p域上的線性空間和p-半線性映射的情況.目前p-半線性映射在特征p域上的線性空間的應用,還處在前期的發展階段,但是它在模李代數(即特征p域上的李代數)的分類起到非常重要的作用[2].本文把特征零域上的線性空間的線性映射的一些重要性質推廣到特征p域上的線性空間,得到了p-半線性映射的一些重要性質.在此,如無另外說明,K均表示特征為p的域;V,W為K上的有限維線性空間.
定義1設K是任意一個給定的域,特征為p,其中p是一個素數.V,W是K上的線性空間.若有V到W的映射f滿足
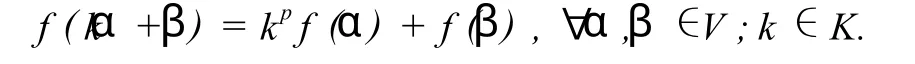
則稱f是V到W的一個p-半線性映射.即f(β)可由f(α1),…,f(αn)線性表出.


推論1設f是V到W的p-半線性映射,則f把V中等價的向量組變成W中等價的向量組.
證明設{α1,…,αs}與{β1,…,βt}是V中等價的向量組,則αi可由{β1,…,βt}線性表出,βj也可由{α1,…,αs}線性表出,i=1,…,s;j=1,…,t.由命題1知f(αi)可由f(β1),…,f(βt)線性表出,f(βj)也可由f(α1),…,f(αs)線性表出,i=1,…,s;j=1,…,t.
故{f(α1),…,f(αs)}與{f(β1),…,f(βt)}等價,即f把V中等價的向量組變成W中等價的向量組.
命題2設K是特征為p的完備域,f是V到W的p-半線性映射,則以下結論等價:
(1)f把V中的某組線性無關向量變成W中的一組線性相關向量;
(2)f把V中某非零向量變成零向量.
證明(1)?(2).設{α1,…,αs}是V中的一組線性無關的向量且滿足{f(α1),…,f(αs)}是W中的一組線性相關的向量,則存在不全為0的k1,…,ks∈K使
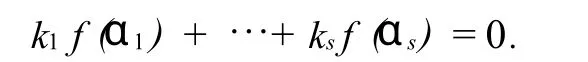
又K是特征為p的完備域,即K=Kp,故存在li∈K,i=1,…,s使得ki=lpi,i=1,…,s.則k1f(α1)+…+ks f(αs)=0,即lp1f(α1)+…+lps f(αs)=0,所以f(l1α1+…+lsαs)=0.又ki不全為0,故li不全為0.又α1,…,αs線性無關,故l1α1+…+lsαs≠0.則f把V中的非零向量l1α1+…+lsαs變成0.
(2)?(1).若有α∈V使f(α)=0,則f把V中的線性無關向量組{α}變為W中的線性相關向量組{0}.
定理1設U是V的子空間,f是U到W的p-半線性映射,則必存在V到W的p-半線性映射ɡ滿足ɡ|U=f,稱此ɡ為f的擴張.
證明設U′是U在V中的補子空間:
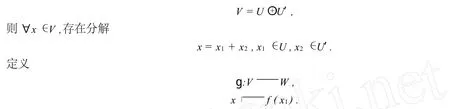
由分解唯一性知映射定義合理.則?x=x1+x2,y=y1+y2∈V,k∈K.其中:x1,y1∈U;x2,y2∈U′.有
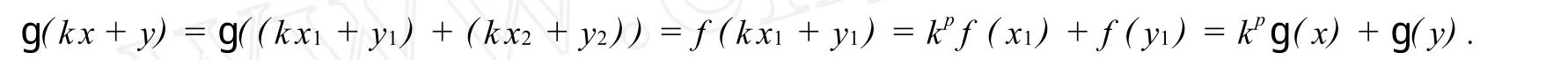
故ɡ是V到W的p-半線性映射,顯然ɡ|U=f.
命題3設f1,…,fn是V到W的互不相同的p-半線性映射,則必存在α∈V,使f1(α),…,fn(α)兩兩不相同.
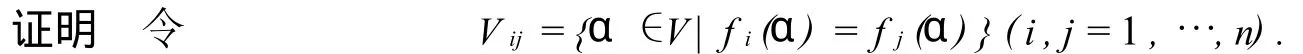
因fi(0)=fj(0)=0,故0∈V ij,又對每兩個fi,fj,存在β,使fi(β)≠fj(β),故V ij是V的真子集.
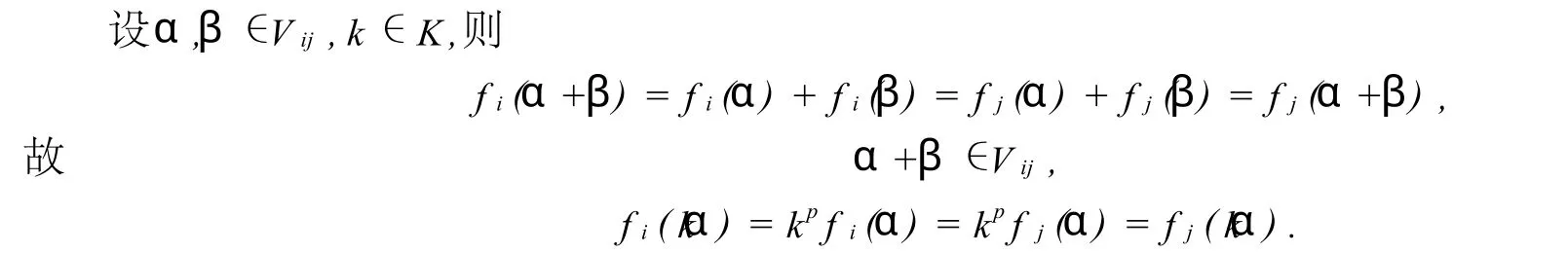
kα∈V ij,則V ij是V的真子空間.
(ⅰ)若V ij都是V的非平凡子空間,則V中至少有一個向量不屬于所有的V ij,設這個向量為α,則f1(α),…,fn(α)兩兩不同.
(ⅱ)若V ij中有V的平凡子空間V i0j0,則必有V i0j0=0,則?α≠0有fi0(α)≠fj0(α),故可不考慮這樣的V i0j0,其余的V ij便可歸結為(ⅰ)的情形.
定義2設f是V到W的p-半線性映射,f的核定義為

命題4設f是V到W的p-半線性映射,則以下結論成立:
(1)f是單射?Kerf={0};
(2)f是滿射?Cokerf={0}.
證明
(1)若f是單射,則只存在一個α∈V,使f(α)=0.但f(0)=0,故α=0,則Kerf={0}.
反之,設Kerf={0}.若有α,β∈V,使f(α)=f(β),則f(α-β)=f(α)-f(β)=0,故α-β∈Kerf={0},則α=β,f是單射.
(2)f是滿射?Imf=W?W/Imf={0}?Cokerf={0}.
定理2設f是V到V的p-半線性映射,K是完備域(即K=Kp),則有
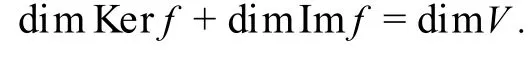

則f(es+1),…,f(en)是Imf的生成元,下面證明它們線性無關.
否則,若它們線性相關,則存在不全為0的ls+1,…,ln∈K滿足
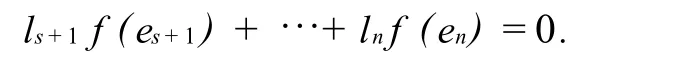
因K=Kp,故存在hs+1,…,hn∈K,滿足hpi=li,i=s+1,…,n,則有f(hs+1es+1+…+hn en)=0,故
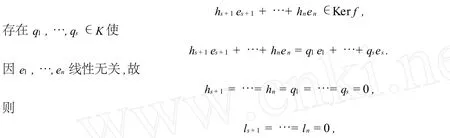
產生矛盾.故f(es+1),…,f(en)線性無關,并且是Imf的基,dim Imf=n-s=dimV-dim Kerf.
定理3設f是V到V的p-半線性映射,K是完備域(即K=Kp),則f是單射?f是滿射.
由命題4和定理2知,f是單射?Kerf=0?dim Imf=dimV?Imf=V?f是滿射.
定理4設f是V到V的p-半線性映射,K是完備域(即K=Kp),且dim Imf=r.則存在V到V的p-半線性映射f1,…,fr滿足條件dim Imfi=1,i=1,…,r,且使得

證明不妨設dimV=n.因dim Imf=r,故dim Kerf=n-r.在Kerf中取基α1,…,αn-r,擴充為V的基α1,…,αn-r,β1,…,βr.由定理2的證明過程知f(β1),…,f(βr)是Imf的基.?j∈{1,…,r}構造fj: V→V為
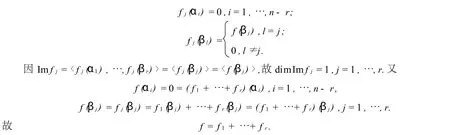
定義3設f是V到V的p-半線性映射,U是V的子空間.若對于任意的向量α∈U,都有f(α)∈U,就稱U是p-半線性映射f的不變子空間,簡稱f-子空間.
例3f-子空間的和與交仍是f-子空間.
證明設V1,V2是V的f-子空間,下面證明V1+V2,V1∩V2是f-子空間.
易知V1+V2,V1∩V2是V的子空間.
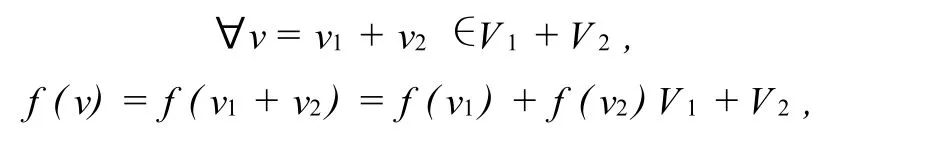
故V1+V2是f-子空間.
?v∈V1∩V2,則v∈V i,i=1,2.故f(v)∈V i,i=1,2,則f(v)∈V1∩V2,且V1∩V2是f-子空間.
命題5設f是V到V的p-半線性映射,U是V的子空間,e1,…,es是U的一組基,則
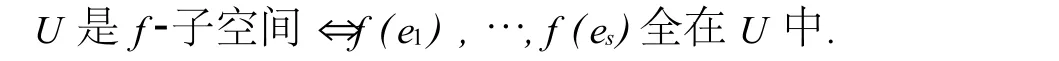
證明充分條件顯然.下證必要條件.

[1] WERNER GREUB.Linear algebra[M].New York:Sp ringer,2009:1-185.
[2] STRADE H,FARNSTEINER R.Modular Lie algebras and their rep resentations[M].New Yo rk:Marcel Dekker Inc, 1988:300.
On the properties of p-sem ilinear mapping
WANG Xi-lin,L IU Li-hong,WANGBo
(College of Information and Technology,Jilin Agricultural University,Changchun 130118,China)
In this paper,the definition onp-semilinearmappings for linear spaces is first introduced and ap-semilinear mapping is investigated.Some elementary p ropertiesofp-semilinearmapings are given, w hich contain the same p roperties to linear mappings and the different p roperties from linear mappings.
linear spaces;p-semilinear mappings;perfect field
O 152.5
110·2125
A
1000-1832(2010)04-0021-05
2010-08-10
國家自然科學基金資助項目(10871057).
王喜林(1973—),男,碩士,講師,主要從事代數研究;通訊作者:劉麗紅(1975—),女,碩士,講師,主要從事代數研究;王波(1973—),女,博士,副教授,主要從事線性代數和數量經濟研究.
(責任編輯:陶 理)

