冪群的等價(jià)條件及其性質(zhì)的研究

張朝鳳,王連平

(1.吉林大學(xué)數(shù)學(xué)中心,吉林長春 130012; 2.吉林大學(xué)計(jì)算機(jī)中心,吉林長春 130012)

冪群的等價(jià)條件及其性質(zhì)的研究

張朝鳳1,王連平2

(1.吉林大學(xué)數(shù)學(xué)中心,吉林長春 130012; 2.吉林大學(xué)計(jì)算機(jī)中心,吉林長春 130012)

在冪群概念及已有性質(zhì)的基礎(chǔ)上,給出了循環(huán)群冪群、一般冪群的等價(jià)條件,并給予了嚴(yán)格的證明.提出了冪群的一些新的性質(zhì),得到了一些有意義的結(jié)論.

冪群;循環(huán)冪群;等價(jià)關(guān)系

1 預(yù)備知識(shí)

本文始終假定(G,·)是一個(gè)群.在P(G)-{Φ}中規(guī)定代數(shù)運(yùn)算[1]:

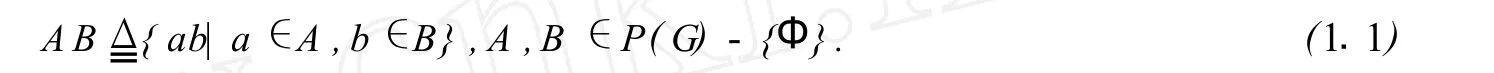
取非空集類g?P(G)-{Φ},如果g關(guān)于運(yùn)算(1.1)做成群,則稱g為G上的一個(gè)冪群.其單位元用E表示.

特別稱g是G上的一個(gè)正則冪群,如果e∈E,這里e是G的單位元.

定理1.1[2-4](基數(shù)定理)設(shè)g是群G上的冪群,則對(duì)任意一個(gè)A∈g,有|A|=|E|.若g是群G的冪群,置是半群.

設(shè)E是G的含單子半群,稱E是G的正規(guī)子半群,如果E滿足條件:對(duì)任意x∈G,有x E=Ex.

定義1.1[5]設(shè)E是G的正規(guī)子半群,則{x E|x∈G}是G的冪群,稱為G的廣義商群.

2 循環(huán)群的冪群的等價(jià)條件

設(shè)G=〈a〉是循環(huán)群,A={aj1,aj2,…,ajn,…}∈G,且A中列出的元素兩兩互異,則稱Ap={j1, j2,…,jn,…}為A的指數(shù)集,稱A為A p相應(yīng)的元素集.

取g?P(G)-{Φ},記gp={Ap|A∈g}.

設(shè)m為正整數(shù),X為一整數(shù)集,且對(duì)任意a,b∈X,a≠b(modm),則稱X為關(guān)于m的非同余數(shù)集.

設(shè)m為正整數(shù),X,Y都是關(guān)于m的非同余數(shù)集.如果對(duì)每個(gè)a∈X,有b∈Y,使a≡b(modm),且對(duì)每個(gè)d∈Y,有c∈X,使d≡c(modm),則稱X與Y是關(guān)于m的等價(jià)組.記為X≡Y(modm).

注2.1如果X與Y是關(guān)于m的等價(jià)組,則有|X|=|Y|.

注2.2如果X與Y是關(guān)于m的等價(jià)組,則稱X與Y關(guān)于m有關(guān)系“～”,顯然“～”是整數(shù)集間的等價(jià)關(guān)系.

設(shè)G=〈a〉是循環(huán)群[6-8],g?P(G),g≠?,定義g的指數(shù)冪集的子集gp中的加法[3]:

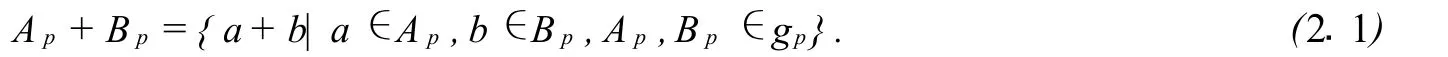
命題2.1設(shè)G=〈a〉為有限循環(huán)群,且o(G)=m,g是G上冪集的子集,則g是冪群的充要條件是gp滿足如下條件:

(1)對(duì)任意Ap,Bp∈gp,存在Cp∈gp,使Ap+Bp≡Cp(modm);

(2)存在Ep∈gp,使得對(duì)任意Ap∈gp,有Ap+Ep≡Ap(modm);

(3)對(duì)任意Ap∈gp,存在Bp∈gp,使Ap+Bp≡Ep(modm).

證明必要性:如果g是G上冪群,則對(duì)任意Ap,Bp∈gp,考慮相應(yīng)的元素集A,B,則有C∈g,使C=AB,于是有Cp∈gp,使Cp≡Ap+Bp(modm).

事實(shí)上,?s∈Cp,有as∈C且as=ak·al,其中ak∈A,al∈B,即s≡k+l(modm);反過來,對(duì)任意k′+l′∈Ap+Bp,有ak′+l′∈AB=C,故有as′∈C,使ak′+l′=as′,從而k′+l′≡s′(modm),條件(1)得證.

與上面的討論類似,可由群的單位元的存在性,推知條件(2)被滿足;可由群的逆元的存在性推知條件(3)被滿足.

充分性:如果g的指數(shù)冪集的子集gp滿足條件(1)—(3),則:

(ⅰ)對(duì)任意A,B∈g考慮A和B的指數(shù)集Ap和Bp.由條件(1),存在Cp∈gp,使Ap+Bp≡Cp(modm).這樣,?ai∈A,aj∈B,存在k∈Cp,使i+j≡k(modm),相應(yīng)的有ai+j=ai·aj=ak∈C;而?ak′∈C,應(yīng)有i′∈Ap,j′∈Bp,使i′+j′≡k′(modm),即有ai′∈A,aj′∈B,使ak′=ai′+j′=ai′·aj′,即得到C∈g,使AB=C∈g,g對(duì)乘法封閉.

(ⅱ)由條件(2)中Ep的存在性,同條件(ⅰ)的討論類似,可證明g中與Ep相對(duì)應(yīng)的元素E∈g即為g的右單位元.

(ⅲ)?A∈g,由條件(3),考慮A的指數(shù)集A p,知有Bp∈gp,使Ap+Bp≡Ep(modm),則同(ⅰ)的討論類似,可知與Bp相對(duì)應(yīng)的B∈g即為A在g中的右逆元.

綜合(ⅰ)—(ⅲ)可得g為G上冪群.

注2.3顯然(2.1)式中定義的加法可交換,并由此可知命題2.1的條件(1)—(3)中做和的兩項(xiàng)可交換.

命題2.2有限循環(huán)G的階為m,那么G上的冪群(g,·)與(gp,+)同態(tài),因而(gp,+)為整數(shù)加群中的冪群.

則由gp的定義即知φ是g到gp的滿射.

又對(duì)A,B∈g,由基數(shù)定理可設(shè)

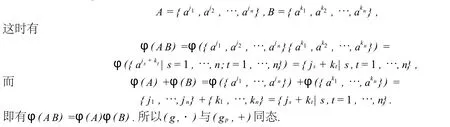
推論2.1有限循環(huán)群冪集的子集g關(guān)于運(yùn)算(1.1)所給的乘法做成冪群的充要條件是g的指數(shù)集的子集gp關(guān)于整數(shù)集類的等價(jià)系(可視為相等關(guān)系),在運(yùn)算(2.1)所給的加法下做成(整數(shù)集類的)冪群.

與命題2.2的討論類似,我們立刻可得下面的命題.

命題2.3設(shè)G=〈a〉為無限循環(huán)群,g?p(G)-{?},則g關(guān)于運(yùn)算(1.1)給出的乘法做成冪群的充要條件是gp滿足:

(1)對(duì)任意Ap,Bp∈gp,存在Cp∈gp,使Ap+Bp=Cp;

(2)存在Ep∈gp,使對(duì)任意Ap∈gp,有Ap+Ep=Ap;

(3)對(duì)每個(gè)Ap∈gp,都存在Bp∈gp,使Ap+Bp=Ep.

命題2.4設(shè)G為無限循環(huán)群,G上的冪群(g,·)與g指數(shù)冪集的子集gp關(guān)于運(yùn)算(2.1)中加法做成的有運(yùn)算集(gp,+)同構(gòu).

推論2.2無限循環(huán)群冪集的子集g,關(guān)于運(yùn)算(1.1)所給的乘法做成冪群的充要條件是g的指數(shù)冪集gp關(guān)于運(yùn)算(2.1)所給的加法做成冪群.

3 一般冪群的等價(jià)條件

定義3.1設(shè)G是群,g?p(G)-{?},對(duì)于A,B∈g,如果存在C∈g,使AC=B,則稱A在g中可經(jīng)C右傳遞到B,簡稱A(在g中)可右傳到B.記為A～CB.如果存在D∈g,DA=B,則稱A在g中可經(jīng)D左傳遞到B,簡稱A可左傳到B.記為AD～B.如果A既可左傳到B,亦可右傳到B,則A可傳到B,記為A～B.

如果?A,B,C∈g,A～B D,AC～K時(shí)總有D,K∈g,則稱g為關(guān)于運(yùn)算(1.1)中乘法的傳遞閉包,簡稱g為一個(gè)傳遞閉包.

命題3.1設(shè)G是群,g?p(G)-{?},則g是關(guān)于運(yùn)算(1.1)中乘法的傳遞閉包的充要條件是?A,B,C∈g,都有AB,CA∈g.

命題3.2 設(shè)G是群,g0?p(G)-{?},令

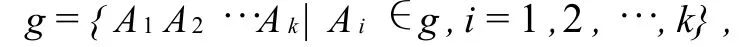
命題3.5設(shè)G是群,g?p(G)-{?},g是G上一個(gè)冪群,當(dāng)且僅當(dāng)以下條件滿足:

(1)g是關(guān)于運(yùn)算(1.1)中乘法的傳遞閉包;

(2)?A∈g,A都可經(jīng)g中同一元E右傳遞到A;

(3)對(duì)每個(gè)A∈g,A都可右傳遞到E.

證明(ⅰ)如果g是G上冪群,則?A,B和C∈g,由命題3.1知AB和CA∈g,從而g為一個(gè)傳遞閉包.

(ⅱ)g中存在單位元E,使?A∈g,有A E=A,即A～E A,也即g中任一元A都可經(jīng)g中同元右傳到本身.

(ⅲ)對(duì)每個(gè)A∈g,存在A-1∈g,使AA-1=E,即A～A-1E,亦即A總可右傳遞到E.反之,如果g?p(G)-{?},且滿足條件(1)—(3),則:

(ⅰ)對(duì)A,B∈g,由命題3.1,總有AB∈g,故g對(duì)乘法封閉;

(ⅱ)因g中每一元都可經(jīng)同元E右傳遞到本身,即對(duì)A∈g,有A～EA,A E=A成立.故E為g中右單位元;

(ⅲ)因?qū)γ恳籄∈g,有B∈g,使A～B E,即AB=E,所以每一元A∈g都有右逆元,即g為關(guān)于運(yùn)算(1.1)乘法的冪群.

注3.1顯然,將命題3.5中條件(2)和(3)里的“右”全改為“左”,命題3.5的結(jié)論不變.若將條件(2)和(3)里的“右”全刪去,命題的結(jié)論亦成立.

定義3.2設(shè)G是群,g?p(G)-{?},稱

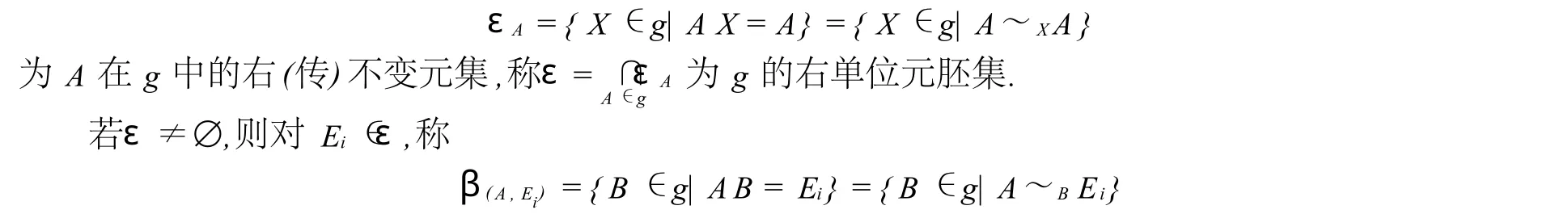
為A在g中關(guān)于Ei的右可除元集.

如果對(duì)一切A∈g,β(A,Ei)≠?,那么稱Ei為g的一個(gè)右單位元;稱β(A,EI)中元A為q的右逆元.由群論知識(shí)可知,g的右單位元即g的左單位元,也即g的單位元,且唯一.又g的一個(gè)元的右逆元,即它的左逆元,也即它的逆元,且唯一.

命題3.6設(shè)G是群,g?p(G)-{?}是G上的冪群,當(dāng)且僅當(dāng)以下條件被滿足:

(1)g是關(guān)于運(yùn)算(1.1)中乘法的傳遞閉包;

反之,如果G上g?p(G)-{?},且g滿足條件(1)—(3),則顯然g對(duì)運(yùn)算(1.1)的乘法封閉.

又因?yàn)榇嬖贓i∈ε,使每個(gè)A(A∈g)的右可除元集β(A,Ei)≠?,故Ei即是g對(duì)運(yùn)算(1.1)中乘法的單位元.事實(shí)上,對(duì)每個(gè)A∈g,因Ei∈εA,有A Ei=A.

再由β(A,Ei)≠?,知存在B∈g,使AB=Ei,這就證得g為G上的冪群.

(2)g的右單位元胚集ε≠?;

(3)對(duì)g存在Ei∈ε,使得每個(gè)g中元A的右可除元集β(A,Ei)≠?.

證明如果g是G上的冪群,則條件(1)顯然被滿足.又由g中存在單位元E,故對(duì)每一個(gè)A∈g,有

4 其他性質(zhì)

命題4.2設(shè)G為一個(gè)群,g是G的冪群,E是g的單位元.如果e∈A?g,則總有A-1?E?A.

由命題4.1的證明,知E?A.且E=AA-1=[E∪(A|E)]A-1=A-1∪(A|E)A-1,即得A-1?E.

[1] 李洪興,汪培莊.冪群[J].應(yīng)用數(shù)學(xué),1988(Z1):1-4.

[2] L IHONG XING.HX group[J].BUSEFAL,1987,33:31-37.

[3] L IHONG XING.HX group[J].BUSEFAL,1988,34:14-17.

[4] 李洪興.正則HX群的同態(tài)與同構(gòu)[J].模糊系統(tǒng)與數(shù)學(xué),1990,4(1):1-7.

[5] 何清,李洪興.冪群的表示與同構(gòu)的提升[J].北京師范大學(xué)學(xué)報(bào):自然科學(xué)版,1999,35(1):32-37.

[6] 張禾瑞.近世代數(shù)基礎(chǔ)[M].北京:高等教育出版社,1998:60-101.

[7] M·赫爾.群論[M].裘光明.北京:科學(xué)出版社,1981:40-87.

[8] 劉曉蕾,王燕鳴.有限群的p-冪零性的一個(gè)注記[J].吉林大學(xué)學(xué)報(bào):理學(xué)版,2009,47(3):523-526.

The equal value requirement and nature of power group

ZHANG Chao-feng1,WANG Lian-ping

(1.Centre of Mathematics,Jilin Univesity,Changchun 130012,China; 2.Centre of Computer,Jilin Univesity,Changchun 130012,China)

On the basis of the pow er group concep t and the exited nature,this thesis w ill further put forw ard some equal value requirement for the power group of cycle group and the general power group.Furthermore,this thesis has p roved strictly and puts forward some other natures of power group.Therefore,some meaningful conclusions have been obtained.

power group;power group of cycle;equivalence relation

O 152

110·2115

A

1000-1832(2010)04-0026-04

2010-08-20

國家自然科學(xué)基金資助項(xiàng)目(10871057).

張朝鳳(1962—),女,副教授,主要從事代數(shù)理論研究.

(責(zé)任編輯:陶 理)