端部初始燃面可變的星孔火箭裝藥燃燒特性

牛公杰，錢建平，劉榮忠

（南京理工大學機械工程學院，江蘇 南京210094）

引 言

傳統的小型自由裝填式固體火箭發動機在設計時，為了控制藥柱的燃燒面積，通常用包覆層將藥柱的部分表面進行包覆［1］。根據所設計的裝藥結構幾何尺寸，按照平行層燃燒理論可準確地計算出燃燒過程中不斷變化的燃面面積，進而計算出火箭發動機內彈道諸元。對于采用星孔裝藥的小型自由裝填式固體火箭發動機，常用的包覆措施是將藥柱側面、上、下端面包覆；但也有采取僅將藥柱側面包覆，而上下端面不包覆的方法，通過藥柱端面和墊片間的間隙使藥柱端面在火箭發動機工作過程中也參與燃燒，進一步提升火箭發動機性能［2］。

星孔火箭裝藥的端部初始燃燒面積對火箭發動機性能有著重要影響。而間隙的大小又決定了端部初始燃面的變化規律。裝藥端部參與燃燒雖然有助于提升火箭發動機性能，但也給端部初始燃面的計算帶來困難，無法使用經典的燃面計算理論進行描述和計算［3］。本研究通過引入端面燃燒參與度和端面等效燃燒厚度的方法來解決燃面計算問題，并結合試驗條件推導出了燃面面積經驗計算公式，得出溫度對火箭發動機性能的影響規律和可用于指導實際工程應用的結論。

1 燃面計算方法

1.1 基本假設

火箭發動機裝藥在點火具作用下，藥柱星孔全面瞬時點燃，高溫燃氣和火焰會竄入藥柱端面和墊片之間的間隙并逐漸點燃端面，過程較為復雜，難以用量化的方式描述，應用傳統的燃面計算理論無法描述燃面變化規律和計算燃面面積，需引入新的方法解決燃面計算問題。

根據藥柱燃燒特點，可將燃面計算過程分為星孔燃面面積計算和端部燃面面積計算兩部分，并作如下假設：（1）在點火壓強作用下星孔全面瞬時點燃；（2）忽略藥柱的侵蝕燃燒效應；（3）星孔燃燒遵循平行層燃燒定律，燃面沿起始表面各點的法線向內部推移。

對于星根圓角化的星孔裝藥，星孔燃燒過程可分為4個階段［4］，即：（1）星根圓角消失前，星邊周邊長為s1，單位：m；（2）星邊消失前，星邊周邊長為s2，單位：m；（3）星邊消失后，星邊周邊長為s3，單位：m；（4）余藥階段燃燒階段，星邊周邊長為s4，單位：m。

圖1為星孔裝藥結構示意圖。其中左側為星孔藥柱端面燃燒示意圖，右側為藥柱沿軸向的剖面圖。端部燃燒是個極其復雜的過程，為簡化計算，作如下4點假設：（1）藥柱燃燒到t時刻時，一個端面的總面積為Stt，單位：m2，且：Stt=πD2／4-Ap，D為藥柱外徑，單位：m，Ap為藥柱星孔通氣面積，單位：m2；（2）藥柱燃燒到t時刻時，一個端面參與燃燒的面積為Stb，單位：m2，并且假設燃面Stb平行于藥柱初始端面；（3）引入端面燃燒參與度α，表示一個端面當前參與燃燒的面積Stb與當前端面總面積Stt之比，即：且0≤α≤1；（4）根據藥柱質量守恒原則，引入端面等效燃燒厚度et，單位：m。

1.2 端面燃燒參與度α

藥柱端面和墊片之間的間隙是影響α變化過程的主要因素。發動機的零件加工誤差和裝配誤差直接影響藥柱端面與墊片間初始間隙的大小，而溫度變化則會改變初始間隙的大小。一般發動機殼體的熱膨脹系數遠小于藥柱的熱膨脹系數，而墊片的厚度與發動機藥室高度和藥柱高度相比很小，故當發動機殼體、藥柱和墊片三者經歷相同的溫度變化后，藥柱高度變化量要遠大于發動機藥室高度變化量和墊片高度變化量，所以間隙的變化主要取決于藥柱的高度變化量。以發動機在常溫狀態下裝配產生的間隙為基準，當發動機在高溫狀態下，間隙變小，在低溫狀態下，間隙變大。

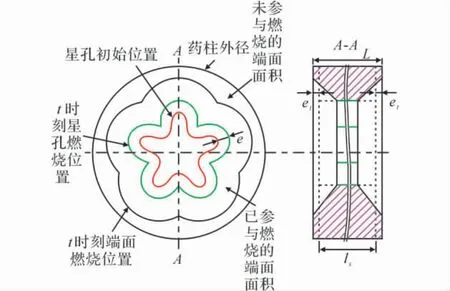
圖1 星孔裝藥結構示意圖Fig.1 Schematic diagram of star shaped rocket grain

從定性的方面分析，藥柱端面與墊片之間的間隙越大、燃燒室壓強p越大、藥柱初始溫度越高、藥柱的長徑比L／D越大，則端面點燃速度越快，端面全面參與燃燒所用的時間越短，反之亦然。因藥柱端面隨著藥柱燃燒時間的增加而逐漸點燃，選取時間t為自變量，考慮到α的變化過程與藥柱燃燒室壓力p、藥柱長度L、初始溫度T、藥柱直徑D等因素密切相關，α可表示為：

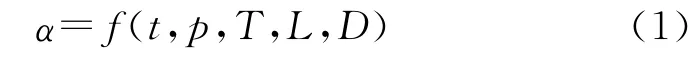
根據試驗，發現對于長徑比在1.3左右、特征長度與肉厚比在0.5左右、星角數為5的星孔裝藥，其端面正常逐漸參與燃燒時，α呈冪函數形式變化。研究結合試驗條件和測試結果，推導出了不同情況下α的經驗計算公式。

（1）常溫和低溫情況下，藥柱端面在點火初始時刻即可正常參與燃燒的經驗公式為：

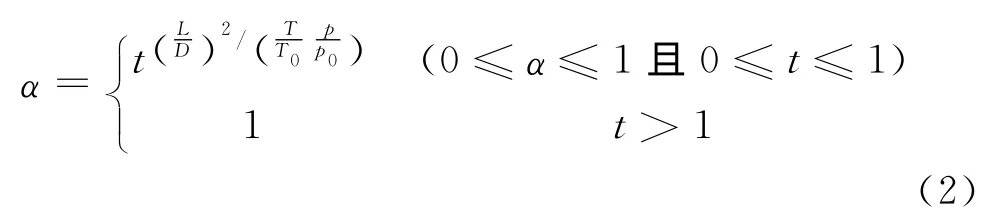
式中：t為燃燒時間，s；T為藥柱初始溫度，K；T0為參考基準溫度，K，T0=273.15K；p0為參考基準壓力，Pa，p0=106Pa。

（2）高溫情況下，由于藥柱端面與墊片的間隙變小或消失，初期燃燒室內壓力相對較小，燃氣不能順利與端面接觸，藥柱端面在初始燃燒階段燃燒參與程度較小，當燃燒進行到某一臨界時刻t0（t0＜1），燃燒室內壓強升高到某一個臨界值時，燃氣急劇竄入間隙，迅速全面點燃尚未參加燃燒的端面，α的經驗公式為：

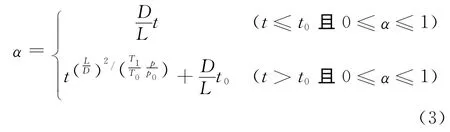
式中：t0為臨界時刻，s，其大小根據具體試驗條件確定。

1.3 端面等效燃燒厚度et

由于端面燃燒參與度系數α的引入，為保證藥柱燃燒質量守恒，需將端面燃燒厚度做等效處理。在端面從起始燃燒到全面燃燒的過程中，即當0≤α＜1時，設在dt時間微元內一個端面燃燒掉的質量微元為dmt，它應該等于當前時刻的端面參與燃燒的燃燒面積Stb、燃燒厚度微元de和推進劑密度ρp三者的乘積，即：

式中：mt為端面燃燒掉的質量，單位：kg。

將質量微元dmt等效由當前端面面積為燃面燒去的質量，則質量微元dmt應等于當前端面面積Stt、端面等效燃燒厚度微元det和推進劑密度ρp三者的乘積，即：

根據（4）、（5）兩式相等，可導出端面等效燃燒厚度et的微分方程：

記端面面積全部參與燃燒瞬時時刻為tα1，當t≥tα1時，端面面積全部參與燃燒，Stb=Stt，α=1。

式中：a為燃速系數，m／（s·Pan）；n為燃速指數。

由（7）式即得到端面等效燃燒厚度計算公式

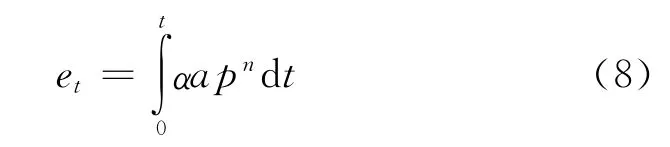
1.4 總燃面計算

總燃面面積應等于星孔燃面面積加上端部燃面面積。星孔燃面面積根據平行層燃燒定律計算，藥柱星孔長度應等于藥柱初始長度L減去兩個端面的等效燃燒厚度2et，則星孔燃面面積計算公式：

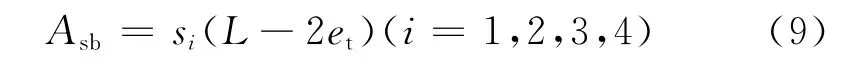
式中：Asb為星孔燃面面積，m2；i=1，2，3，4，對應4個燃燒階段。

將Stt=πD2／4-Ap代入上式即得端面燃燒面積計算公式

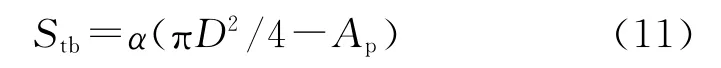
則總燃燒面積：

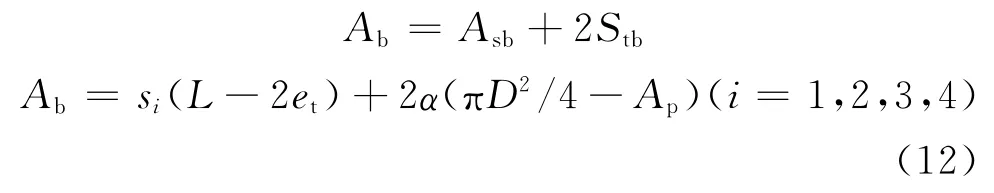
式中：Ab為總燃面面積，m2。

2 結果與分析

在相同的室溫條件下完成9 發火箭發動機的裝配，放入保溫箱保溫。試驗分常溫、低溫和高溫試驗3組，每組試驗3發，取3次試驗數據的平均值作為每組的試驗結果。采用零維火箭內彈道計算方法［5］，利用計算機采用四階龍哥庫塔法編程求解火箭內彈道方程。考慮到固體火箭發動機在工作時可能出現兩種端部初始燃面恒定的極端工作狀態：（1）藥柱端面不參與燃燒，端部初始燃面面積為零；（2）藥柱端面在發動機工作開始時刻全面瞬時點燃。所以計算時采用3 種燃面計算方法：（1）星孔全面瞬時點燃，上端面、下端面不參與燃燒；（2）星孔、上端面、下端面全面瞬時點燃參與燃燒；（3）星孔全面瞬時點燃、上端面、下端面逐漸點燃參與燃燒。

火箭裝藥為某雙基型推進劑，藥柱密度ρp=1.612g／cm3，火藥力f=929 000J／kg，燃氣絕熱指數k=1.225，不同溫度條件下的a、n值見表1。

表1 不同溫度條件下的a、n值Table 1 The value of aand nat different temperatures

2.1 常 溫

試驗溫度為+15℃，藥柱初始溫度為288.15K，α采用公式（2）計算。表2為火箭發動機性能特征量的試驗值和計算值，得到的燃燒室頭部p-t曲線見圖2。

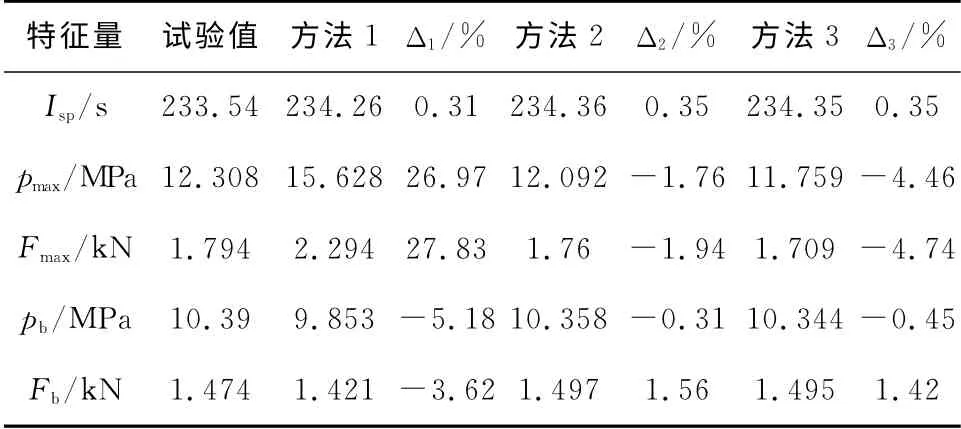
表2 +15℃時發動機特征量的試驗值與計算值Table 2 Experimental and calculated results at of characteristic values of motor+15℃

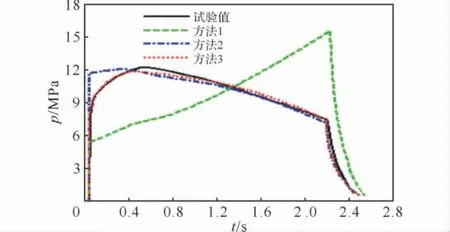
圖2 +15℃時燃燒室頭部的p-t曲線Fig.2 The p-t curves of chamber head at+15℃

從表2可以看出，方法1在最大壓強和最大推力方面的相對誤差分別高達26.97%和27.83%，理論值與試驗值相差甚遠；而方法2和方法3計算出的各項特征量相對誤差均小于5%。

試驗測試數據處理時剔除了試驗測試曲線的初始壓強峰。從圖2可以看出，方法1計算得出的p-t曲線與試驗明顯不符，原因是燃燒過程中只有星孔參與燃燒，星孔的初始燃面面積小，導致初始階段壓強較試驗值小，隨著星孔燃面面積不斷增大，壓強也逐漸增大，壓強呈上升趨勢，與實際情況不符；方法2計算得出的p-t曲線在藥柱初始燃燒階段明顯高于試驗測試曲線，原因是方法2采用的是星孔和兩端面瞬間全部點燃，初始燃面面積較大，致使初始階段燃燒壓力較高；方法3計算得到的p-t曲線僅在0.5～1.0s時間內稍低于試驗測試曲線，其余部分與試驗曲線基本吻合，特別是初始燃燒階段吻合較好。

2.2 低 溫

試驗溫度為+15℃，藥柱初始溫度T為233.15K，α采用公式（2）計算。火箭發動機性能特征量試驗值和計算值見表3，發動機燃燒室頭部p-t曲線，見圖3。

從表3可以看出，方法1在最大壓強和最大推力方面的相對誤差分別高達27.53%和28.66%，誤差較大；而方法2和方法3計算出的各項特征量相對誤差均小于5%。

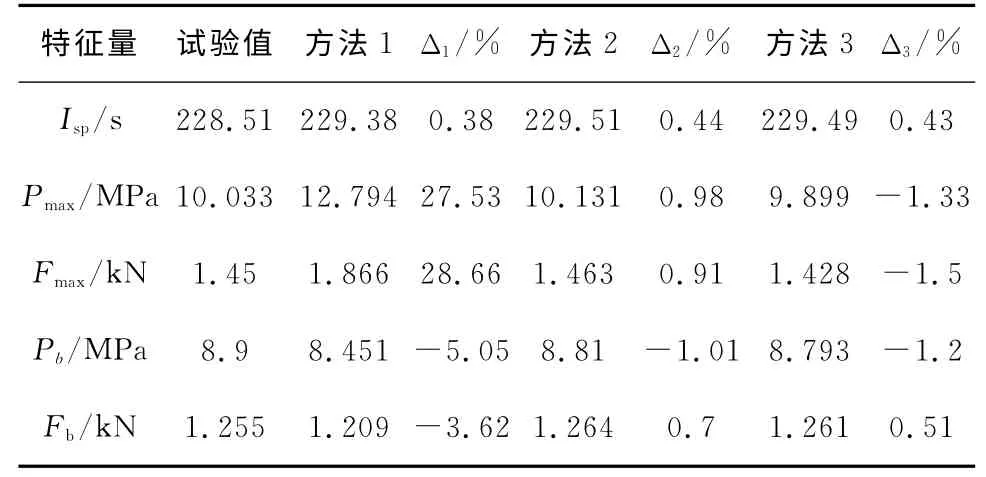
表3 -40℃時發動機特征量的試驗值與計算值Table 3 Experimental and calculated results of characteristic values of motor at-40℃

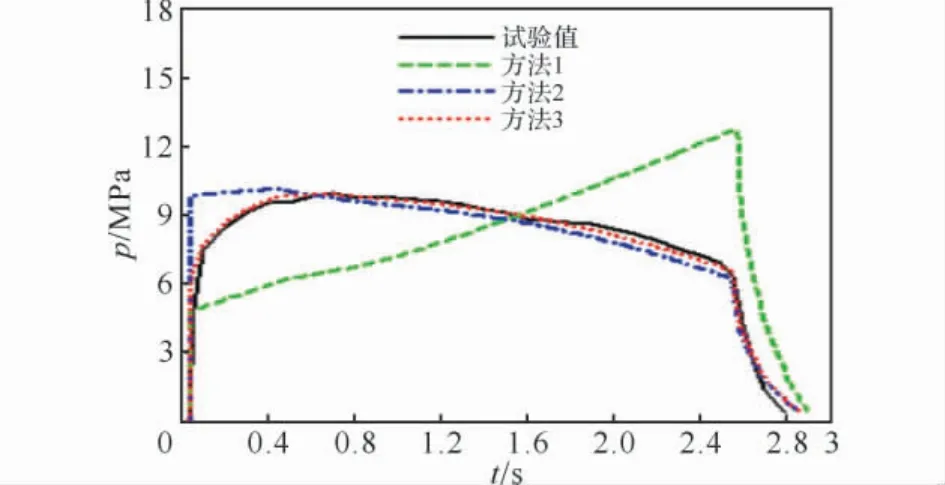
圖3 -40℃時燃燒室頭部的p-t曲線Fig.3 The p-t curves of chamber head at-40℃

圖3中，用方法1計算出的p-t曲線與試驗曲線明顯不符；用方法2計算出的p-t曲線在藥柱初始燃燒階段明顯高于試驗測試曲線，而在后期又明顯低于試驗測試曲線；用方法3計算出的p-t曲線在整個燃燒過程中與試驗曲線吻合較好，計算曲線和試驗曲線均比較平滑。

2.3 高 溫

試驗溫度為+50℃，藥柱初始溫度T為328.15K，α采用公式（3）計算，根據試驗結果，取t0為0.5s。火箭發動機性能特征量試驗測試和理論計算結果見表4，發動機燃燒室頭部的p-t曲線見圖4。

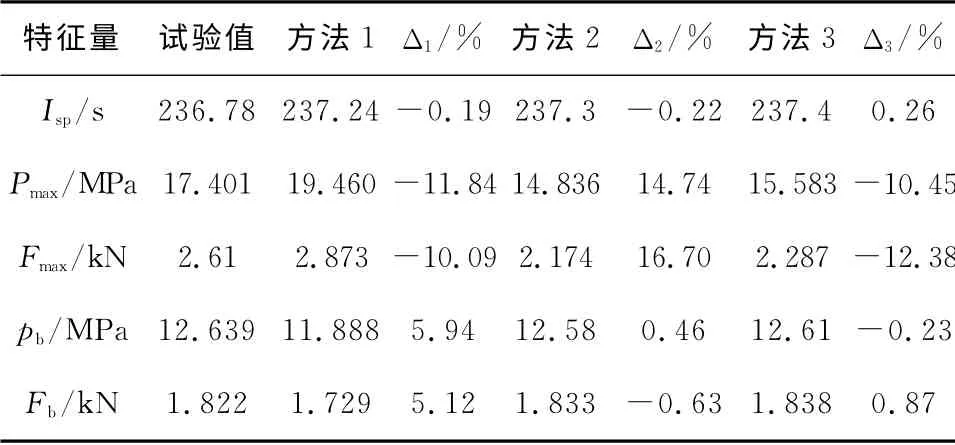
表4 +50℃下試驗測試與理論計算結果Table 4 The experimental test and calculated results of characteristic value of motor at+50℃

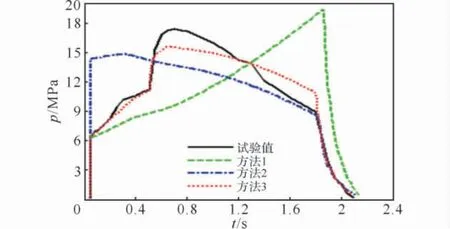
圖4 +50℃時燃燒室頭部的p-t曲線Fig.4 The p-t curves of chamber head at+50℃

從表4和圖4可以看出，用方法1和方法2計算出的p-t曲線與試驗曲線相差甚遠，無法對火箭發動機性能進行有效預示，用方法3計算出的曲線在初始階段與試驗吻合較好，但在0.5s以后的曲線上升段和后期吻合不夠理想。在常溫下將火箭藥柱裝入發動機藥室，令藥柱的一端無約束，在+50℃條件下保溫48h后，藥柱沿軸向伸長0.58mm，火箭藥柱在高溫狀態下受熱膨脹，致使藥柱端面與墊片間的間隙變小或消失，導致在初始燃燒階段藥柱端面正常參與燃燒，p-t曲線在初始階段上升緩慢；但隨著燃燒進行到大約0.5s，燃燒室壓力升高到11MPa左右時，高溫燃氣開始急劇竄入藥柱端面和墊片之間的間隙，點燃尚未參加燃燒的端面部分，總燃面面積突然增大，致使燃燒室壓強陡然升高。

藥柱在高溫條件下受熱膨脹伸長量若過大，嚴重時可使藥柱端面、墊片和發動機壁面三者處于受壓狀態，間隙消失，使藥柱端面不能正常燃燒，同時又使藥柱內部產生應力，過大的應力又可誘發藥柱表面或內部產生裂紋，甚至發生破碎，導致火箭發動機工作異常。燃燒室壓強階躍式升高很可能會破壞火箭發動機的結構，應避免此種情況的發生［6］。在火箭發動機裝配時，藥柱和墊片在軸向方向上要保留適當的間隙或加入間隙調節裝置，以保證火箭發動機在高溫條件下正常工作。

此外，在常溫、低溫和高溫下，用方法3計算的藥柱燃燒質量均為1.444kg，與藥柱實際質量1.445kg接近，相對誤差僅為-0.07%。

3 結 論

（1）在常溫和低溫條件下，星孔裝藥端面是以逐漸參與燃燒的方式進行燃燒，試驗中可得到較為平滑的p-t曲線；而裝藥端面不參與燃燒和裝藥端面瞬時全面參與燃燒的方式與實際情況不符。

（2）通過引入端面燃燒參與度和端面等效燃燒厚度的方法，并結合試驗條件推導出燃面面積經驗計算公式，解決了藥柱在燃燒過程中的燃面計算問題。在常溫和低溫條件下，計算值與試驗值的相對誤差均小于5%，計算得到的p-t曲線與試驗曲線基本吻合；高溫條件下稍顯不足。

（3）采用上、下端面均無包覆星孔裝藥的火箭發動機工作穩定性受溫度影響較大。藥柱端面和墊片之間要留有適當的間隙或加入間隙調節裝置，間隙大小可根據火箭發動機的具體藥型尺寸和試驗測試結果調整。

（4）端面燃燒參與度和端面等效燃燒厚度的引入提供了一種解決端部初始燃面可變的星孔火箭裝藥燃面計算問題的方法，可為同類固體火箭發動機內彈道性能預測提供參考。

［1］侯林法，楊忠雄.復合固體火箭推進劑［M］.北京：中國宇航出版社，1994.

［2］夏志全.端面燃燒發動機研制中應注意的幾個問題［J］.固體火箭技術，2000，23（2）：12-15.

XIA Zhi-quan.Several problems for end burning solid motor development［J］.Journal of Solid Rocket Technology，2000，23（2）：12-15.

［3］許鵬，梁景媛，梁國柱，等.固體火箭發動機裝藥端面燃燒燃速畸變現象分析［J］.火炸藥學報，2006，29（5）：32-34.

XU Peng，LIANG Jing-yuan，LIANG Guo-zhu，et al.Preliminary analysis on cone burning of solid propellant in end-burning rocket motors［J］.Chinese Journal of Explosives and Propellants，2006，29（5）：32-34.

［4］周長省，鞠玉濤，朱福亞.火箭彈設計理論［M］.北京：北京理工大學出版社，2005.

［5］董師顏，張兆良.固體火箭發動機原理［M］.北京：北京理工大學出版社，1996.

［6］邢耀國，董可海，沈偉.固體火箭發動機使用工程［M］.北京：國防工業出版社，2010.