改進型變步長光伏最大功率點快速跟蹤

王義飛， 吳 偉， 張皞華， 徐 悅

(上海大學理學院，上海200444)

針對21世紀的能源需求問題，光伏發電具有非常廣闊的發展前景，因為作為光伏發電動力的太陽光能可以說是取之不盡、用之不竭，而且清潔無污染.目前，光伏發電的研究重點主要集中在兩方面：一是尋找轉換效率高、成本低、來源豐富的光電轉換材料，以及對于新的更高轉換效率的電池結構的設計;二是在已有的電池轉換效率的基礎上提高電池的輸出效率.

對于一些內阻不變的供電系統，可以采用外加負載的阻值等于內阻的簡單方法獲得最大輸出功率.但在太陽能電池供電系統中，太陽能電池的輸出特性由于受到光照強度以及電池溫度的影響而不斷變化，呈現明顯的非線性，從而不可能使用上述的簡單方法來獲得最大輸出功率.為了實現光伏發電系統的功率輸出最大化，需要對光伏電池的輸出最大功率點進行跟蹤.由于在當前的技術條件下，太陽能光伏電池的轉換效率普遍偏低，加上原材料以及工藝的原因，使得光伏電池成本比其他方式的發電成本高很多.為了更好地推廣發展光伏電池，必須將已經獲得的能量最大限度地加以利用，因而最大功率跟蹤顯得十分必要.

近年來，人們對最大功率跟蹤技術進行了深人研究，已得到了多種算法［1］，如恒定電壓控制法、擾動觀測(perturbation and observation，P＆O)法、導納增量法、模糊控制法等.擾動觀察法和導納增量法是目前比較常用的自尋優方法［2］，即系統不用直接檢測光照強度和溫度，而是根據光伏陣列本身的電壓電流值確定最大功率點.

擾動觀察法算法簡單，容易實現，但缺點是達到最大功率點后擾動不會停止，而是在最大功率點處來回振蕩，造成能量損耗，而且擾動的步長越大，電壓振蕩越厲害［3］.如果在最大功率點處使用小步長可使振幅減小，但是過小的步長會引起跟蹤時間變長，影響跟蹤速度.因此，跟蹤步長的選取與能否很好地實現功率跟蹤關系密切.

本研究基于擾動觀察法提出一種改進的最大功率點跟蹤(maximum power point tracking，MPPT)方法，即基于功率斜率曲線的判斷標準，采用變步長的擾動觀察法進行MPPT控制，通過Matlab/Simulink仿真.結果表明，該方法具有跟蹤速度快、穩定性好、跟蹤精度高的特點.

1 光伏電池數學模型

1.1 模型的選取

本研究以目前應用最廣泛的晶體硅太陽能電池為模型進行模擬仿真.在常用的光伏電池模型基礎上，根據電池廠商提供的標準測試條件(T=25℃，G=1 000 W/m2)下的參數，包括短路電流Isc、開路電壓Voc、最佳工作電壓Vm、最佳工作電流Im、短路電流溫度系數αIsc以及開路電壓溫度系數βVoc等.De Soto等［4］提出了一種修正后的五參數電池模型，即

與標準情況相比，其他條件下的修正參數為

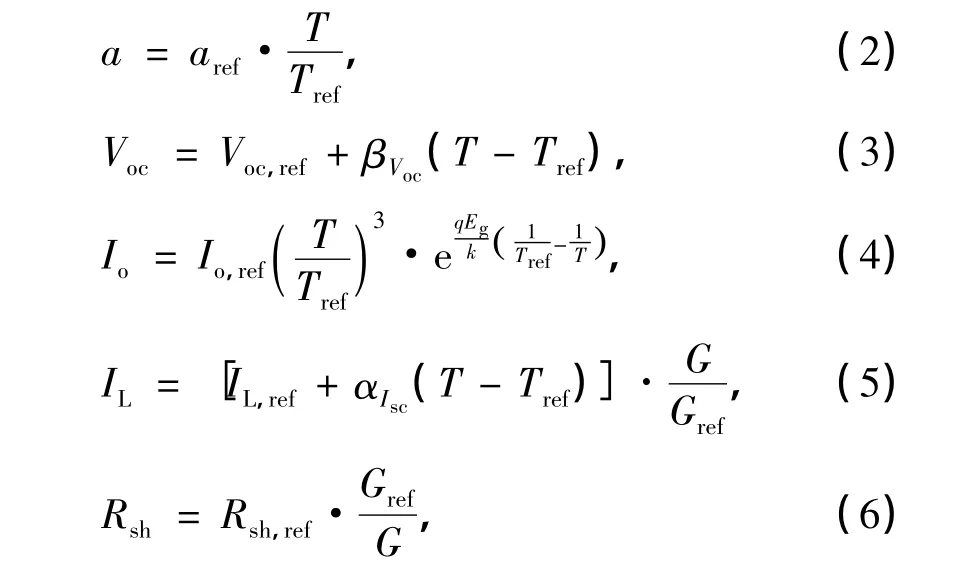
式中，ref表示電池廠商提供的標準測試條件，aref，Voc，ref，Io，ref，IL，ref，Rs，Rsh，ref均可以通過電池廠商所給的參數計算得到.本模型將Rs作為常數處理［4］，在Matlab/Simulink下得到的光伏模塊模型如圖1所示.

圖1 光伏電池的Simulink模型Fig.1 Model of a photovoltaic module in Simulink

1.2 輸出特性曲線仿真結果

采用上述模型建立 Matlab/Simulink模塊圖［5-7］，對不同光強度(1 200，1 000，800 W/m2)下的電池片進行模擬，得到輸出特性曲線.選用25 W光伏電池組件，參數為Vm=17.5 V，Im=1.43 A，Voc= 21.5 V，Isc=1.61 A.溫度選擇T=25℃.不同光照強度下的I-V和P-V特性曲線分別如圖2和圖3所示.

圖2 相同溫度(25℃)不同光強下的I-V特性曲線Fig.2 I-V curve of a photovoltaic model for different insolation level at the constant temperature(25℃)

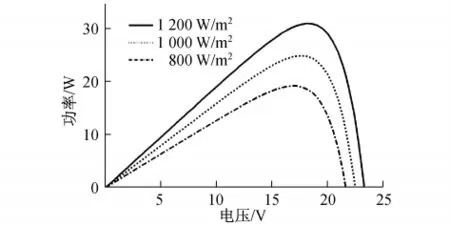
圖3 相同溫度(25℃)不同光強下的P-V特性曲線Fig.3 P-V curve of a photovoltaic module for different insolation levelatthe constanttemperature (25℃)

可以看出，在溫度(25℃)一定的條件下，隨著太陽光照強度的增加，光伏電池的短路電流明顯增大，而開路電壓會少量增大，最大輸出功率增大.

在光照強度一定(1 000 W/m2)的條件下，溫度為60，40，20℃時的I-V特性曲線和P-V特性曲線分別如圖4和圖5所示.

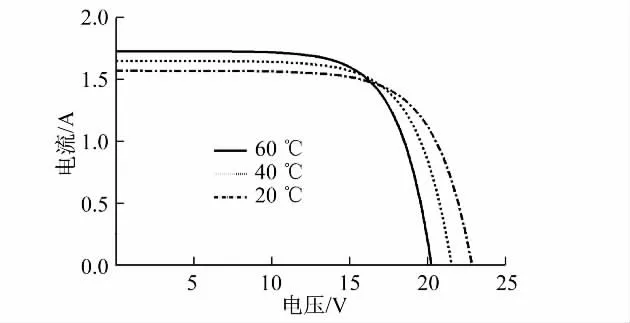
圖4 光強(1 000 W/m2)一定，不同溫度下的I-V曲線Fig.4 I-V characteristics of a photovoltaic module for different temperature level at the constant solar insolation(1 000 W/m2)

圖5 光強(1 000 W/m2)一定，不同溫度下的P-V曲線Fig.5 P-V characteristics of a photovoltaic module for different temperature levels at the constant solar insolation(1 000 W/m2)

由圖4和圖5可知，在太陽光照強度一定時，電池的開路電壓隨溫度的升高明顯下降，短路電流會有少量增加，最大輸出功率點明顯向右平移.

2 基于擾動觀察法的MPPT仿真

擾動觀察法是一種基于功率比較的方法，也是目前被廣泛采用的一種自適應控制方法.其基本原理是在原有的輸出電壓上增加一個擾動，通過實時采樣電池的輸出電壓和電流，計算出瞬時功率，然后與上一采樣得到的功率進行比較，依據功率增減變化情況對光伏系統工作電壓進行調節.擾動觀察法的工作流程［8］如圖6所示.

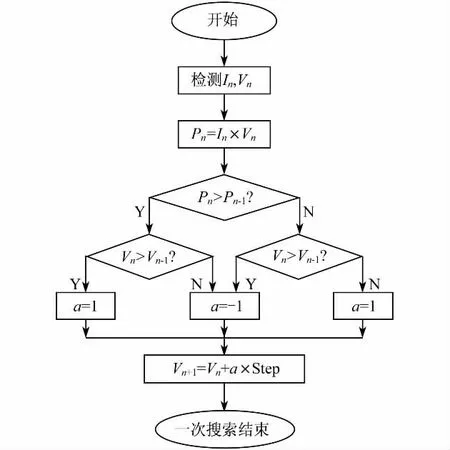
圖6 擾動觀察法流程圖Fig.6 Flowchart of P＆O control method

擾動觀察法類似冒泡法，通過周期性重復搜索調節，直至在最大功率點(maximum power point，MPP)附近振蕩.振蕩幅度的大小可以通過改變擾動步長的大小來調節，但是步長過小會使跟蹤的效率變低［3］.對于傳統的擾動觀察法，其擾動步長一般為固定大小.

本研究利用前述太陽能電池數學模型，在Matlab/Simulink環境下建立MPPT控制模塊，對傳統的擾動法進行計算機仿真，時間間隔為0.001 s.如果固定擾動步長為0.10 V，需要經歷0.18 s才能跟蹤到最大功率點，并在24.3～25.0 W范圍內不斷振蕩;如果步長減小為0.05 V，則需經歷0.35 s才可以跟蹤到最大功率點，并且在24.8～25.0 W范圍內不斷振蕩，結果如圖7所示.通過分析可以發現，步長越短，跟蹤時間越長，但振蕩范圍越小.

圖7 2種步長的擾動觀察法比較Fig.7 Comparison of two P＆O methods in different perturbation step size

通過分析傳統的固定步長的擾動觀察法存在的缺點，本研究提出一種變步長尋優的方法.目標是在離最大功率點比較遠的地方，可以使用大步長跟蹤，使跟蹤速度提高;在離最大功率點較近的地方，可以使用小步長跟蹤，使振蕩幅度減小.

通過分析光伏電池的P-V曲線可以發現，在距離最大功率點較遠的地方，斜率較大;在離最大功率點較近的地方，斜率逐漸減小，MPP處為0.圖8所示為標準測試條件下光伏電池的P-V和dP-V曲線，可以看出，在電壓0～15 V之間，dP-V曲線近似固定值.

圖8 標準測試條件下光伏電池的P-V和dP-V曲線Fig.8 P-V curve and dP-V curve for a photovoltaic module in standard test conditions

基于改進的變步長擾動法，得到 Matlab/ Simulink控制模塊如圖9所示，仿真得到的功率隨時間的變化曲線如圖10所示.可以發現，只需經歷0.12 s，就可跟蹤到輸出最大功率點，而且穩定在25 W處，幾乎沒有振蕩.與傳統的擾動觀察法比較，所用時間短、精度高.

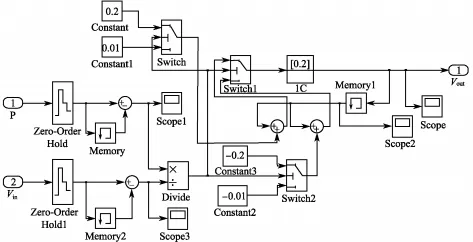
圖9 變步長擾動觀察法最大功率點跟蹤Simulink仿真模塊圖Fig.9 P＆O control method model of a photovoltaic module in Simulink

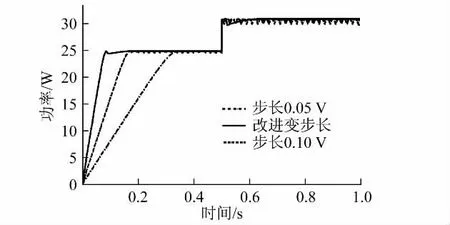
圖10 改進變步長法與傳統的擾動觀察法比較Fig.10 Comparison betweenproposedmethodand traditional P＆O method

因此，與傳統的擾動觀察法相比較，改進的擾動觀察法更具優越性，即最大功率點的跟蹤速度快，穩定性好.

3 結束語

本研究利用Matlab/Simulink建立光伏電池組件的計算機仿真模型，給出了隨光強和溫度變化下的輸出特性曲線.通過對傳統的擾動觀察法進行改進，提出一種基于功率斜率曲線的判斷標準，給出了改進擾動觀察法的Matlab/Simulink最大功率點跟蹤控制模型.仿真結果表明，該方法能夠適應光強和溫度的快速變化，最大功率點跟蹤速度快、穩定性好，能夠比傳統的擾動觀察法更好地滿足跟蹤時間和跟蹤精度的要求.

［1］ ESRAMT，CHAPMANP L.Comparison of photovoltaic array maximum power point tracking techniques［J］.IEEE Transaction on Energy Conversion，2007，22(2)：439-449.

［2］ 馮垛生.太陽光能發電原理與應用［M］.北京：人民郵電出版社，2007：95-132.

［3］ XIAOW D，DUNFORDW G.A modified adaptive hill climbing MPPT method for photovoltaic power system［C］∥35th Annual IEEE Power Electronics Specialists Conference.2004：1957-1963.

［4］ DESOTOW，KLEINS A，BECKMANW A，et al. Improvement and validation of a model for photovotaic array performance［J］.Solar Energy，2006，80：77-78.

［5］ 李煒，朱新堅.光伏系統最大功率點跟蹤控制仿真模型［J］.計算機仿真，2006，23(6)：239-243.

［6］ 茆美琴，余世杰，蘇建徽.帶有MPPT功能的光伏陣列MatLab通用仿真模型［J］.系統仿真學報，2005，17 (5)：1248-1251.

［7］ ROPPM E，GONZALEZS.Development of a MATLAB/ Simulink model of a single-phase grid-connected photovoltaic system［J］.IEEE Transactions on Energy Conversion，2009，24(1)：195-202.

［8］ 陳興峰，曹志峰，許洪華，等.光伏發電的最大功率點跟蹤算法研究［J］.可再生能源，2005(1)：8-11.