結構方程模型等同性檢驗及其在分組比較中的應用*

山西醫科大學(030001) 武淑琴 張巖波

結構方程模型等同性檢驗及其在分組比較中的應用*

山西醫科大學(030001) 武淑琴 張巖波△

目的通過探討結構方程模型等同性檢驗方法在分組比較中的應用，說明等同性檢驗的必要性和重要性。方法 結合抑郁癥病例-對照臨床研究中特質應對方式量表數據，利用LISREL軟件實現各種等同性檢驗及參數估計。結果 通過等同性考察，證實TCSQ量表在病例-對照研究中具有等同性。結論 對量表測量數據在進行分組比較時，首先須進行各種等同性檢驗，并在此基礎上，進一步進行潛變量均值結構的分析，在此前提下研究結果更可靠。

結構方程模型 等同性 分組比較 潛變量均值

*：國家自然科學基金資助(30972553);山西省自然科學基金資助(2010011051-2)

△通訊作者：張巖波

隨著結構方程模型(structure equation modeling，SEM)技術的廣泛應用，使得測量理論得以對于復雜的因素構建進行證實性的研究。在跨文化研究、分組比較均值結構(means structure)或多樣本比較等應用中，即使一個測量被證明有良好的信度與效度，也不能說明這些測量與其所測得的潛在因素在不同的受試對象上具有相同的意義。因此，須事先進行測量等同性(measurement invariance)檢驗，提供研究者因素構建、因子載荷、誤差估計在不同樣本間的等同或歧義性。所謂等同性是指同一測量施于不同的對象或在不同時點上使用時，測量分數應具有一定的恒定性，即當研究者利用一組測量題目測得一個心理概念并應用于組間比較，研究者必須假設項目分數與尺度對不同的受試對象(如不同性別、職業等)具有相同的意義。在實際工作中研究者卻往往忽略等同性的考察，本文以均值結構模型(means structure model)的分組比較為例，探討等同性檢驗的分析理論與方法。

原理與方法

1.均值結構模型

結構方程模型的一般表達形式(即均值結構模型)如下：

其中y是由p個內生指標組成的p×1向量，η是由m個內生潛變量組成的m×1向量，Λy是y在η上的p×m因子載荷矩陣，ε是p個測量誤差組成的p×1向量，τy是p×1向量(y的測量方程常數項)，x是由q個外源指標組成的q×1向量，ξ是由n個外源潛變量組成的n×1向量，Λx是x在ξ上的q×n因子載荷矩陣，δ是q個測量誤差組成的q×1向量，τx是q×1向量(x的測量方程常數項)，B是m×m系數矩陣，Γ是m×n系數矩陣，ζ是m×1殘差向量，α是m×1向量(結構方程的常數項)。模型假設誤差項ε、δ的均值為零;結構方程殘差項ζ的均值為零;誤差項ε、δ與因子η、ξ之間不相關，ε和δ不相關;殘差項ζ和 ξ、ε、δ之間不相關。

在式(1)中，如果 τy、τx、α 為0，則為中心化模型。

2.結構方程模型多組比較與等同性檢驗

根據結構方程模型分為中心化模型和均值結構模型，結構方程模型可進行相應的多組比較：(1)中心化模型多組比較需要進行第一階段分析，即檢驗各樣本組是否有相同的結構模式。包括確定基準模型(baselinemodel)，因子載荷、因子方差、誤差方差、因子協方差等的等同檢驗;(2)均值結構模型多組比較首先要進行第一階段分析，在確定了基準模型及各組具有相同結構模式的基礎上，再進行第二階段分析，即檢驗各組均值或截距是否有統計學意義。

(1)第一階段分析

①確定基準模型

首先要了解模型的形式在各組是否相同，包括：因子個數(如在實例分析中病例與對照組中都是2個因子)，題目與因子的從屬樣式。形式相同是指用同一個模型擬合不同的組時總的擬合指數良好，其說明每個組都可以用同一模型去描述，該模型被稱為基準模型。

Bollen提出：如果兩個模型具有相同的參數矩陣，維度相同，固定參數、自由參數、約束參數的位置相同，則定義兩個模型具有相同形式〔1〕。在結構方程模型中，形式相同從實際意義上還意味著因子載荷、因子方差以及誤差方差的參數是自由或固定，在所有的組中是一致的(但參數估計值不一定相等)〔2〕。

②因子載荷等同檢驗

假定模型形式相同的檢驗可以通過，就可以進行多組因子載荷等同性檢驗(metric invariance/factor loading invariance)。例如病例組中積極應對因子在條目TCSQ3的載荷與對照組中積極應對因子在條目TCSQ3的載荷相等，即兩組的因子載荷等同(Λg1=Λg2)。

③因子方差等同檢驗

因子方差等同(factor variance invariant)即Φg1，jj= Φg2，jj，是檢驗不同組別對應因子 η、ξ的方差是否相同。

④誤差方差等同檢驗

誤差方差等同(indicator uniqueness variance invariant)即Θg1=Θg2，是當因子方差等同時關于Θg1=Θg2的檢驗。

⑤因子協方差等同檢驗

因子協方差等同(factor covariance invariance)即Φg1=Φg2，是檢驗不同組別對應的因子協方差是否相同。若與因子方差等同檢驗一起進行，相當于比較各組的因子相關系數。

對上面提出的各種等同性檢驗，可以根據Bollen提出的逐步增加限定條件的辦法進行等同性檢驗。增加等同限制后，模型的卡方值和自由度都將會發生改變。增加等同限制后得到的模型與原模型屬于嵌套模型，模型擬合檢驗采用通常的模型比較原理：若Δχ2(自由度為Δdf)有統計學意義，說明卡方改變了很大，意味著增加等同限制后，擬合指數變差，各組共享同一個等同限制的模型不可行;反之，若 Δχ2(自由度為Δdf)無統計學意義，說明卡方改變不大，意味著增加等同限制后，擬合指數變化不太大，可以接受各組等同的假設。

(2)第二階段分析

①指標截距等同檢驗

在進行完第一階段各種檢驗后，接著可以進行指標截距是否相同的檢驗(indicator intercept invariant)，即檢驗 τg1= τg2。

②因子均值等同檢驗

因子均值等同是對各組因子均值是否相同的檢驗，即檢驗 κg1=κg2。

檢驗各組對應因子均值是否相同，是均值結構方程模型主要研究的內容，也是在實際應用時主要分析的結果。如果第一階段各種等同性(主要指因子載荷等同)檢驗步驟不能通過，將會使各組因子失去可比性，因而不能進行各組因子均值的檢驗。對于均值結構模型多組比較，在進行研究時，首先要做第一階段分析的檢驗，然后研究者可以根據研究的問題，對所檢驗的項目進行自由組合。實際應用時，第一階段分析的檢驗并不是全部都要進行，只要在確定基準模型后通過了因子載荷等同檢驗，就可以進行問題的研究。

在進行多組比較時，如果整體上拒絕了原假設，說明組間均值差異有統計學意義，接下來可以進行多重比較，即比較每兩組間因子均值差異，這與傳統的方差分析相類似。因子均值多重比較也屬于這類事后(post hoc)比較，其方法與方差分析的事后比較一樣，需要調整檢驗水準來控制I型錯誤〔2-4〕。

實例分析

為了說明結構方程模型等同性在多組比較中的應用，采用2008年某醫院關于抑郁癥臨床研究中特質應對方式問卷(TCSQ)調查量表數據資料進行分析。TCSQ包括構念消極應對(NC)、積極應對(PC)2個維度和20個條目(TCSQ1～TCSQ20，見表1)。對病人和正常人采用病例-對照進行分組比較，調查對象共801例，其中病例組395例，對照組406例。將調查資料檢查、核實后用ACCESS建立數據庫，對量表的個別條目進行處理，利用SPSS13.0對TCSQ問卷存在的缺失數據進行缺失值估計。

由量表結構可以建立如下的均值結構方程：

式中i指NC各條目，g=0、1表示對照組、病例組，ξ1表示潛變量消極應對(NC)。

式中j指PC各條目，g=0、1表示對照組、病例組，ξ2表示潛變量積極應對(PC)。

首先利用LISREL 8.53編寫程序進行第一階段各種等同性的分析。包括確定基準模型，因子載荷等同、因子方差/協方差等同、誤差方差等同等一系列檢驗，各分析模型的擬合指數見表2〔5-7〕。

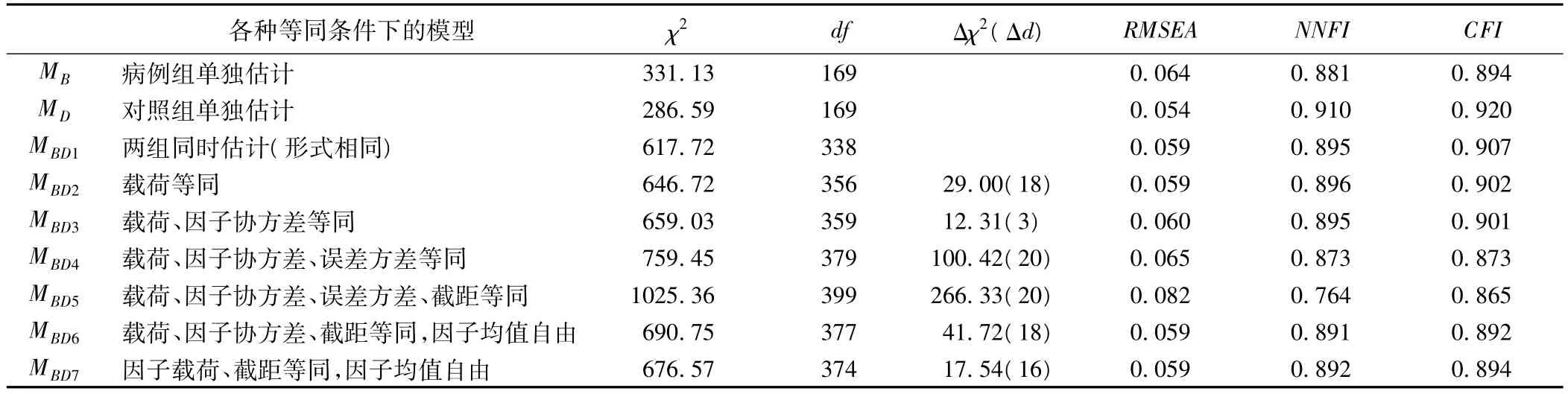
表2 病例-對照組測量模型各模型的擬合指數

在增加限制的時候，通常情況下是整套因子載荷、方差/協方差或其他等同同時限制為相同。如果發現模型擬合優度變差時，就要設法找到那些導致模型擬合變壞嚴重的參數，從而掌握各組產生差異的原因。

接著進行第二階段等同性檢驗，首先進行兩組因子載荷、因子協方差、截距等同的限制(見表2MBD6)，擬合情況十分理想。最后進行因子載荷、截距等同、因子均值自由的檢驗(見表2MBD7)，結果顯示擬合情況很好。

由LISREL程序結果顯示病例組的因子均值(KAPPA)消極應對(NC)、積極應對(PC)與對照組的因子均值差異有統計學意義，見表3。

表3 KAPPA(病例組)

由表3可知，病例組消極應對因子均值均低于正常對照組，積極應對因子均值高于正常對照組(P＜0.001)。

討 論

1.關于基準模型

模型的形式可能會因為以下原因而不同：(1)各組模型所含因子不同;(2)各組所含因子相同，但同一潛變量所屬層次會不一樣。以病例和對照兩組比較為例，假設MB是病例組擬合最佳模型，MD是對照組擬合最佳模型，而MT是研究者預先設定好的能符合病例和對照兩組的共同模型，MT的選擇要同時兼顧并盡量擬合兩組，所以用MT擬合病例組數據時比MB差;同理，用MT擬合對照組數據時也比MD差。但只要這種差別不大，就可以認為病例與對照兩組都可以用同一個模型去描述。

在多組比較的一系列模型檢驗當中，進行模型的形式相同檢驗是最基本的要求。如果MT對兩組已經擬合不好，再加上其他等同性限制(如兩組的因子載荷相同)，模型擬合會更差。再者，由于MT比MB和MD的擬合都差，所以如果MB或MD已經擬合不好的話，則不宜做進一步的多組比較。

2.部分等同模型的比較

增加因子載荷的等同性限制后，若模型的擬合指數變壞，有些學者認為不應該再進行其他等同的檢驗，對于組間均值差異也不應再進行比較。但是也有些學者會設法找到那些不相等的因子載荷，允許這些載荷在各組自由估計，進而用這些部分測量等同(partial metric invariance)的模型作進一步的多組比較。關于部分測量等同模型能否繼續做組間的均值差異比較，Vandenberg和Lance建議在下面的情況下才可以：(1)只允許極少數題目在兩組的載荷不相同;(2)要有充分的理論依據支持;(3)在不同樣本得出相同結果〔3〕。

3.等同性的統計學與實際意義

結構方程模型的等同性最大的特點是對測量工具(如問卷)在進行比較的各組中是否有可比性，即檢驗了測量工具在各組是否都適用，檢驗多組比較的結果是建立在相同的結構模型基礎上。從統計學上來說，與方差分析相比較，是對分組比較方法最大的進步。另外，從實際研究角度看，利用等同性找到了組間相同參數，使組間差異體現得更加精確與可靠。

總之，結構方程模型的多組比較除了調整測量誤差外，還克服了方差分析不能對測量工具進行等同性檢驗的缺點，使多組比較的分析結果更能充分體現客觀實際，結論更加合理。

1.廖福挺著，高勇譯.分組比較的統計分析.重慶大學出版社，2007：97-124.

2.侯杰泰，溫忠麟，成子娟.結構方程模型及應用.教育科學出版社，2004：80-104.

3.Vandenberg，Lance.A review and synthesis of the measurement invariance literature：Suggestions，practices，and recommendations for organizational research.Organizational Research Methods，2000，3(1)：4-70.

4.Vandenberg.Toward a further understanding of and improvement in measurement invariance methods and procedures.Organizational Research Methods，2002，5(2)：139-158.

5.J?reskog KG，S?rbom D.LISREL 8：User’s Reference Guide Scientific Software International，Inc.1999-2001.

6.Yu SC，Yu MN.Comparison of interent-based questionnaries in taiwan using multisample invariance approach.Cyber Psychology＆Behavior，2007，10(4).

7.Lau PWC，Cheung MWL，Ransdell LB.A structural equation model of the relationship between body perception and self-esteem：Global physical self-concept as themediator.Psychology of Sport and Exercise，2008，9：493-509.

Test of M easurement Invariance for Structure Equation M odel and its App lication in M ultip le Com parison Studies

WuShu-qin，ZhangYanbo．ShanxiMedicalUniversity(030001)，Taiyuan．

Objective To illustrate the necessity and importance ofmeasurement invariance test for structure equationmodel inmultiple comparison studies.MethodsTrait Coping Style Questionnaire(TCSQ)data in depression case-control study were analyzed and LISREL was used to test invariance and estimate parameter.ResultsMeasurement invariance test verified that TCSQ questionnaire had invariance in case and control group of depression data.ConclusionMeasurement invariance should be tested first，then analyzed latent mean structure in multi-group comparison for questionnaire data.The results were more reliable in this precondition.

Structure equation models;Invariance;Multiple comparison;Latentmeans