準一維無序體系電子局域化及輸運特性

宋招權，徐慧, 馬松山，劉小良

（中南大學 物理科學與技術學院，湖南 長沙，410083）

準一維無序體系電子局域化及輸運特性

宋招權，徐慧, 馬松山，劉小良

（中南大學 物理科學與技術學院，湖南 長沙，410083）

在單電子緊束縛近似下，利用多對角全隨機厄米矩陣算法，結合負本征值理論和無限階微擾理論及傳輸矩陣方法，研究準一維多鏈無序體系中電子波函數局域化特性及其電子輸運特性。研究結果表明：由于格點能量無序，準一維多鏈無序體系電子波函數呈現出局域化特性；格點能量無序度減小會導致在中間能區發生退局域化現象，表現為在中間能區電子波函數的局域長度大于體系格點數，即出現擴展態，且出現擴展態的能量區間隨著無序度的減小而增大的趨勢；同時，隨著鏈數的增加，體系有向退局域化方向發展的趨勢；在中間能區電子輸運透射系數較大，而在低能區及高能區透射系數較小，同時，格點能量無序與維度效應對體系的電子輸運存在競爭效應，當體系格點數及鏈數一定時，體系的透射系數隨著格點能量無序度的增大而減小，而當體系格點數及格點能量無序度一定時，準一維多鏈無序體系的透射系數隨著體系鏈數的增大而增大。

準一維無序體系；電子局域化；電子輸運

近年來，隨著納米科技和分子電子學的發展，碳納米管、納米線及DNA分子導線等一維、準一維體系由于具有獨特的電學性能而具有廣闊的應用前景，如可用作納米電子器件的導線、構筑特殊的納電子元件（如場效應管、電子開關）及生物分子器件等，同時，由于在碳納米管、納米線及DNA分子導線等低維體系電子材料和器件的生產、制備過程中不可避免地會存在雜質態、缺陷等無序因素，而無序的引入會導致體系的電子波函數呈現局域化特性[1]，從而對其電子輸運特性產生影響；因此，對于一維、準一維等低維無序體系電子輸運性質的研究已成為國內外研究的熱點[2?6]。對于一維單鏈無序體系，其電子波函數是局域化的，電子只能通過熱激發，在不同局域態之間跳躍輸運，而對于準一維無序體系，在弱無序情況下，在能帶中心出現退局域化現象[7?8]；同時，由于現實的碳納米管、納米線及DNA分子導線等都有一定的寬度，準一維無序模型更能反映其真實特征。因此，很多研究者注重于準一維無序體系電學特性的研究。如Hjort等[9]利用傳輸矩陣方法研究了準一維聚乙烯、聚乙炔等無序體系的電子波函數局域化現象；徐慧等[10?12]利用五對角隨機厄米矩陣的求解方法，實現了對準一維無序體系的態密度及本征矢的數值計算；Gallos等[13]利用蒙特卡羅方法計算了準一維無序體系電子的平均遷移率對溫度的依賴性；Ivanov等[14]計算研究了準一維無序體系中具有很小能量差的幺正對稱態的局域態密度關聯函數。然而，人們對于準一維體系中電子波函數的局域化特性的研究，特別是維度效應對準一維無序體系電子波函數局域化及電子輸運的影響的研究很少。在此，本文作者通過構建準一維多鏈無序模型，在單電子緊束縛近似下，研究準一維多鏈無序體系中電子波函數局域化特性及其電子輸運特性。

1 模型與方法

對1個有k條平行鏈的準一維無序系統（見圖1），考慮到雖然次近鄰格點間的相互作用對體系電子結構會產生附加的影響，但其影響相對最近鄰格點間的相互作用來說小近1個數量級[15]，因此，為了使問題簡化，只計及最近鄰格點間跳躍積分，即對第i個格點僅考慮它與i?k，i?1，i+1和i+k格點間的相互作用時，體系的哈密頓量可表示為[16]：

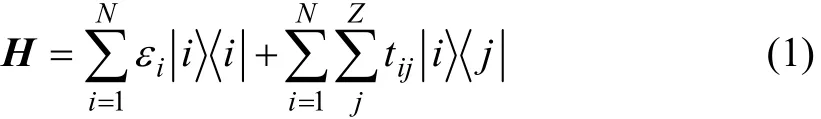
其中：N為體系的格點總數；Z為格點i最近鄰格點的數目；εi為第i格點的位能；tij為描述電子在i與j格點之間轉移的躍遷矩陣元。本研究只考慮對角無序，即εi取一組均勻分布在區間[?W/2,W/2]的隨機數，其中，W代表體系的格點能量無序度，非對角項tij取常數tij= ?1。

圖1 準一維多平行鏈無序模型Fig.1 Model of quasi-one-dimensional disordered system

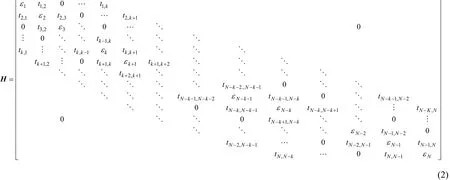
顯然，上述準一維多鏈無序體系的哈密頓量可表示為一多對角的對稱矩陣，即：

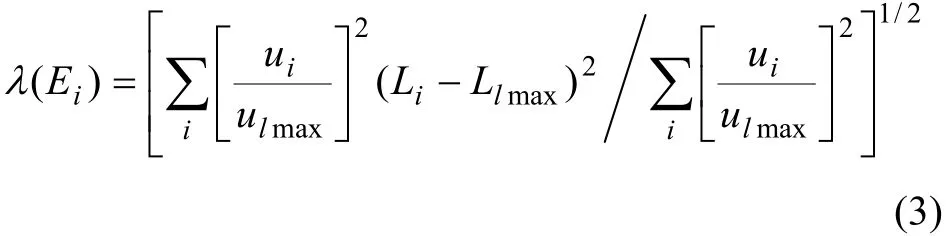
利用多對角全隨機厄米矩陣算法結合負本征值理論[17?18]和無限階微擾理論[19]很容易求解其能量本征值及本征矢。對于每一能量本征值，其對應的本征矢擴展范圍λ（Ei）可表述示為：其中：ulmax為本征矢分量最大值；Li和Llmax分別為各本征矢分量和分量最大值對應的格點。若電子波函數是局域化的，其擴展范圍通常稱為波函數的局域長度；因此，對應于能量本征值Ei電子波函數局域長度，可以通過數值計算得出。

同時，將體系重新編號。假定每條鏈所含原子個數都為l，且N=k×l，則沿鏈方向和垂直于鏈的方向建立坐標后，體系中每個格點原子的坐標可記為（m,n），其中，1≤m≤k，1≤n≤l。體系的電子波函數表示為格點軌道波函數的線性組合，體系的哈密頓量作用在波函數ψ上則可以將薛定諤方程Hψ=Eψ表示為：

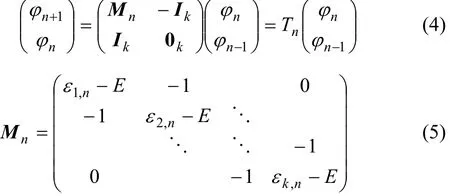
因此，在整個體系兩端波函數的幅值可以表示為：

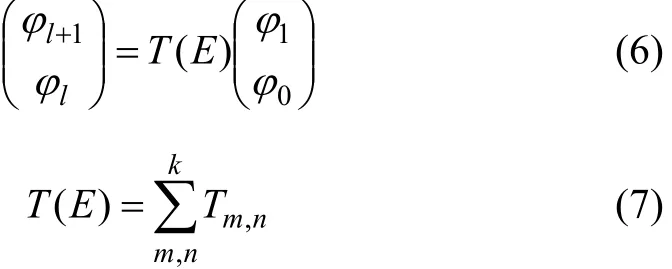
其中：T（E）為整個體系的總的透射系數[20?21]；Tm,n為進入第m條鏈的電子從第n條鏈透射出來的概率。

2 計算結果與分析

對于無序體系，當格點數達2×103時，其電子結構已趨向穩定，其電子波函數局域化特性及其局域態分布都具有很好的穩定性[22]，因此，選擇包含3×103個格點的準一維多鏈，計算其電子波函數局域化特性及其輸運特性。

2.1 電子波函數局域態

在準一維無序體系中，由于無序的存在，其電子波函數同樣呈現出局域化特性。計算了格點數量N= 3 000，且格點能量無序度W=1.0的準一維三鏈無序體系電子波函數，如圖2所示。從圖2可見：對于本征能量為Ei= ?0.993 39 eV的電子態，其電子波函數被局限在一個有限的范圍內，在其局域中心位置（格點857處）的電子波函數的分量最大，但隨著離局域中心位置距離的增大而迅速減小；因此，電子波函數分量的衰減快慢反映了其電子波函數的局域化程度，可以通過局域長度來描述。

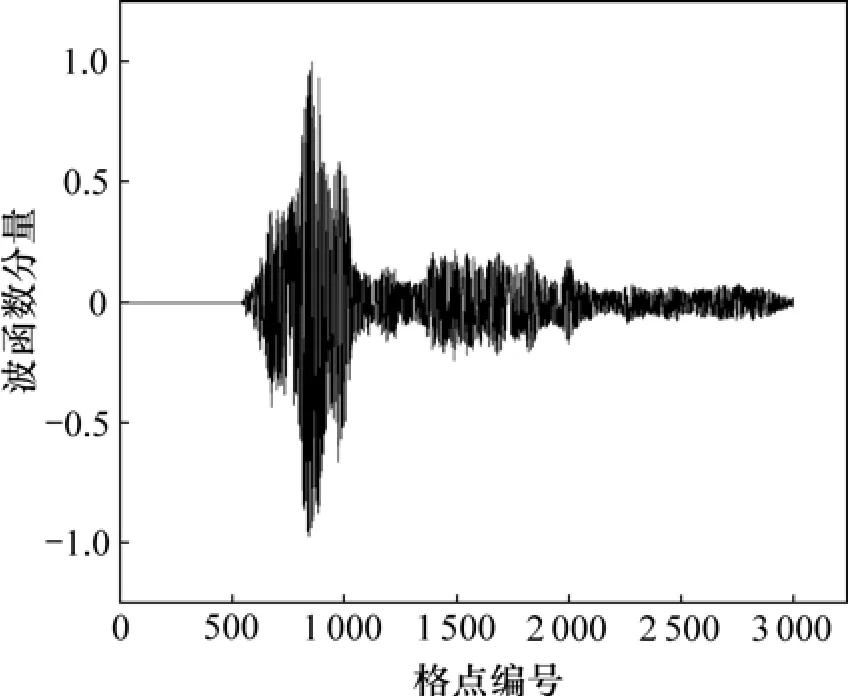
圖2 準一維多平行鏈電子波函數的局域化Fig.2 Electronic localization of quasi-one-dimensional disordered system

2.2 電子波函數局域長度

準一維多平行鏈無序體系電子局域長度與能量的關系如圖3所示。

由圖3（a）可知：當格點原子數及鏈數確定時，隨著格點能量無序度的減小，在能區中間電子波函數的局域化程度減弱，局域長度增大；當W＜2.0時，在能區中央開始出現電子波函數局域長度大于鏈長現象（對格點總數為N=3 000，鏈數為k=3體系，每條鏈所含原子個數為1 000），即出現了擴展態，并且隨著格點能量無序度的進一步減小，電子波函數擴展長度進一步擴大，出現擴展態的能量區間也呈增大的趨勢。由圖3（b）可知：在格點原子數及格點能量無序度一定時，當鏈數較小時（如圖中k＜3的情況），在整個能量范圍內電子波函數的局域長度均小于系統的格點數，電子波函數局域化程度比較強。而對于k=5的多鏈無序體系，在中間一定的能量區間內，存在著局域長度大于鏈長的擴展態。可見，隨著鏈數的增加，體系有向退局域化方向發展的趨勢。這是因為：在多鏈體系中，相鄰格點原子之間的交疊積分的數目增加，擴大了格點間短程關聯相互作用，而關聯的引入會導致體系出現退局域化現象[7?8]。雖然存在無序，體系電子波函數具有局域化的傾向，但當無序度一定時，隨著關聯引入，中間能區可以出現擴展態，體現了維度效應的影響。

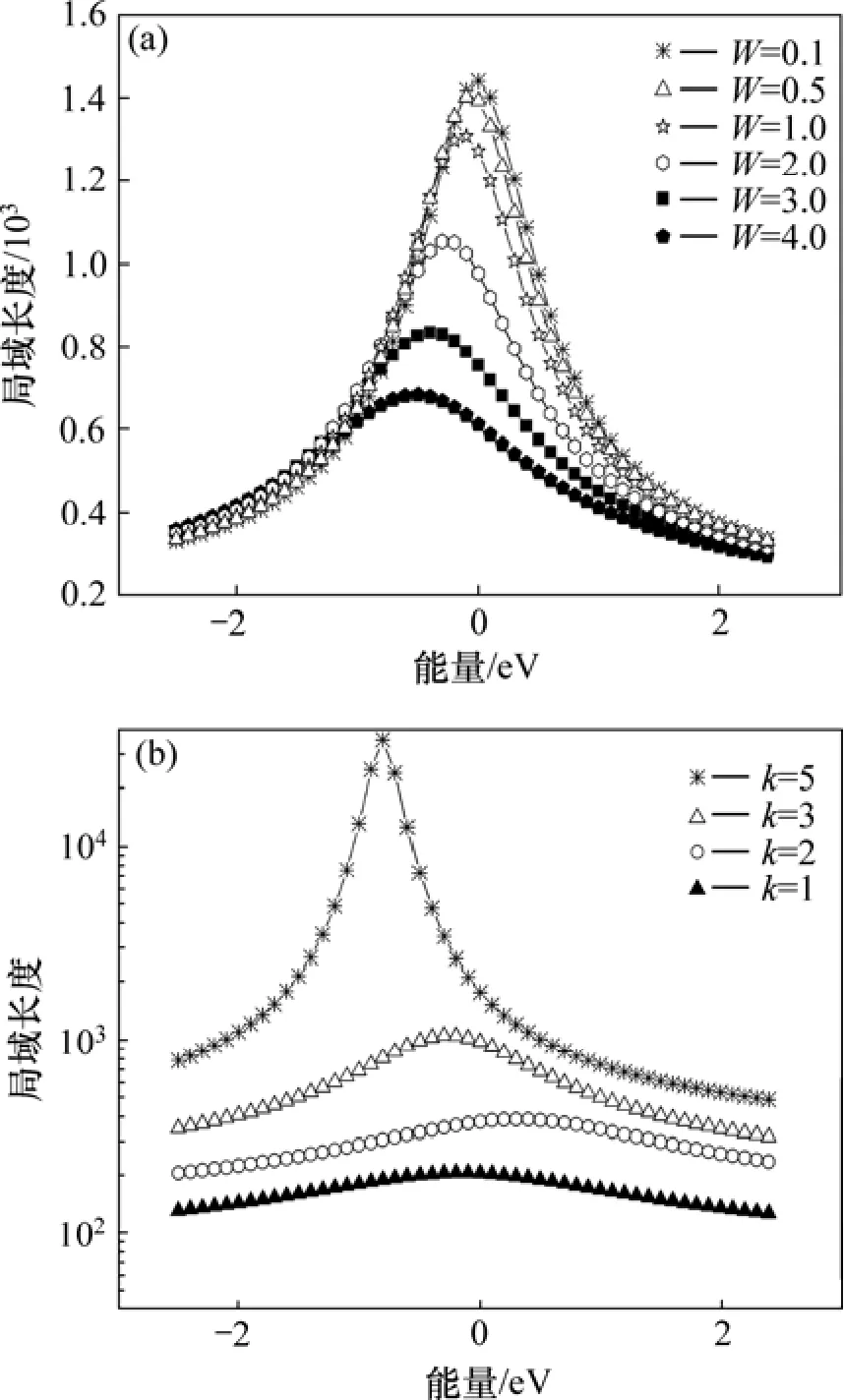
圖3 準一維無序體系的局域長度隨能量的變化Fig.3 Relationship between localization length and energy of quasi-one-dimensional system

2.3 準一維多鏈無序體系的電子輸運特性

準一維多平行鏈無序體系透射系數與能量的關系如圖4所示。

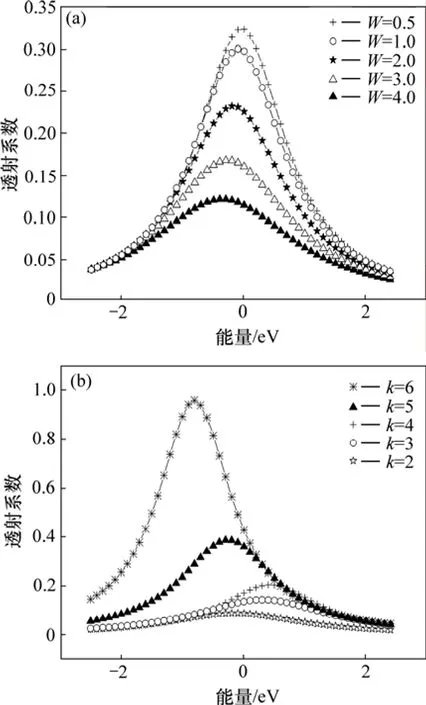
圖4 準一維無序體系的透射系數隨能量的變化Fig.4 Relationship between transmission coefficient and energy of quasi-one-dimensional system

由圖4可知，準一維多鏈無序體系的透射系數總體上都呈現出在中間能區透射系數較大，而在低能區及高能區透射系數較小的特性。這是因為在準一維多鏈無序體系的中間能區電子波函數局域化程度弱，電子波函數擴展范圍大，所以，電子輸運的透射系數也大。同時，由圖4（a）可知：當體系格點數及鏈數一定時，準一維多鏈無序體系的透射系數隨著格點能量無序度的增大而減小。正是由于存在無序，體系電子波函數呈現局域化的特性，無序度越大，電子波函數局域化程度越大；因此，隨著體系格點能量無序度的增大，體系電子輸運的透射系數減小。而由圖4（b）可知：當體系格點數及格點能量無序度一定時，準一維多鏈無序體系的透射系數隨著體系鏈數的增大而增大，同樣體現了維度效應的影響。一方面，隨著體系鏈數的增加，體系電子波函數發生退局域化現象，其局域化程度降低，擴展范圍增大；另一方面，隨著體系鏈數的增加，體系電子輸運的通道增加，同時，在格點數一定的情況下，鏈數越多，每條鏈上的格點原子數目越小，電子透射的距離越短，所以，體系電子輸運透射系數隨著鏈數的增大而增大。可見，在準一維無序體系，格點能量無序與維度效應對體系的電子輸運存在競爭特性。

3 結論

（1） 準一維多鏈無序體系中由于格點能量無序的存在，其電子波函數同樣呈現出局域化特性。

（2） 當體系格點數及鏈數確定時，格點能量無序度的減小會導致在中間能區發生退局域化現象，表現為在中間能區電子波函數的局域長度大于體系格點數，即出現擴展態，且出現擴展態的能量區間隨著無序度的減小而呈增大的趨勢；同時，隨著鏈數的增加，體系有向退局域化方向發展的趨勢。

（3） 準一維多鏈無序體系的透射系數在中間能區較大，而在低能區及高能區透射系數較小；同時，格點能量無序與維度效應對體系的電子輸運存在競爭效應，當體系格點數及鏈數一定時，準一維多鏈無序體系的透射系數隨著格點能量無序度的增大而減小，當體系格點數及格點能量無序度一定時，準一維多鏈無序體系的透射系數隨著體系鏈數的增大而增大。

[1] Anderson P W. Absence of diffusion in certain Random lattices[J]. Phys Rev, 1958, 109（5）： 1492?1505.

[2] Rodin A S, Fogler M M. Numerical studies of variable-range hopping in one-dimensional systems[J]. Phys Rev B, 2009, 80（15）： 155435?12.

[3] Maul R, Wenzel W. Influence of structural disorder and large-scale geometric fluctuations on the coherent transport of metallic junctions and molecular wires[J]. Phys Rev B, 2009, 80（4）： 045424?11.

[4] HU Dong-sheng, LU Xiu-juan, ZHANG Yong-mei, et al. Transport properties of a random binary side-coupled chain[J]. Chin Phys B, 2009, 18（6）： 2498?2501.

[5] Bascones E, Estévez V, Trinidad J A, et al. Electronic correlations and disorder in transport through one-dimensional nanoparticle arrays[J]. Phys Rev B, 2008, 77（24）： 245422?24.

[6] Ben-Naim E, Krapivsky P L. Strong mobility in weakly disordered systems[J]. Phys Rev Lett, 2009, 102（19）： 190602?4.

[7] Brower P W, Mudry C, Simons B D, et al. Delocalization in coupled one-dimensional chains[J]. Phys Rev Lett, 1998, 81（4）： 862?865.

[8] Sedrakyan T, Alexander O. Localization-delocalization transition in the quasi-one-dimensional ladder chain with correlated disorder[J]. Phys Rev B, 2004, 70（21）： 214206?9.

[9] Hjort M, Stafstrom S. Localization in quasi-one-dimensional systems[J]. Phys Rev B, 2000, 62： 5245?5250.

[10] 徐慧. 準一維無序系統的電子結構[J]. 計算物理, 1997, 14（4）： 574?576.

XU Hui. Electronic structure of quasi-one-dimensional disordered systems[J]. Chin J Comp Phys, 1997, 14（4）： 574?576.

[11] 宋招權, 徐慧, 李燕峰, 等. 非對角無序和維數效應對低維無序系統電子結構的影響[J]. 物理學報, 2005, 54（5）： 2198?2201.

SONG Zhao-quan, XU Hui, LI Yan-feng, et al. The effects of non-diagonal disorder and dimensions in low-dimensional disordered electronic system[J]. Acta Phys Sin, 2005, 54（5）： 2198?2201.

[12] 劉小良, 徐慧, 馬松山, 等. 準二維無序系統的電子結構[J].物理學報, 2006, 55（5）： 2492?2497.

LIU Xiao-liang, XU Hui, MA Song-shan, et al. The electronic structure of quasi-two-dimensional disordered systems[J]. Acta Phys Sin, 2006, 55（5）： 2492?2497.

[13] Gallos L K, Movaghar B, Siebbeles L D A. Temperature dependence of the charge carrier mobility in gated quasi-onedimensional systems[J]. Phys Rev B, 2003, 67（16）： 165417?8.

[14] Ivanov D A, Ostrovsky P M, Skvortsov M A. Correlations of the local density of states in quasi-one-dimensional wires[J]. Phys Rev B, 2009, 79（20）： 205108?15.

[15] Kiwi M, Ramirez R, Trias A. Effects of overlap and nextnearest-neighbor interactions in tight-binding calculations[J]. Phys Rev B, 1978, 17（8）： 3063?3069.

[16] Carpena P, Bemaola-Galvan P, Ivanov P C, et al. Metal-insulator transition in chains with correlated disorder[J]. Nature, 2002, 418： 955?959.

[17] Dean P. Vibrational spectra of diatomic chains[J]. Proc Roy Soc, 1960, 254： 507?521.

[18] Dean P. The vibrational properties of disordered systems： Numerical studies[J] Rev Mod Phys, 1972, 44（2）： 127?168.

[19] WU Shi-yu, ZHENG Zhao-bo. Amplitude analysis of localization in one-dimensional disordered systems. Vibrational states of an isotopically disordered binary chain[J]. Phys Rev B, 1981, 24（8）： 4787?4795.

[20] Buttiker M, Imry Y, Landauer R, et al. Generlized many channel conductance formula with application to small rings[J]. Phys Rev B, 1985, 31（10）： 6207?6215.

[21] GUO Ai-min, XIONG Shi-jie. Effects of contact and efficient charge transport in G4-DNA molecules[J]. Phys Rev B, 2009, 80（3）： 035115?5.

[22] 徐慧, 曾紅濤. 無序系統中電子局域態分布[J]. 物理學報, 1992, 41（10）： 1666?1671.

XU Hui, ZENG Hong-tao. Distribution of electronic localization in the disordered system[J]. Acta Phys. Sin., 1992, 41（10）： 1666?1671.

（編輯 趙俊）

Characteristics of electronic localization and transportation in quasi-one-dimensional disordered systems

SONG Zhao-quan, XU Hui, MA Song-shan, LIU Xiao-liang
（School of Physical Science and Technology, Central South University, Changsha 410083, China）

Based on a tight-binding disordered model describing a single electron band, a model of quasi-onedimensional disordered systems with several chains was established using the negative eignvalue theory, infinite order perturbation theory and transfer matrix method. The characteristics of electronic localization and transportation in quasi-one-dimensional disordered systems with several chains were discussed. The results indicate that the electronic states of the quasi-one-dimensional disordered systems are localized due to energy disorder of the lattices. The localization length increases with the decrease of the strength of energy disorder of the lattices. At the energy band center, there exist some extent states whose localization lengths are lager than that of the atoms of the chains in weak disorder. Meanwhile, with the increase of the number of the chains, the delocalization can be found. In addition, the transmission coefficient of electron transportion in quasi-one-dimensional disordered system is much higher in the energy band center than that in high and low energy region, and decreases with the increase of the energy disorder degree of the lattices, but increases with the increase of the number of the chains.

quasi-one-dimensional disordered systems; electronic localization; electronic transportation

O482.4，TB303

A

1672?7207（2011）01?0125?05

2009?09?16；

2010?12?27

高等學校博士點專項科研基金資助項目（20070533075）；湖南省科技計劃項目（2009FJ3004）

徐慧（1958?），男，湖南常德人，博士，教授，從事材料性能計算模擬研究；電話：13907488179；E-mail： xuhui@mail.csu.edu.cn