任意復(fù)雜薄壁截面自由扭轉(zhuǎn)常數(shù)的數(shù)值計(jì)算方法

康瀾，張其林，王忠全，吳杰

（1. 同濟(jì)大學(xué) 土木工程學(xué)院，上海，200092；2. 中交四航工程研究院有限公司，廣東 廣州，510230）

任意復(fù)雜薄壁截面自由扭轉(zhuǎn)常數(shù)的數(shù)值計(jì)算方法

康瀾1,2，張其林1，王忠全1，吳杰1

（1. 同濟(jì)大學(xué) 土木工程學(xué)院，上海，200092；2. 中交四航工程研究院有限公司，廣東 廣州，510230）

針對(duì)任意復(fù)雜薄壁截面自由扭轉(zhuǎn)常數(shù)的計(jì)算，提出一種便于計(jì)算機(jī)實(shí)現(xiàn)的建模方式和計(jì)算方法。采用一系列具有寬度的線(xiàn)段模擬薄壁截面，根據(jù)薄壁截面剪力流計(jì)算理論，編寫(xiě)相應(yīng)計(jì)算程序，計(jì)算得到任意復(fù)雜薄壁截面的自由扭轉(zhuǎn)常數(shù)。把本文的計(jì)算理論和計(jì)算方法運(yùn)用到大型斜拉橋蘇通大橋的截面計(jì)算中，并與Midas計(jì)算結(jié)果進(jìn)行比較。計(jì)算結(jié)果表明：本文的建模方式實(shí)現(xiàn)了與CAD的無(wú)縫連接，方便工程應(yīng)用；本文的計(jì)算方法對(duì)于不同剪力流指定方式得到相同的計(jì)算結(jié)果，克服了Midas的計(jì)算缺陷，驗(yàn)證了本文計(jì)算方法的正確性和穩(wěn)定性。

橋梁工程；薄壁截面；自由扭轉(zhuǎn)常數(shù)；數(shù)值計(jì)算方法；剪力流

薄壁構(gòu)件由于加勁肋的存在，斷面形式越來(lái)越復(fù)雜，增加了截面特性的計(jì)算難度，尤其是其抗扭常數(shù)的計(jì)算。任意開(kāi)閉口薄壁截面的抗扭常數(shù)可分為自由扭轉(zhuǎn)常數(shù)和翹曲扭轉(zhuǎn)常數(shù)。對(duì)于開(kāi)口薄壁截面，它的翹曲扭轉(zhuǎn)常數(shù)要遠(yuǎn)遠(yuǎn)大于自由扭轉(zhuǎn)常數(shù)；而對(duì)于閉口截面，它的自由扭轉(zhuǎn)常數(shù)對(duì)扭轉(zhuǎn)剛度的貢獻(xiàn)也不可忽略。因此，如何準(zhǔn)確計(jì)算自由扭轉(zhuǎn)常數(shù)對(duì)于薄壁截面特別是閉口為主的薄壁截面非常重要[1?2]。許多學(xué)者對(duì)自由扭轉(zhuǎn)常數(shù)的數(shù)值計(jì)算理論和方法進(jìn)行了大量研究工作[3?4]。杜柏松等[5]通過(guò)自由扭轉(zhuǎn)理論推導(dǎo)得到復(fù)雜薄壁箱梁斷面的自由扭轉(zhuǎn)常數(shù)，該方法前處理需要過(guò)多的人工參與，不適合計(jì)算機(jī)語(yǔ)言。Lubarda[6]通過(guò)剪力流計(jì)算給出了2室和3室任意薄壁截面的自由扭轉(zhuǎn)常數(shù)表達(dá)式，這種方法無(wú)法應(yīng)對(duì)更復(fù)雜的多室薄壁截面。Loighlan等[7?8]將圖論法的理論引入計(jì)算程序的前處理部分。這種方法編程容易實(shí)現(xiàn)，但計(jì)算量龐大，消耗大量計(jì)算時(shí)間。周建春等[9]通過(guò)比擬有限元方法，建立了求解截面扇性坐標(biāo)等幾何特性的計(jì)算機(jī)算法，但是沒(méi)有給出自由扭轉(zhuǎn)常數(shù)的數(shù)值解法。ANSYS采用有限元網(wǎng)格劃分的計(jì)算方法，這種方法在出現(xiàn)大量的小銳角網(wǎng)格時(shí)便無(wú)法求解，手動(dòng)劃分又費(fèi)時(shí)費(fèi)力[5]。徐秀麗等[10]通過(guò)對(duì)薄壁箱形截面桿件扭轉(zhuǎn)特性進(jìn)行分析，提出利用空間有限元分析軟件的分析功能來(lái)計(jì)算薄壁箱梁截面幾何特性參數(shù)的新途徑，這種計(jì)算方法雖然簡(jiǎn)便，但不是一種精確方法。在此，本文作者根據(jù)復(fù)雜薄壁截面剪力流計(jì)算理論，采用具有寬度的線(xiàn)段進(jìn)行建模，根據(jù)剪力流進(jìn)行列式，給出精確計(jì)算薄壁截面自由扭轉(zhuǎn)常數(shù)的數(shù)值計(jì)算方法，并編寫(xiě)相應(yīng)程序。該方法無(wú)論怎樣指定互斥的剪力流方式，都能得到相同的解答。最后把計(jì)算結(jié)果與Midas軟件計(jì)算結(jié)果進(jìn)行對(duì)比，顯示了本文計(jì)算方法的優(yōu)越性。

1 模型建立和理論推導(dǎo)

1.1 基本假定

任意復(fù)雜薄壁截面自由扭轉(zhuǎn)常數(shù)的計(jì)算滿(mǎn)足經(jīng)典的符拉索夫和烏曼斯基創(chuàng)建的基礎(chǔ)理論。符拉索夫關(guān)于桿件斷面無(wú)畸變的理論適用于開(kāi)口斷面，烏曼斯基的斷面無(wú)畸變理論則可用于閉口斷面，但后來(lái)符拉索夫又創(chuàng)建了斷面有畸變的理論，既能用于閉口又能用于開(kāi)口薄壁桿件[11?12]。閉口薄壁截面自由扭轉(zhuǎn)的基本假定如下：

（1） 橫斷面的周邊不變形，即無(wú)畸變；

（2） 剪應(yīng)力沿壁寬均勻分布且平行于各薄壁周界；

（3） 材料為線(xiàn)彈性材料。

1.2 模型建立

任意開(kāi)閉口薄壁截面的特點(diǎn)是壁寬相對(duì)壁長(zhǎng)非常小，如果按照實(shí)際截面尺寸采用雙線(xiàn)條建立模型，將截面劃分的工作量較大[13?14]，因此，本文的薄壁截面采用了一系列具有寬度的線(xiàn)段來(lái)表示，1條線(xiàn)段代表1個(gè)微元，并由此開(kāi)發(fā)了前處理程序和界面，可以直接讀取CAD數(shù)據(jù)文件，符合工程設(shè)計(jì)人員的習(xí)慣，便于實(shí)際工程應(yīng)用。圖1所示為蘇通大橋某斷面的圖形導(dǎo)入界面，該前處理可以完成圖形的CAD導(dǎo)入、編輯線(xiàn)段、編輯回路、編輯線(xiàn)寬、文件保存以及計(jì)算薄壁截面特性等多項(xiàng)功能。

1.3 理論推導(dǎo)

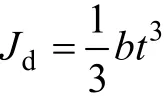
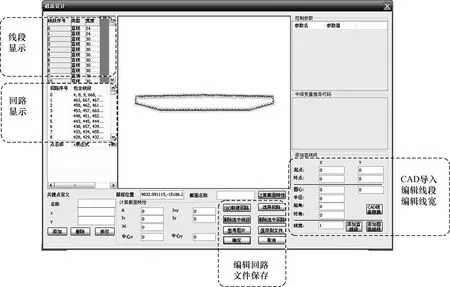
圖1 圖形導(dǎo)入界面Fig.1 Graphic import interface

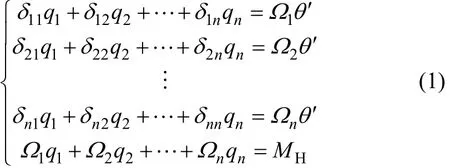
（1） 如圖2（a）所示，12邊是剪力流回路1和剪力流回路2的公共邊，這2個(gè)剪力流在回路中的方向是相反的，取負(fù)號(hào)。

（2） 如圖2（b）所示，12邊是剪力流回路1和剪力流回路2的公共邊，這2個(gè)剪力流在回路中的方向是相同的，取正號(hào)。

最后，自由扭轉(zhuǎn)常數(shù)計(jì)算公式為：

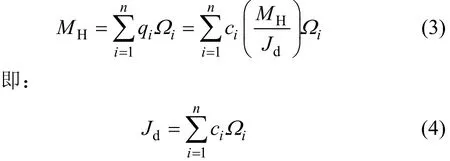
對(duì)于復(fù)雜薄壁截面，同時(shí)存在開(kāi)閉口截面的計(jì)算

公式為：

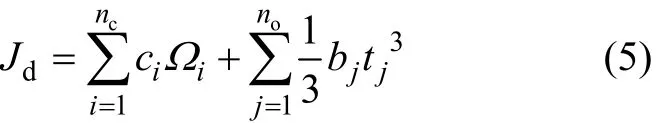
式中：nc為閉合回路數(shù)；no為開(kāi)口薄壁邊數(shù)。

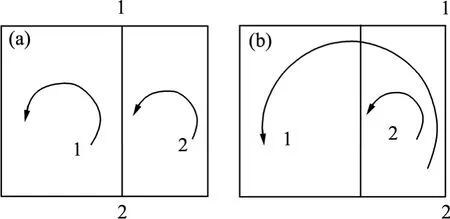
圖2 剪力流示意圖Fig.2 Schematic diagrams of shear flow

2 算例

根據(jù)上述計(jì)算方法編制了計(jì)算程序，并通過(guò)與Midas軟件的計(jì)算結(jié)果進(jìn)行對(duì)比，以驗(yàn)證本文方法的準(zhǔn)確性和穩(wěn)定性。

2.1 閉口薄壁截面自由扭轉(zhuǎn)常數(shù)算例1

閉口薄壁截面尺寸和壁寬見(jiàn)圖3。對(duì)于不同剪力流指定算例的自由扭轉(zhuǎn)常數(shù)計(jì)算結(jié)果見(jiàn)表1。

2.2 閉口薄壁截面自由扭轉(zhuǎn)常數(shù)算例2

截面所有邊的壁寬為1 mm，截面尺寸見(jiàn)圖4。對(duì)于不同剪力流指定算例的自由扭轉(zhuǎn)常數(shù)計(jì)算結(jié)果見(jiàn)表2。

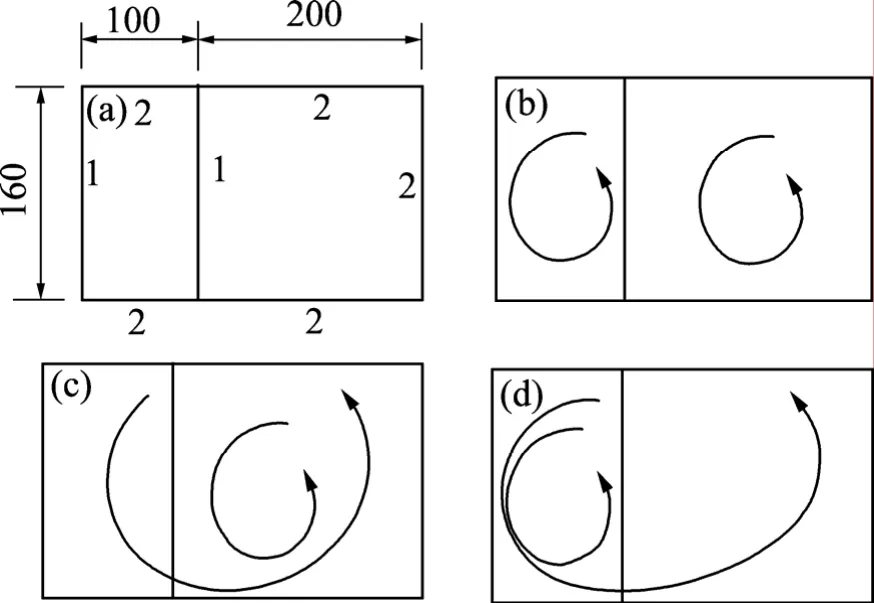
圖3 算例1截面和不同剪力流指定方式Fig.3 Cross-section of example 1 and different modes of shear flow

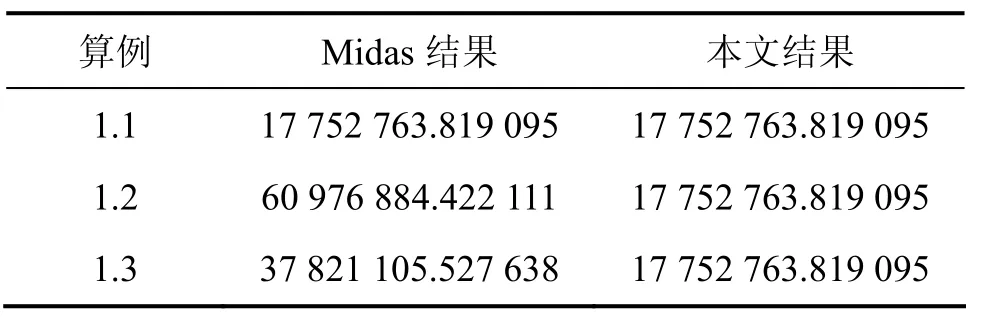
表1 算例1計(jì)算結(jié)果Table 1 Results of example 1 mm4

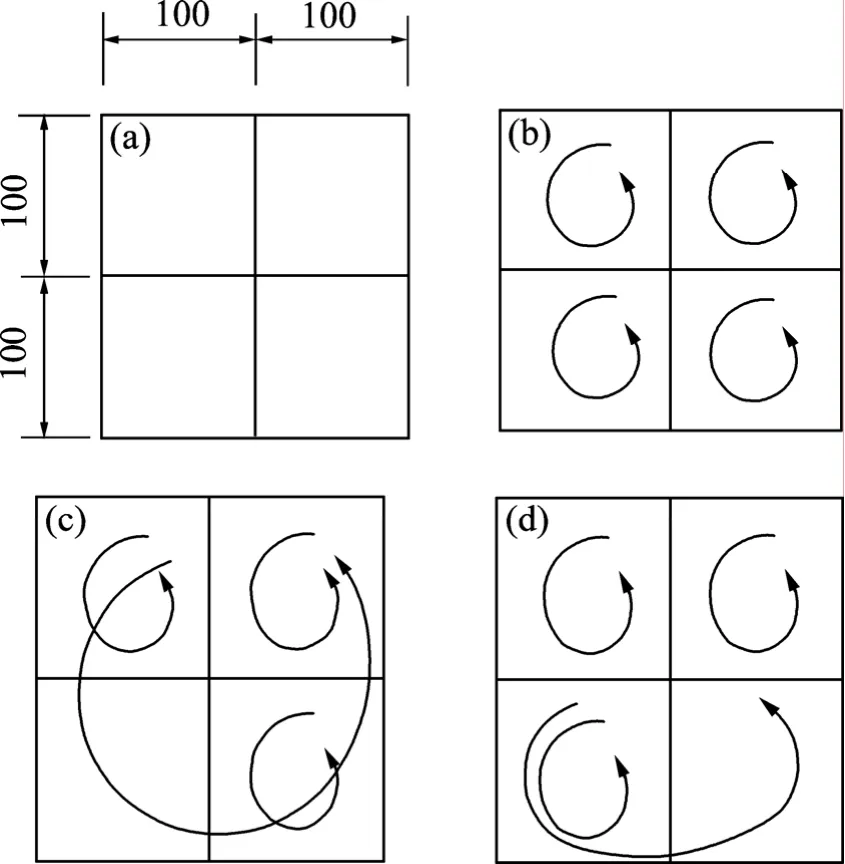
圖4 算例2截面和不同剪力流指定方式Fig.4 Cross-section of example 2 and different modes of shear flow

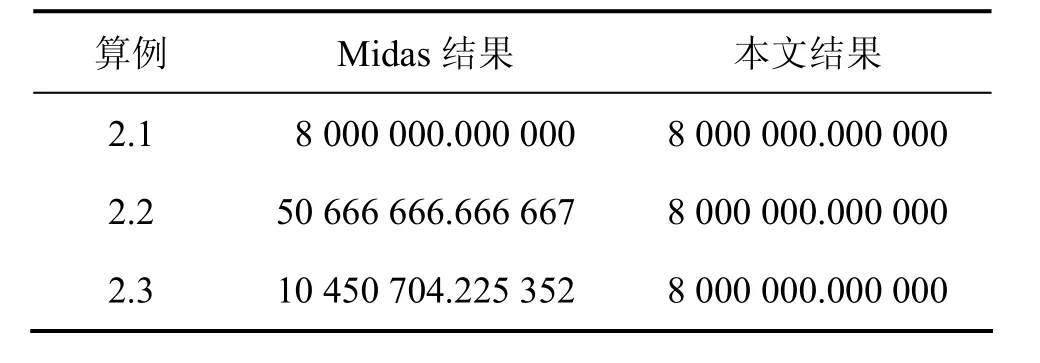
表2 算例2計(jì)算結(jié)果Table 2 Results of example 2 mm4

經(jīng)過(guò)算例1和2的計(jì)算結(jié)果對(duì)比發(fā)現(xiàn)：本文計(jì)算結(jié)果優(yōu)于Midas計(jì)算結(jié)果；對(duì)于任何剪力流指定方式，本文計(jì)算結(jié)果均相同，而Midas計(jì)算結(jié)果出現(xiàn)較大誤差。原因是Midas沒(méi)有考慮不同剪力流指定方式計(jì)算結(jié)果的一致性，導(dǎo)致計(jì)算結(jié)果發(fā)生偏差。

2.3 閉口薄壁截面自由扭轉(zhuǎn)常數(shù)算例3

截面所有尺寸和壁寬見(jiàn)圖5。本文和Midas的自由扭轉(zhuǎn)常數(shù)計(jì)算結(jié)果見(jiàn)表3。

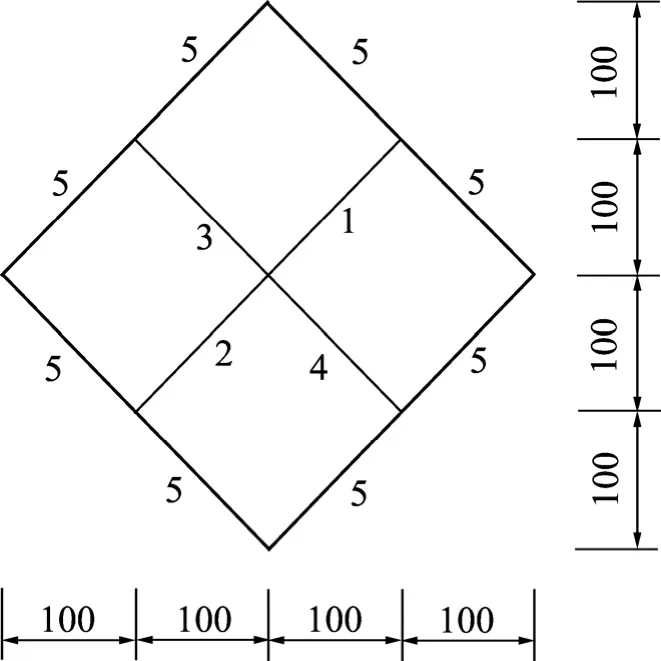
圖5 算例3截面Fig.5 Cross-section of example 3

表3 算例3計(jì)算結(jié)果Table 3 Results of example 3 mm4

2.4 蘇通大橋某截面常數(shù)計(jì)算

圖6所示為蘇通大橋某斷面，表4所示為本文和Midas的計(jì)算結(jié)果。從表4可以看出：本文計(jì)算方法和程序真實(shí)、可信。

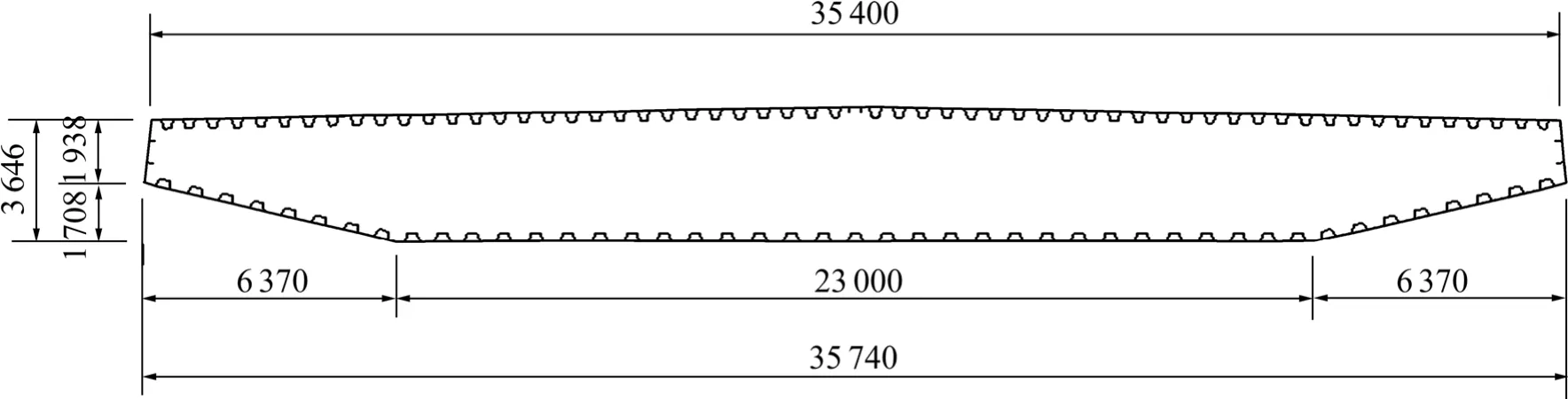
圖6 蘇通大橋某斷面（底板和頂板厚度為20 mm；U肋厚度為8 mm）Fig.6 Cross-section of Suzhou—Nantong Yangtze Road Bridge

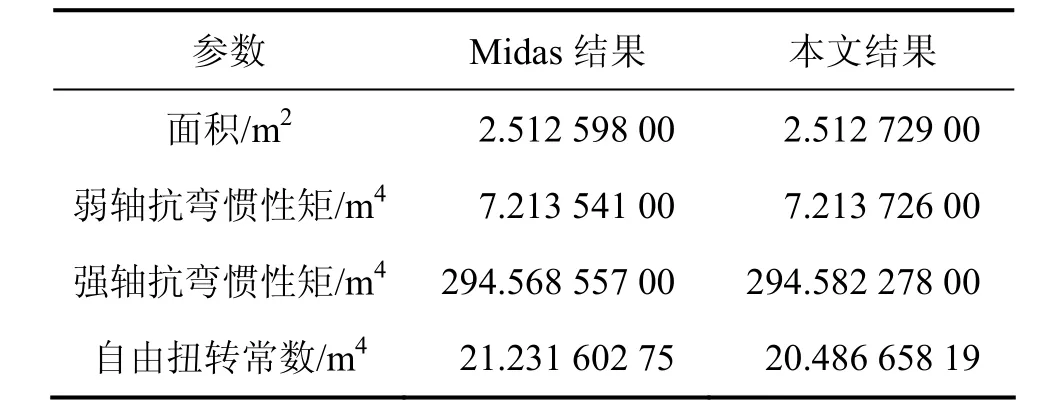
表4 蘇通大橋截面計(jì)算結(jié)果Table 4 Results of Suzhou—Nantong Yangtze Road Bridge

3 結(jié)論

（1） 采用一系列具有寬度的線(xiàn)段建立基本模型，可以直接讀取CAD數(shù)據(jù)文件，實(shí)現(xiàn)了與CAD的無(wú)縫連接，便于工程應(yīng)用。

（2） 根據(jù)薄壁截面剪力流計(jì)算理論，編寫(xiě)相應(yīng)計(jì)算程序，精確計(jì)算了任意復(fù)雜薄壁截面的自由扭轉(zhuǎn)常數(shù)，并把該計(jì)算程序運(yùn)用于大型橋梁結(jié)構(gòu)蘇通大橋的計(jì)算中，得到良好的計(jì)算效果。

（3） 本文計(jì)算程序?qū)τ诓煌袅α髦付ǚ绞降挠?jì)算結(jié)果一致，體現(xiàn)了本文計(jì)算理論和方法的精確性和穩(wěn)定性。

[1] Cheng S H, Lau D T, Cheung M S. Comparison of numerical techniques for 3D flutter analysis of cable-stayed bridges[J]. Computers and Structures, 2003, 81（32）： 2811?2822.

[2] 楊霞林, 李喬, 冉琦山. 斜拉橋雙箱單室箱形主梁的空間應(yīng)力分析[J]. 中國(guó)公路學(xué)報(bào), 2006, 19（1）： 71?74.

YANG Xia-lin, LI Qiao, RAN Qi-shan. Three dimensional stress analysis of main box girder with twin-box single cross section used in cable-stayed bridge[J]. China Journal of Highway and Transport, 2006, 19（1）： 71?74.

[3] Hiroaki K. Consideration of the problem of shearing and torsion of thin-walled beams with arbitrary cross-section[J]. Thin-walled Structures, 2001, 39（8）： 671?684.

[4] Aleksandar P. Computer program for determination of geometrical properties of thin-walled beams with open-closed section[J]. Computers and Structures, 2000, 74（6）： 705?715.

[5] 杜柏松, 葛耀君, 周崢. 復(fù)雜薄壁截面的自由扭轉(zhuǎn)慣性矩的數(shù)值分析[J]. 同濟(jì)大學(xué)學(xué)報(bào)： 自然科學(xué)版, 2006, 34（9）： 1170?1174.

DU Bai-song, GE Yao-jun, ZHOU Zheng. Numerical analysis of free torsion constant for complicated thin-walled cross section[J]. Journal of Tongji University： Natural Science, 2006, 34（9）： 1170?1174.

[6] Lubarda V A. On the torsion constant of multicell profiles and its maximization with respect to spar position[J]. Thin-Walled Structures, 2009, 47（6/7）： 798?806.

[7] Loighlan J, Ahmed M N. Multi-cell carbon fibre composite box beams subjected to torsion with variable twist[J]. Thin-Walled Structures, 2008, 46（7/9）： 914?924.

[8] 湯建宏, 聶孟喜, 梁應(yīng)辰. 復(fù)雜薄壁建筑物斷面特性判定及幾何參數(shù)的圖論處理[J]. 水運(yùn)工程, 2006（3）： 13?17.

TANG Jian-hong, NIE Meng-xi, LIANG Ying-chen. Characteristics judgment and graph theory disposal of geometric parameters in complex thin-walled structures’ section[J]. Part and Waterway Engineering, 2006（3）： 13?17.

[9] 周建春, 劉光棟, 魏琴. 薄壁桿件截面幾何特性計(jì)算的比擬有限元法[J]. 工程力學(xué), 2002, 19（1）： 38?41.

ZHOU Jian-chun, LIU Guang-dong, WEI Qin. An analogous model for finite element analysis of sectional properties of thin-walled bars[J]. Engineering Mechanics, 2002, 19（1）： 38?41.

[10] 徐秀麗, 王曙光, 劉偉慶, 等. 薄壁箱梁截面抗扭參數(shù)的簡(jiǎn)化計(jì)算方法[J]. 中國(guó)公路學(xué)報(bào), 2007, 20（2）： 72?76.

XU Xiu-li, WANG Shu-guang, LIU Wei-qing, et al. Simplified calculation method for torsion parameters of thin-walled box girder section[J]. China Journal of Highway and Transport, 2007, 20（2）： 72?76.

[11] 李明昭, 周競(jìng)歐. 薄壁桿結(jié)構(gòu)計(jì)算[M]. 北京： 高等教育出版社, 1992： 45?79.

LI Ming-zhao, ZHOU Jing-ou. Calculation of thin-walled bar structures[M]. Beijing： Higher Education Press, 1992： 45?79.

[12] 范立礎(chǔ). 橋梁抗震[M]. 上海： 同濟(jì)大學(xué)出版社, 1997： 20?28. FAN Li-chu. Bridge anti-seismicity[M]. Shanghai： Tongji University Press, 1997： 20?28.

[13] 胡曉倫, 王慧萍, 陳立山. 兩類(lèi)橋梁構(gòu)件截面的幾何特性計(jì)算[J]. 交通與計(jì)算機(jī), 2005, 23（3）： 86?90.

HU Xiao-lun, WANG Hui-ping, CHEN Li-shan. Calculating geometric characters of two bridge component sections[J]. Traffic and Computer, 2005, 23（3）： 86?90.

[14] 程進(jìn), 江見(jiàn)鯨. 用ANSYS軟件進(jìn)行薄壁梁截面幾何特性的計(jì)算[J]. 交通與計(jì)算機(jī), 2001, 19（增）： 77?78.

CHENG Jin, JIANG Jian-jing. Calculation of geometrical properties of the thin-walled beam by ANSYS software[J]. Traffic and Computer, 2001, 19（S）： 77?78.

[15] 黃劍源. 薄壁結(jié)構(gòu)的扭轉(zhuǎn)分析[M]. 北京： 中國(guó)鐵道出版社, 1983： 61?88.

HUANG Jian-yuan. Torsional analysis for thin-walled structure[M]. Beijing： China Railway Publishing House, 1983： 61?88.

（編輯 楊幼平）

Numerical method of free torsion constant for arbitrary complicated thin-walled cross section

KANG Lan1,2, ZHANG Qi-lin1, WANG Zhong-quan1, WU Jie1
（1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. CCCC Fourth Harbor Engineering Institute Co. Ltd., Guangzhou 510230, China）

An effective algorithm and model building method for free torsion constant calculation of thin-walled bars with arbitrary complicated thin-walled cross sections was presented. Series of lines with given width were used to build the model of thin-walled cross section, corresponding calculation program was developed based on theory of shear flow, and free torsion constant for arbitrary complicated thin-walled cross section was obtained. The calculation theory and method were applied to the world’s largest cable-stayed bridge i.e., Suzhou—Nantong Yangtze Road Bridge, and the results of this paper were compared with Midas. The results show that the model building method in this paper realizes the seamless connection with CAD, and is convenient to engineering application; the same results can be obtained by different given models of shear flow, this method overcomes the shortcomings of Midas, and the validity and stability of the method are verified.

bridge engineering; thin-walled cross section; free torsion constant; numerical method; shear flow

TU 448.213

A

1672?7207（2011）05?1437?05

2010?04?09；

2010?08?12

國(guó)家高技術(shù)研究發(fā)展計(jì)劃（“863”計(jì)劃）項(xiàng)目（2009AA04Z420）

張其林（1962?），男，江蘇海門(mén)人，博士，教授，博士生導(dǎo)師，從事鋼結(jié)構(gòu)研究；電話(huà)：021-65980644；E-mail： zhangqilin@tongji.edu.cn