矩陣分解方法的探究

王群英

(肇慶科技職業技術學院基礎課教學研究部，廣東肇慶 526110)

1 矩陣分解的概述

矩陣是數學中最重要的基本概念之一，是代數學的一個主要研究對象，也是數學研究及應用的一個重要工具。矩陣是線性代數中最為重要的核心內容，很多問題都可以歸結為矩陣并最終通過矩陣解決。在近代數學、工程技術、信息處理、經濟理論管理科學中，也大量涉及到矩陣理論的知識，矩陣分解是實現大規模數據處理和分析的一種有效工具，在工程計算中具有重要的實際意義。矩陣理論自然就是學習和研究上述學科必不可少的基礎之一。另一方面，矩陣理論發展到今天已經形成了一整套的理論和方法，內容非常豐富。矩陣分解是指根據一定的原理用某種算法將一個矩陣分解成若干個矩陣的乘積或者一些矩陣之和，矩陣分解對矩陣理論及近代計算數學的發展起了關鍵的作用。尋求矩陣各種意義下的分解形式，是對與矩陣有關的數值計算和理論都有著極為重要的意義。因為這些分解式的特殊形式，一是能明顯地反映出原矩陣的某些特征;二是分解的方法與過程提供了某些有效的數值計算方法和理論分析依據。這些分解在數值代數和最優化問題的解決中都有著十分重要的角色以及在其它領域方面也起著必不可少的作用。

2 矩陣的分解方法

2.1 矩陣LU分解

LU分解，設A=(aij)是n階可逆矩陣，如果A的對角線下(上)方的元素全為零，即對i＞j，aij =0(對i＜j，aij=0)，則稱矩陣A為上(下)三角矩陣，上三角矩陣和下三角矩陣統稱為三角矩陣。如果有下三角矩陣L和上三角矩陣U，使得A= LU，則稱A能做三角分解，并且稱A=LU為A的三角分解或者LU分解[1]。LU分解的定理:設A是n階非奇異矩陣，則存在唯一的單位下三角矩陣L和上三角矩陣U，使得A=LU的充分必要條件是A的所有順序主子式均非零，即

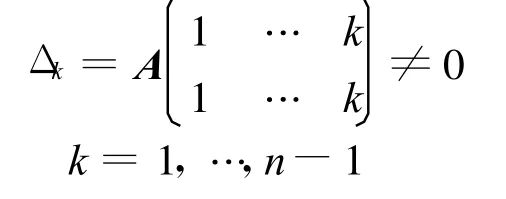
LU分解可以用直接法導出A=LU的分解公式，將A=LU寫成

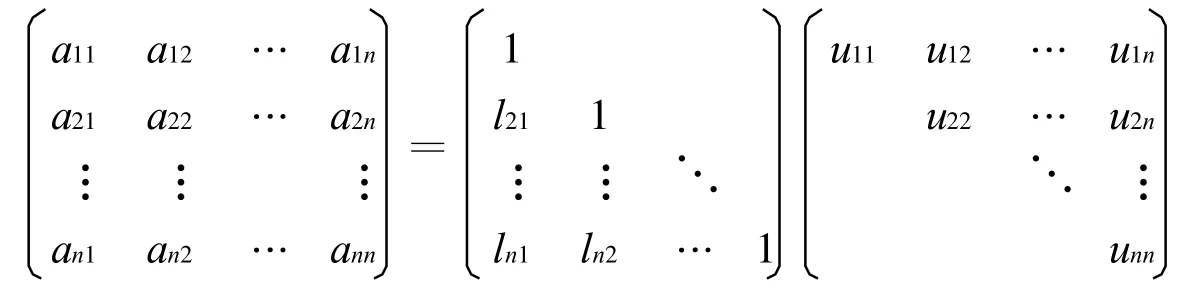
比較等式兩端的第i行和第j列元素，可得

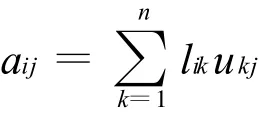
上式利用了lii=1，從而

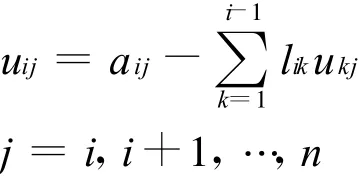
當j=i+1，i+2，…，n時

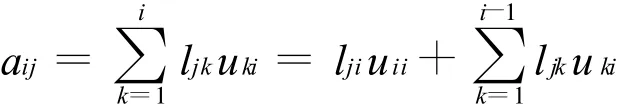
從而

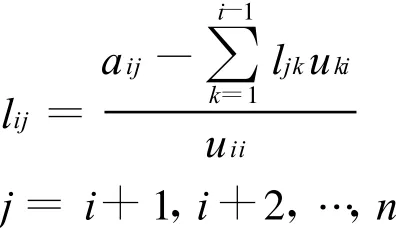
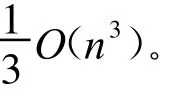
LU分解的初等變換消元法:設可逆矩陣A的n個順序主子式非零，則存在可逆矩陣P，使PA=U，A=P-1U=LU，其中P是一系列初等行矩陣之積(對應于初等行變換)，L=P-1是下三角矩陣，U為上三角矩陣，求P，U可用如下做法:

例1:求矩陣

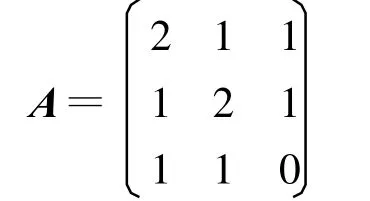
的LU分解。

解:對矩陣(A|I)做初等行變換

可得

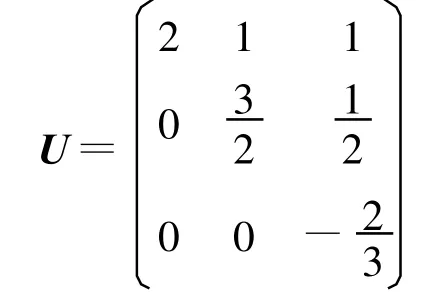
即得A=LU。

2.2 矩陣的QR分解

矩陣的QR分解(正交三角分解)在解決最小二乘問題、特征值計算、廣義逆矩陣的計算方面，都是十分重要的[2]。以下為矩陣的QR分解:設A是n階可逆實矩陣，則A可惟一分解為

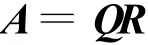
其中，Q為正交矩陣(QTQ=QQT=1，或Q-1= QT)，R是主對角元素都是正數的上三角矩陣，稱該分解為對A的正交三角分解。A是m×n矩陣，且A為列滿秩，即r(A)=n，則有

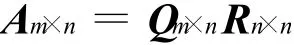
其中，Q m×n的n個列向量是標準正交的，R為正對角元的n階上三角矩陣。

我們看QR分解是不是唯一的。記A= [a1，a2，…，an]，ai是矩陣A的第i個列向量，因為矩陣A非奇異，所以向量組a1，a2，…，an線性無關，應用Gram-Schmidt正交化方法將線性無關向量組a1，a2，…，an化為標準正交向量組q1，q2，…，qn，則可得

則Q為正交(酉)矩陣，R為非奇異實(復)上三角矩陣，由Gram-Schmidt正交分解式，有A=QR，這就證明了QR分解的存在性。

設矩陣A有兩個QR分解

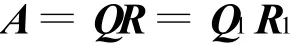
其中，Q，Q1為正交(酉)矩陣，R，R1為非奇異上三角矩陣，則

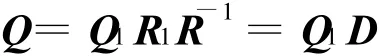
其中，D=R1R-1為非奇異上三角矩陣，于是

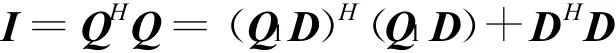
這說明D為酉矩陣，比較等式

的對角元，可導出D為對角矩陣，并且對角元的模全等于1，于是

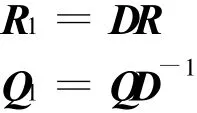
如果在非奇異矩陣A的QR分解中規定上三角矩陣R的各個對角元的符號(例如全為正數)，則A的QR分解是惟一的。

矩陣的QR分解有多種。常見的有Schm idt (施密特)正交分解法、Givens(吉文斯)正交分解法和Household(豪斯霍德)正交分解法。

施密特正交分解法:設可逆矩陣(或列滿秩)A的列向量為α1，α2，…，αn，施以Schmidt標準正交化使β1，β2，…，βn為正交組。

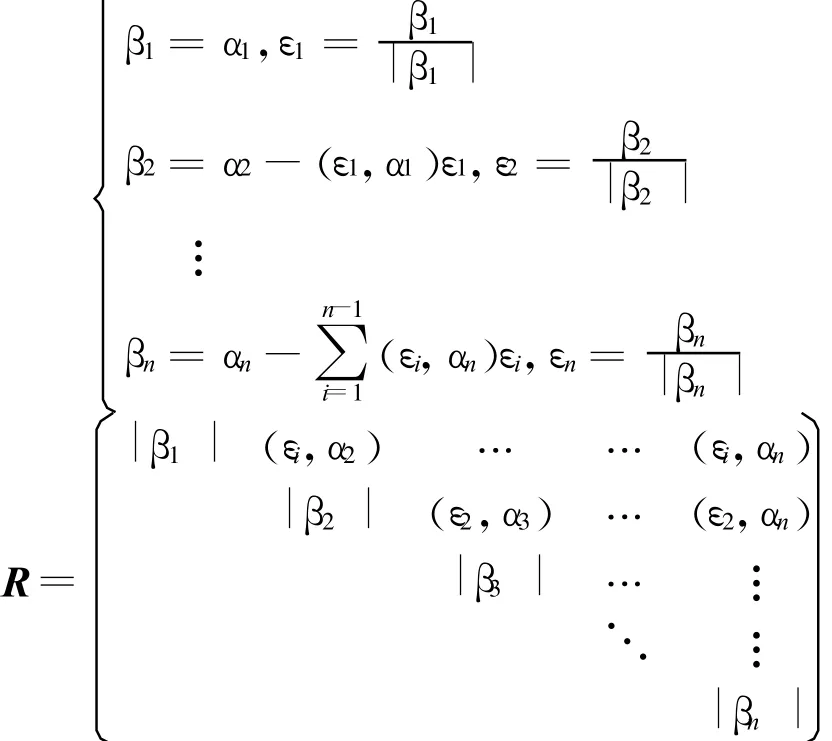
得

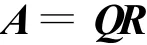
因為ε1，ε2，…，εn為標準正交組，Q=(ε1，ε2，…，εn)為正交陣。

例2:用Schmidt正交化方法求矩陣

的QR分解。

解:令

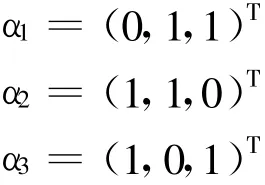
由Schm idt正交化公式，得

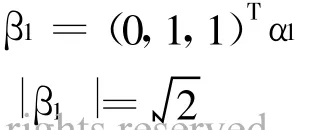
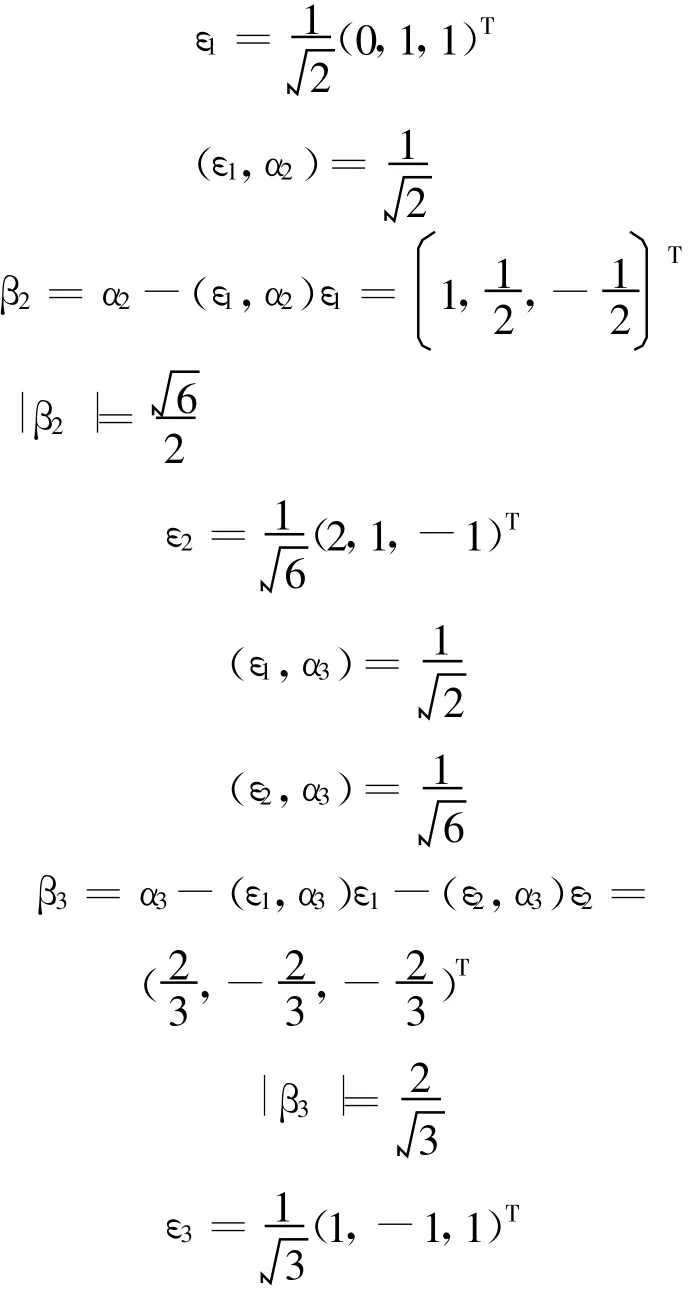
因而可得

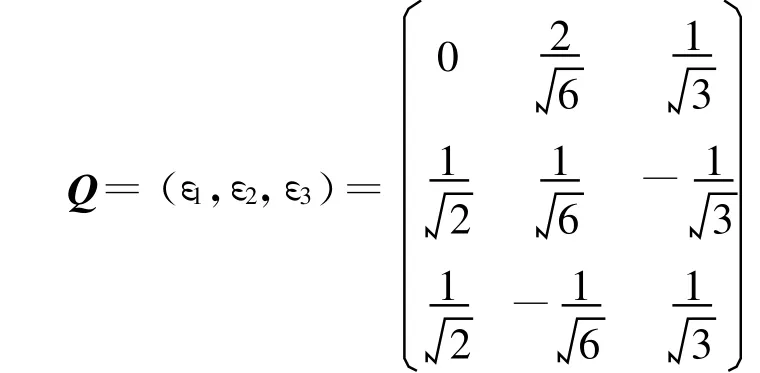
求解公式

得到

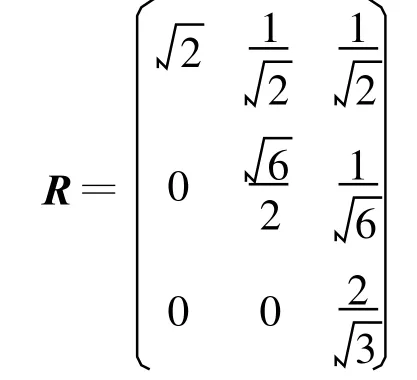
即得

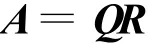
吉文斯方法:利用初等旋轉矩陣的性質，即用Rij左乘矩陣A時，僅影響A的第i行和第j行，且選適當的Rij，就可以消去A的一個非零元素。一般地說，作一次旋轉可以消去一個非零元素。如果在作下一次旋轉時不會影響前面已化為零的元素，即不會重新又變為非零，那么，借助于初等旋轉陣將A約化成上三角陣就有希望。事實上，只要注意運算順序，完全能辦到。

2.3 矩陣的譜分解[3]

2.3.1 單純矩陣的譜分解

n階單純矩陣A有n個線性無關的特征向量，不妨設λ1，λ2，…，λn是A的n個特征值;x1，x2，…，xn是A的n個線性無關的特征向量，且有

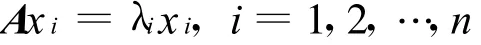
令

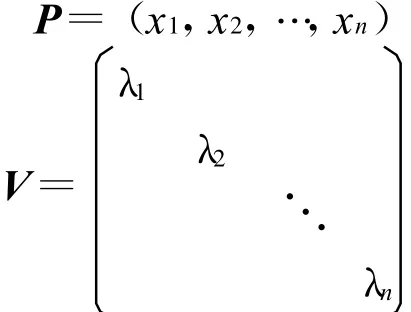
則A=PVP-1兩邊取轉置得AT=(PT)-1VPT，這表明AT也與對角矩陣相似。因此，設y1，y2，…，yn是AT的n個線性無關的特征向量，即

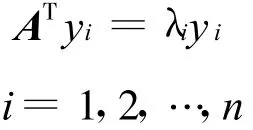
把上式兩端取轉置得

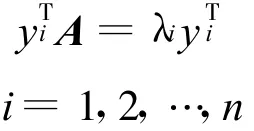
根據上式，我們稱yTi是A的左特征向量，稱xi是A的右特征向量。由式AT=(PT)-1VPT知

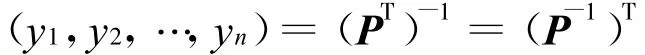
兩端轉置得

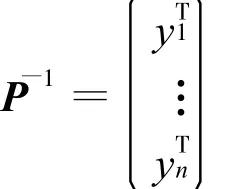
代入

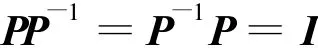
得

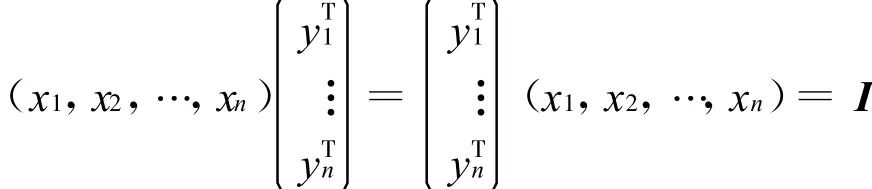
此即

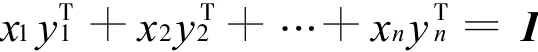
比較兩端即有

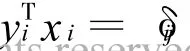
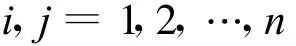
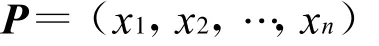
與式

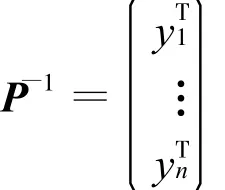
代入A=PVP-1得

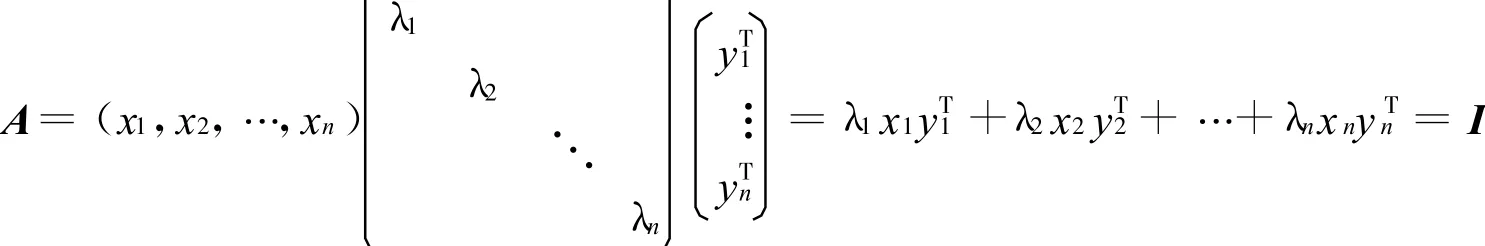
令

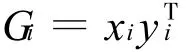
則得

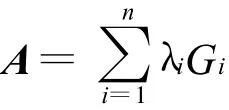
上式稱為單純矩陣A的譜分解。即A分解成n個矩陣Gi之和的形式，其線性組合系數是A的譜(所有的特征值)。

2.3.2 譜分解的相關定理[4]

定理1 設A是n階單純矩陣，λ1，λ2，…，λr是A的r個相異的特征值，則A可以進行滿足下列性質的譜分解[7]。

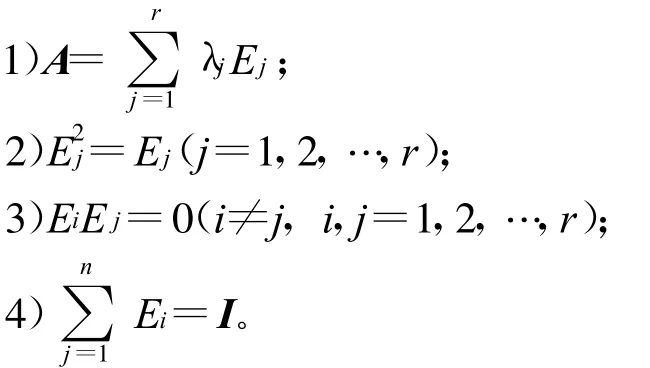
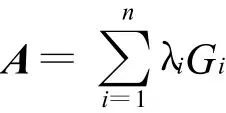
有

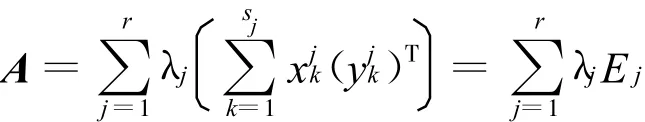
其中

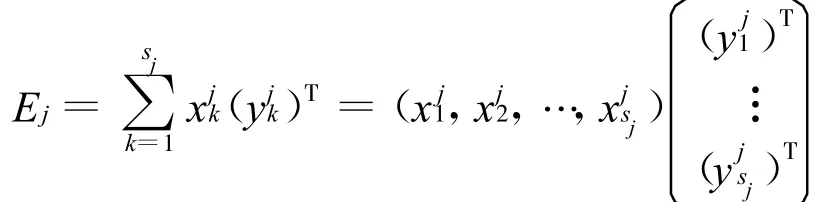
根據式

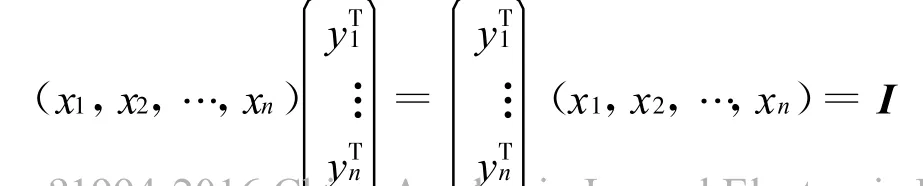
得

再由

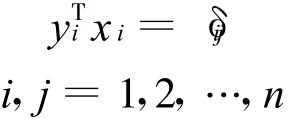
得

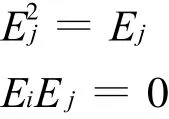
即所有的式子得證。

例3:求矩陣

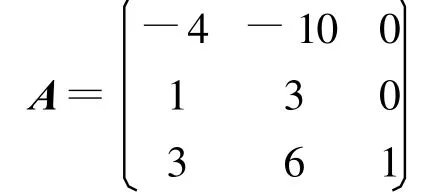
的譜分解。

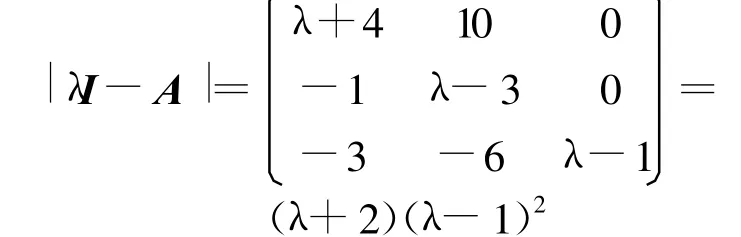
故A的特征值為

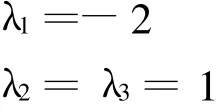
對于λ1=-2，由

得

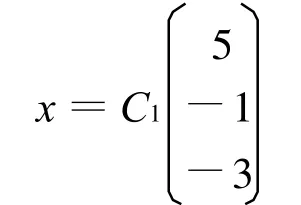
特征向量

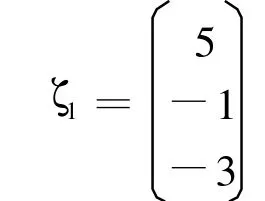
對于λ1=-2，由

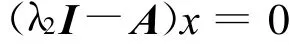
得

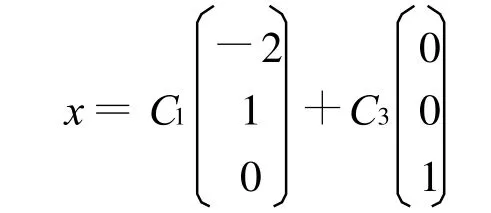
特征向量

所以

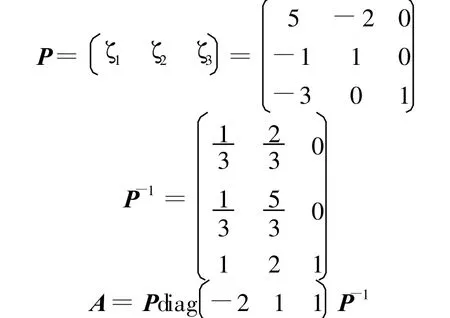
取

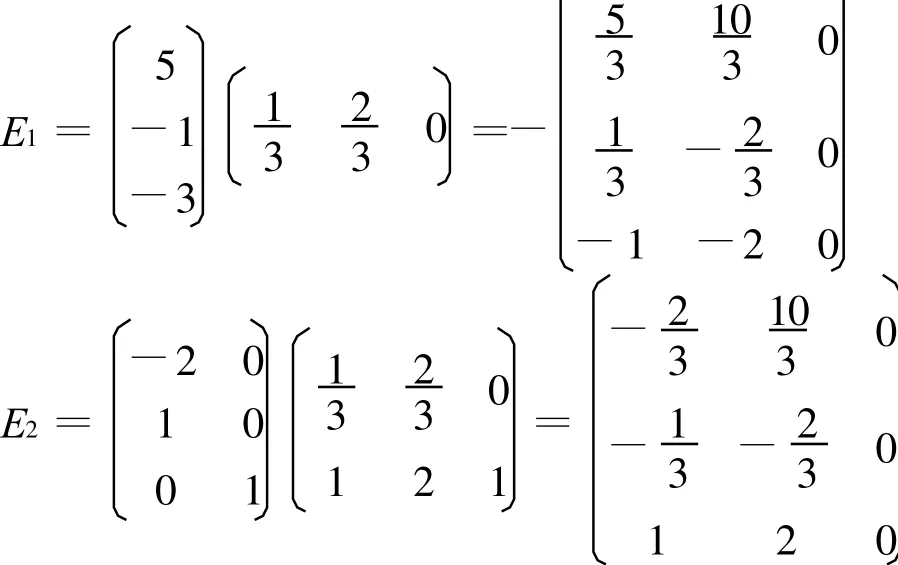
則

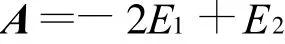
2.4 矩陣的奇異值分解

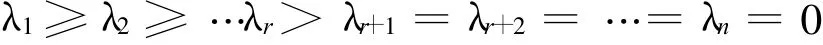
1)m×n矩陣A的奇異值的個數等于列數n (因AHA的階數為n);

2)A的非零奇異值的個數等于 rank A(因rank AHA=rank A)。

以下給出矩陣A的奇異值分解定理。

定理2 設A∈Cm×nr ，則存在m階酉矩陣U和n階酉矩陣V，使得

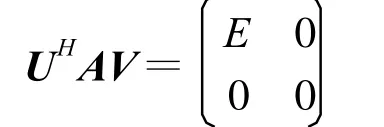
其中E=diag(σ1，σ2，…，σr)，而σi(i=1，2，…，r)為A的正奇異值，稱

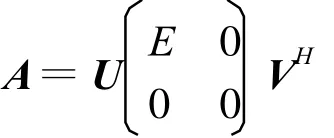
為A的奇異值分解[6]。

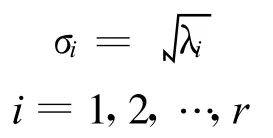
由正規矩陣的充要條件存在n階酉矩陣使得

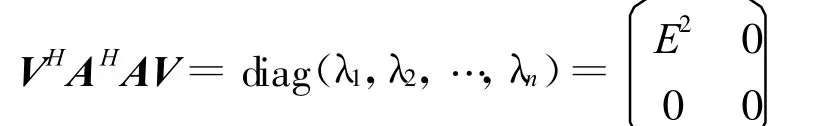
記V=(V1，V2)。其中V1∈Cn×r，V2∈Cn×(n-r)代入上式

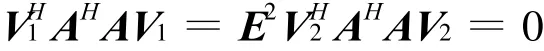
于是

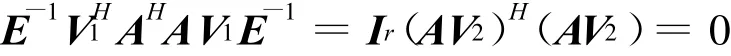
上面第2式說明AV2=0，令U1=AV1 E-1。則由第1式得U1=I說明U1為次酉矩陣，它的r個列向量是兩兩正交的單位向量，取U2∈Cm×(n-r)，使U =(U1，U2)為m階酉矩陣，即

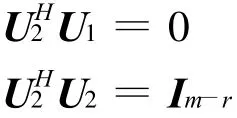
再注意到AV=U1 E，AV2=0，最后有

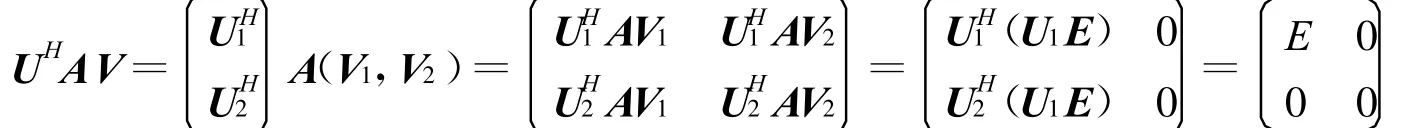
例4:求矩陣

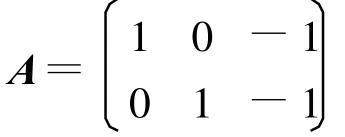
的奇異值分解。

解:因為

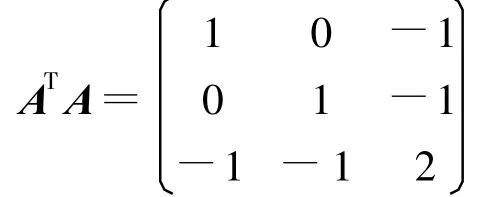
所以ATA得特征值為3，1，0，于是A的奇異值為σ1=，σ2=1且ATA的正交單位特征向量分別為

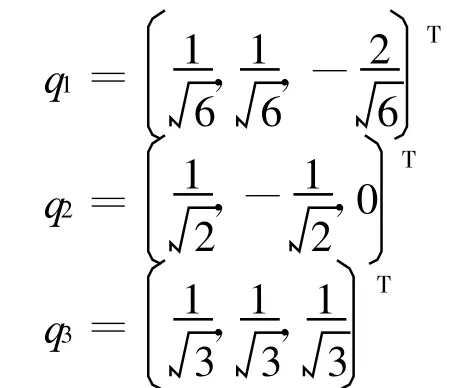
令

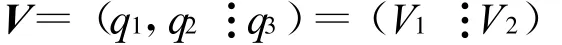
則

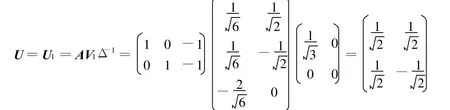
從而可得A的奇異值分解為

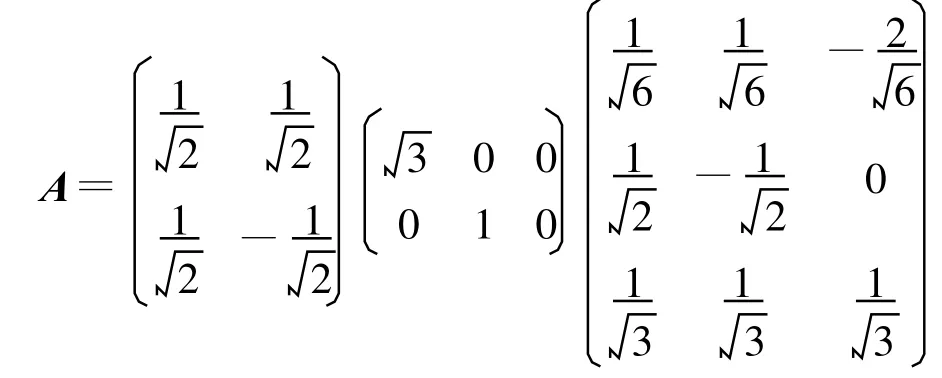
[1] 史榮昌，魏豐.矩陣理論[M].北京:北京理工大學出版社，2008:183-211.

[2] 方保镕，周繼東，李醫民.矩陣論[M].北京:清華大學出版社，2004:291-324.

[3] 戴華.矩陣論[M].北京:科學出版社，2001:117-139.

[4] 李新，何傳江.矩陣理論及其應用[M].重慶:重慶大學出版社，2005:130-145.

[5] 羅小桂.矩陣奇異值分解及其應用[J].井岡山學院學報，2005，12(4):133-135.

[6] D D Lee，H S Seung.Learning the parts the objects with nonnegative matrix factorization[J].Nature，1999，401:213-263.

[7] 李建東.矩陣QR分解的三種方法[J].呂涼學院學報，2009，25(1):16-19.

[8] 徐泰燕，郝玉龍.非負矩陣分解及其應用現狀分析[J].武漢工業學院學報，2010(1):110-115.