二階常微分方程邊值問題的格林函數求法

劉麗環， 常 晶， 高艷超

(空軍航空大學基礎部，吉林長春 130022)

0 引 言

利用拓撲度理論、半序方法以及臨界點理論可以研究常微分方程多個解的存在性，利用不動點定理和單調迭代法可以研究脈沖常微分方程解的存在性。這些年來，這方面的結果有很多[1-5]。格林函數方法是求解常微分方程的一種重要方法，它的實質是把常微分方程加上邊值條件轉化為一個積分方程，通過研究格林函數的性質和函數非線性項的性質求所述的非線性常微分方程邊值問題的解[6-8]。文中主要應用格林函數方法以及壓縮映射原理證明下面二階常微分方程

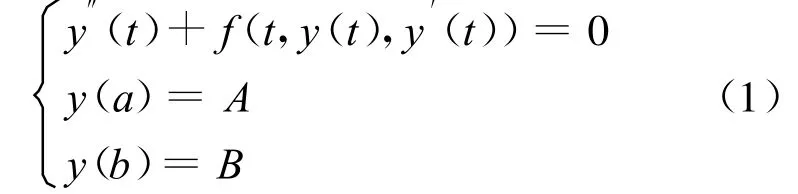
解的存在惟一性。

1 主要結果及證明

定理1 若方程(1)中f(t，y(t)，y′(t))連續，且滿足Lipschitz條件，即

且若

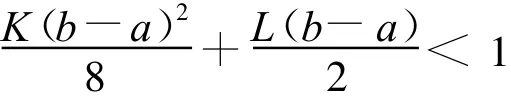
則方程(1)存在惟一解。

證明 首先構造(1)的G reen函數為

則方程(1)等價于

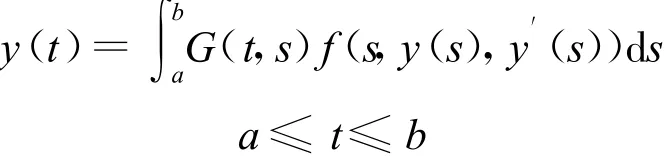
與

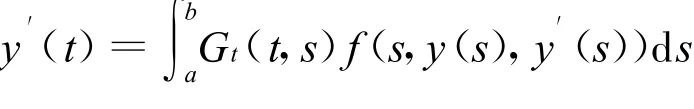
因此

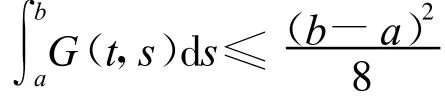
并且

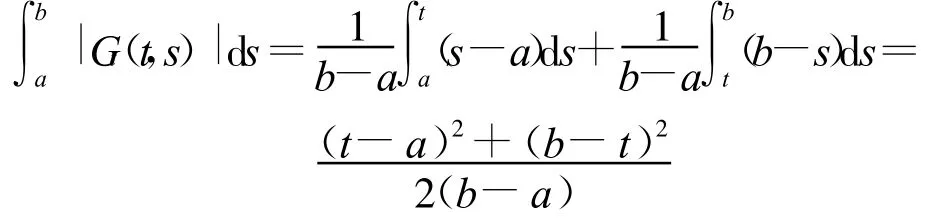
此函數在t=a與t=b處達到最大值，由此可得

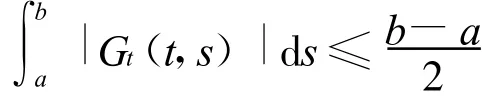
接下來需要尋找一個函數空間，使得y(t)以及y′(t)在此空間下均收斂。取S為[a，b]上的C1函數空間，取u∈S，并定義其范數為:

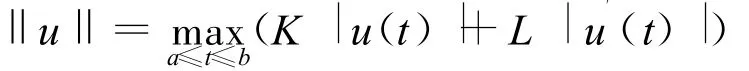
其中K與L為

中的Lipschitz常數。下面需要構造映射 T:S→S，既需要證明:(1)只要u(t)是C′的，則Tu(t)就是C′的;(2)T為壓縮映射。為此構造差商:

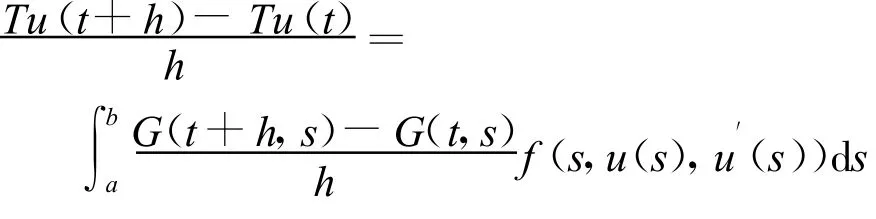
則

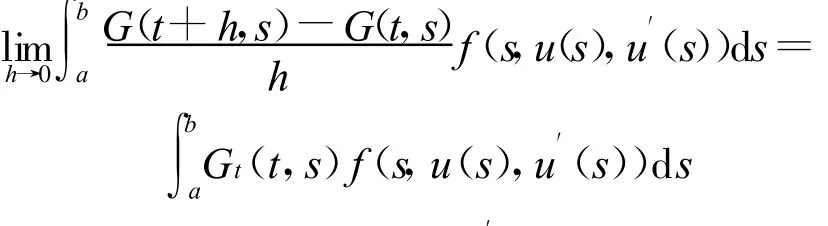
且關于t連續，故Tu(t)就是C′的。我們還需要證明(2)成立。

構造

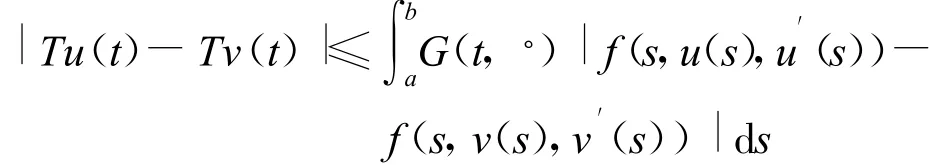
因

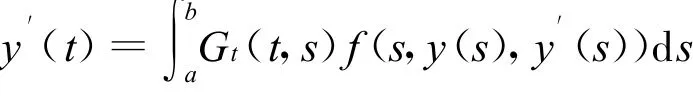
故可以推得

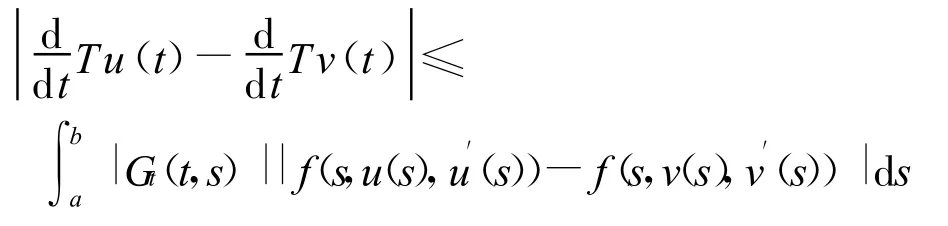
由Lipschitz條件

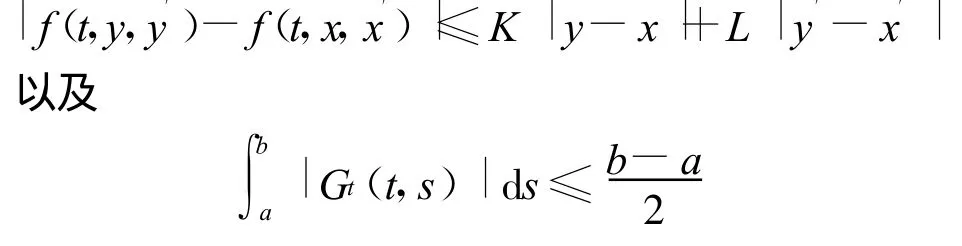
可得。

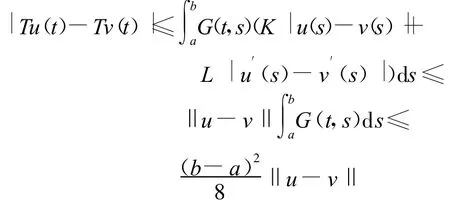
又因

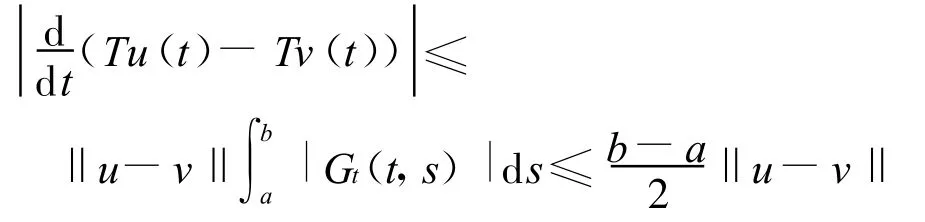
從而

故當

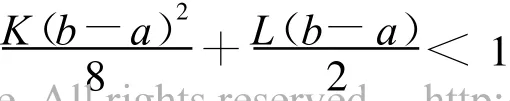
時，‖Tu-Tv‖≤α‖u-v‖，α＜1，故T為壓縮映射，從而方程(1)有惟一解，定理得證。

注1:若方程(1)的邊值條件改為

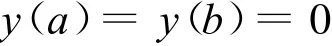
則其相應的G reen函數為:

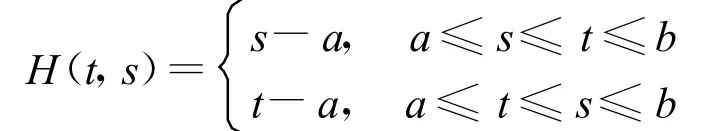
則問題等價于

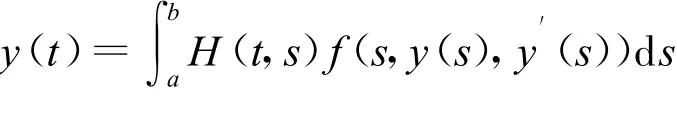
和

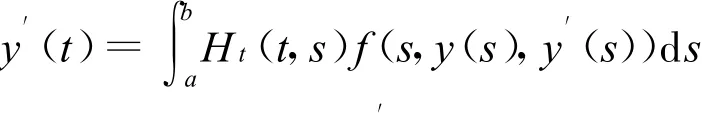
注2:若f中不含有y′時，即

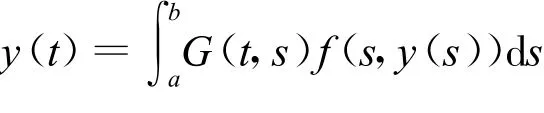
其函數空間S的范數此時可定義為

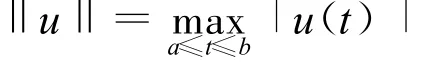
這是S為完備的賦范線性空間，顯然u(t)是連續的，則Tu(t)就是連續的，這意味著T將S映射到自身，接下來確定何時T是S上的一個壓縮映射。首先

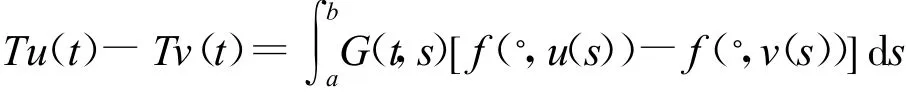
如果使用G(t，s)≥0，及Lipschitz條件

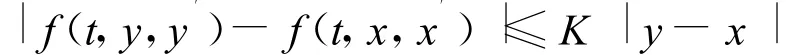
有

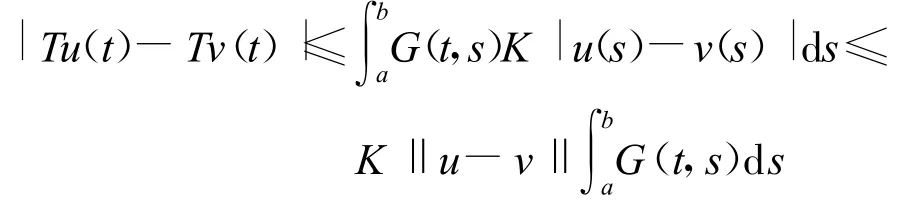
由于

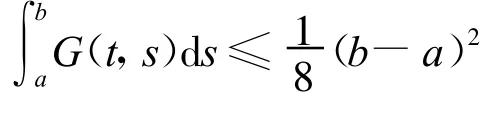
因而

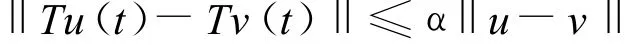
其中

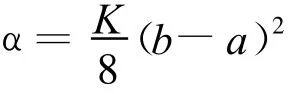
引例:考慮

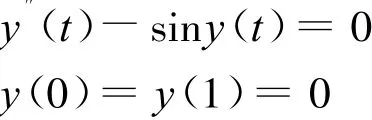
這時

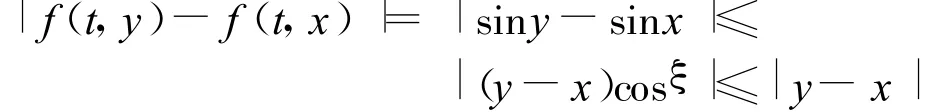
[1] 程綱.二階微分方程邊值問題的多重正解[J].應用數學學報，2003，26(2):272-279.

[2] Dong H SF.Oppenheimer existenceand uniqueness results for some nonlinear boundary value prob lems [J].J.Math.Anal.App l.，1996，198:35-48.

[3] Erbe L H，Kong Q.Boundary value p rob lem s for singular second order functional differential equations[J].J.Comp.App l.M ath.，1994，53:377-388.

[4] LiY.On the existence and nonexistence of positive solutions for nonlinear Strum-Liouville boundary value prob lems[J].J.Math.Ana l.Appl.，2005，304:74-86.

[5] Li Y.Positive so lutions of second order boundary value problem s with sign-changing nonlinear terms [J].J.M ath.Anal.App l.，2003，282:232-240.

[6] Liu Yan Sheng，Yu H ui M in.Existence and uniqueness of positive solution for singular boundary value p roblem[J].Computers and M athematics with A pp lications，2005，50:133-143.

[7] BaiZhan Bing，GeW eiGao.Existence of three positive solutions for some second order boundary value problems[J].Computers and Mathematics with App lications，2004，48:699-707.

[8] Li Fu Y i，Zhang Q i，Liang Zhao Ping.Existence and multip licity of solutions of a kind of fourth order boundary value p rob lem[J].Nonlinear Analysis，2005，62:803-816.