量子粒子群算法優(yōu)化鋼結(jié)構(gòu)截面

譚德坤

(南昌工程學(xué)院計(jì)算機(jī)系,江西南昌 330099)

0 前言

近年來,鋼結(jié)構(gòu)在各行各業(yè)取得了廣泛的應(yīng)用,它是現(xiàn)代建筑工程中較普通的結(jié)構(gòu)形式之一。鋼結(jié)構(gòu)除了在綜合經(jīng)濟(jì)指標(biāo)上具有競爭力之外,還符合社會可持續(xù)發(fā)展關(guān)于材料再利用及環(huán)保的要求,它是一種綠色結(jié)構(gòu)[1]。在合理使用鋼結(jié)構(gòu)的工程中,應(yīng)力求設(shè)計(jì)出先進(jìn)、合理,盡量降低鋼材消耗,并能保證可靠性要求的結(jié)構(gòu)。傳統(tǒng)的剛結(jié)構(gòu)基本構(gòu)件截面設(shè)計(jì)中,由于涉及到的未知量太多,截面設(shè)計(jì)時往往采用試算法,首先根據(jù)已有工程經(jīng)驗(yàn)進(jìn)行初選,然后再進(jìn)行各項(xiàng)驗(yàn)算,驗(yàn)算不合適時,則調(diào)整截面尺寸,繼續(xù)重新驗(yàn)算,直到滿足設(shè)計(jì)要求為止。由于計(jì)算復(fù)雜,初選截面尺寸大多不一定合適,因而需要進(jìn)行多次調(diào)整才能得到比較滿意的截面[2-3]。該過程常采用手算,計(jì)算量大,計(jì)算過程中費(fèi)時費(fèi)力,而且容易出錯,對工程技術(shù)人員而言,是一項(xiàng)比較辛苦而繁瑣的工作。隨著計(jì)算機(jī)的日益普及和優(yōu)化算法的快速發(fā)展,通過電腦編程對構(gòu)件進(jìn)行快速、準(zhǔn)確的優(yōu)化計(jì)算,從而減輕工程技術(shù)人員的勞動強(qiáng)度,已經(jīng)成為工程結(jié)構(gòu)設(shè)計(jì)領(lǐng)域中的新趨勢。

目前,已有不少學(xué)者對鋼結(jié)構(gòu)截面的優(yōu)化設(shè)計(jì)進(jìn)行了研究,如熊義泳等給出了一系列鋼結(jié)構(gòu)基本構(gòu)件截面設(shè)計(jì)的簡化算法[2,4-5],上述文獻(xiàn)中所提簡化算法的核心都是根據(jù)工程設(shè)計(jì)要求初選截面參數(shù),從而提高所選截面的準(zhǔn)確性,減少試算次數(shù),設(shè)計(jì)出較為合理的優(yōu)選截面。文獻(xiàn)[6-8]也探討了不同鋼構(gòu)件截面的快速優(yōu)化方法,文獻(xiàn)[6]通過簡化假定,給出了截面特性的簡化計(jì)算表達(dá)式,但計(jì)算假定與工程實(shí)際有出入;文獻(xiàn)[7]采用準(zhǔn)則優(yōu)化方法,以用鋼量為目標(biāo)函數(shù),通過方程求導(dǎo)直接給出設(shè)計(jì)公式;文獻(xiàn)[8]首先通過作圖法求得初選截面參數(shù),然后通過少量試算獲得理想截面。但是上述研究的著眼點(diǎn)都是為了減少手算次數(shù),是一種基于手算過程的快速算法。鋼結(jié)構(gòu)截面優(yōu)化設(shè)計(jì)問題具有非線性、離散性、不可微、非凸性等特點(diǎn)[9],而進(jìn)化算法是一種具有全局尋優(yōu)能力的智能尋優(yōu)方法,它為解決該類問題提供了一種全新的思路。

粒子群算法(PSO)[10]是Eberhart和Kennedy于1995年提出的一種集群智能優(yōu)化算法。在深入研究 PSO算法單個粒子收斂行為的基礎(chǔ)上,文獻(xiàn)[11]從量子力學(xué)的角度出發(fā)提出了量子粒子群優(yōu)化算法(QPSO)。QPSO算法的特點(diǎn)是計(jì)算簡單、容易實(shí)現(xiàn)、控制參數(shù)少,它比標(biāo)準(zhǔn)PSO算法具有更強(qiáng)的全局搜索能力。

本文就是利用量子粒子群算法來進(jìn)行鋼構(gòu)件截面選擇時的優(yōu)化計(jì)算,該方法計(jì)算精度高,收斂速度快,是一種有效的鋼結(jié)構(gòu)截面優(yōu)化計(jì)算方法。

1 量子粒子群優(yōu)化算法

1.1 約束優(yōu)化模型描述

非線性約束優(yōu)化設(shè)計(jì)模型可以描述為[12]:

設(shè)計(jì)變量:X=[x1,x2,…,xn]T。

目標(biāo):min f(X)。

約束:ai≤xi≤bi(i=1,2,…,n);

hj(X)=0(j=1,2,…,p);

gk(X)≤0(k=1,2,…,l),

式中,ai、bi為第i個設(shè)計(jì)變量xi的上、下限;n為設(shè)計(jì)變量的個數(shù);p為等式約束的個數(shù);l為不等式約束的個數(shù)。

1.2 量子粒子群算法

量子粒子群算法是在PSO算法的基礎(chǔ)上,結(jié)合了量子力學(xué)中粒子在一維δ勢阱中的運(yùn)動規(guī)律而提出的新的全局優(yōu)化算法。在量子世界中,粒子運(yùn)動軌跡不受限制,只隨時間演化,它可以在整個可行解空間中進(jìn)行搜索,因而QPSO算法的全局搜索性能遠(yuǎn)遠(yuǎn)優(yōu)于標(biāo)準(zhǔn)PSO算法。與PSO算法不同,在QPSO算法中,粒子按照下列公式更新位置[11,13]:

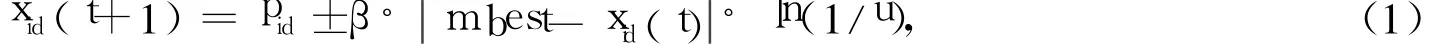
式(1)表示通過蒙特卡羅隨機(jī)模擬方式得到粒子的位置方程,β稱為收縮-擴(kuò)張因子,它是 QPSO的一個重要參數(shù),第T次迭代時可取β=0.5(MaxIter-T)/MaxIter,MaxIter是總的迭代次數(shù);u為(0,1)范圍內(nèi)變化的隨機(jī)數(shù);pid和mbest分別由如下兩式求得。

為了保證算法的收斂性,每一個粒子必須收斂于各自的p點(diǎn),p=(p1,p2,…,pd),第i個粒子 p點(diǎn)的第d維坐標(biāo)為:

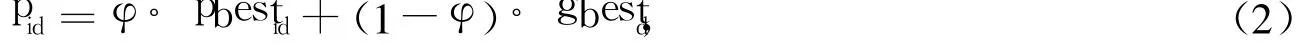
式中,φ是(0,1)之間的隨機(jī)數(shù);pid是介于pbest和gbest之間的隨機(jī)位置。

式中,mbest是所有粒子當(dāng)前最優(yōu)位置的中心點(diǎn);M為種群規(guī)模。

從上述方程可以看出:QPSO與PSO明顯的區(qū)別是前者引入了粒子位置的隨機(jī)指數(shù)分布,它使得粒子在每一個迭代步的搜索空間是整個可行解空間,增強(qiáng)了搜索全局最優(yōu)解的能力。同時又引入了mbest的信息,它使得QPSO的收斂性能大大提高,原因是個體間的協(xié)調(diào)性更強(qiáng),單個粒子不能獨(dú)自收斂,必須等待其他粒子。

1.3 算法描述

從前述分析可以看出QPSO算法是一種全局優(yōu)化算法,其具體步驟如下:

(Ⅰ)設(shè)定初始參數(shù),產(chǎn)生初始種群。

(Ⅱ)計(jì)算粒子的當(dāng)前適應(yīng)度值,并與前一次迭代的值進(jìn)行比較,如果當(dāng)前適應(yīng)度值比前一次的小,則更新粒子的當(dāng)前位置,即如果f(xi(t+1))＜f(pi(t)),則pi(t+1)=xi(t+1)。

(Ⅲ)計(jì)算平均最優(yōu)位置mbest。

(Ⅳ)計(jì)算群體的當(dāng)前全局最優(yōu)位置,并與前一次迭代的全局最優(yōu)位置比較,若當(dāng)前全局最優(yōu)位置較好,則更新種群的全局最優(yōu)位置。

(Ⅴ)對粒子的每一維,根據(jù)式(2)計(jì)算隨機(jī)點(diǎn)位置pi,并根據(jù)式(1)計(jì)算粒子的新位置。如果某一粒子飛出搜索空間(即違反約束條件),則令該粒子的位置大小等于其邊界值,并令其速度乘以-1,以使該粒子向相反的方向搜索。

(Ⅵ)檢驗(yàn)是否符合結(jié)束條件:若達(dá)到迭代停止條件(當(dāng)前迭代次數(shù)達(dá)到最大迭代次數(shù)或者最優(yōu)解達(dá)到最小誤差要求),則算法結(jié)束,返回當(dāng)前最優(yōu)個體作為解輸出;否則,轉(zhuǎn)步驟(Ⅱ)。

2 鋼結(jié)構(gòu)基本構(gòu)件優(yōu)化計(jì)算實(shí)例

本文使用QPSO算法對兩個典型的鋼結(jié)構(gòu)截面優(yōu)化問題進(jìn)行了求解。數(shù)值實(shí)驗(yàn)在Matlab平臺下進(jìn)行,種群規(guī)模 N=20,取最大迭代次數(shù)為T=50。并將本文算法的結(jié)果與傳統(tǒng)的試算法及標(biāo)準(zhǔn) PSO算法的結(jié)果進(jìn)行了比較。

算例1 軸心受壓柱截面優(yōu)化計(jì)算問題

如圖1所示,一軸心受壓柱,采用焊接箱型截面,鋼材為 Q235,柱截面無削弱,柱的上下端均為鉸接,柱高6 m,軸心壓力設(shè)計(jì)值為N=6 000 kN(包括柱身自重)[14]。試設(shè)計(jì)該截面。

設(shè)截面參數(shù)為:腹板厚度為x1,高度為 x2,翼緣板寬度為 x3,厚度為 x4。設(shè)軸心壓力為 N,設(shè)計(jì)強(qiáng)度值為f,x方向的計(jì)算長度為lox,y方向的計(jì)算長度為 loy,容許長細(xì)比為[λ],則該截面優(yōu)化計(jì)算的數(shù)學(xué)模型為:

計(jì)算變量:x1,x2,x3,x4。

目標(biāo)函數(shù):minA=2x1x2+2x3x4。

約束條件:

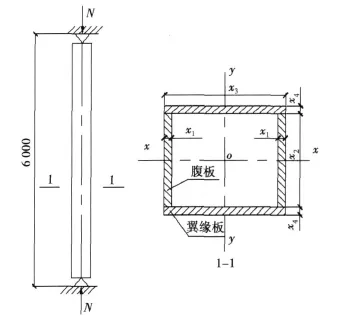
圖1 算例1示意圖

(Ⅲ)剛度要求:[λ]=max{λx,λy}≤150。

(Ⅳ)工程構(gòu)造要求:x1≥4,且 x1、x4取 2的倍數(shù),x2、x3取 10的倍數(shù)。

從以上可以看出:對于鋼構(gòu)件的截面優(yōu)化設(shè)計(jì)問題,其數(shù)學(xué)模型的建立是根據(jù)設(shè)計(jì)規(guī)范[15]和實(shí)際工程的具體要求轉(zhuǎn)化為一系列的約束條件,以一組不等式的形式表達(dá)出來。

量子粒子群算法對該截面優(yōu)化計(jì)算問題進(jìn)行求解,即求解不同的參數(shù) x1,x2,x3,x4,在滿足約束條件的情況下,使面積A最小。在本例中,lox=600 cm,loy=600 cm,fy為鋼材屈服點(diǎn)的標(biāo)準(zhǔn)值,對Q235鋼,fy=235 N/mm2,穩(wěn)定系數(shù)φ由Perry公式[16]求得,長細(xì)比λx,λy由文獻(xiàn)[16]中提供的公式進(jìn)行計(jì)算。本文計(jì)算結(jié)果與 PSO計(jì)算結(jié)果及文獻(xiàn)[14]中的手工試算結(jié)果進(jìn)行了比較,結(jié)果如表1所示。

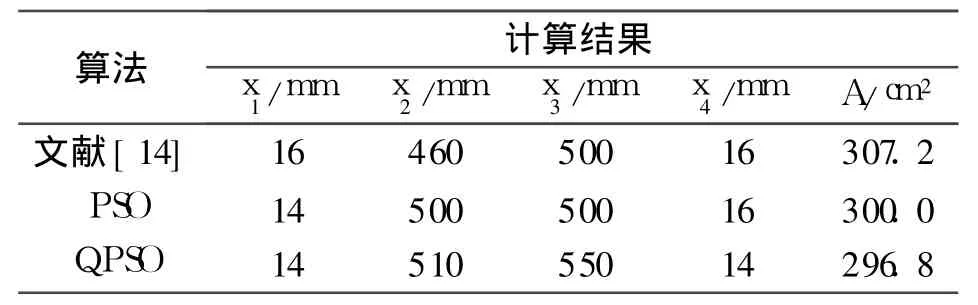
表1 算例1的計(jì)算結(jié)果比較

從表1的結(jié)果可以看出:手工試算結(jié)果最差,這主要是憑設(shè)計(jì)者的個人經(jīng)驗(yàn),經(jīng)驗(yàn)豐富與否對結(jié)果影響很大。PSO計(jì)算結(jié)果其次,原因是其搜索過程中易陷入局部最優(yōu),所得結(jié)果常常是局部最優(yōu)解,未搜尋到全局最優(yōu)解。而QPSO引入了量子特性,可以在整個可行解空間中進(jìn)行搜索,具有較強(qiáng)的全局尋優(yōu)能力,所得計(jì)算結(jié)果均優(yōu)于文獻(xiàn)[14]手工試算結(jié)果及 PSO計(jì)算結(jié)果,在滿足工程要求的前提下,它的經(jīng)濟(jì)性比前者節(jié)省3.5%,比后者節(jié)省1.08%。

算例2 實(shí)腹式單向壓彎構(gòu)件截面優(yōu)化計(jì)算問題

一個 Q235鋼焊接工字形截面壓彎構(gòu)件,兩端鉸接,翼緣板為剪切邊,截面無削弱。承受軸向壓力設(shè)計(jì)值N=880 kN,跨中集中橫向荷載設(shè)計(jì)值F=180 kN。構(gòu)件長l=10 m,橫向荷載作用處有一側(cè)向支撐[14]。試設(shè)計(jì)該截面尺寸。

設(shè)截面參數(shù)為翼緣寬度為b(x1),厚度為t(x2),腹板高度為h0(x3),厚度為tw(x4)。設(shè)軸心壓力為N,設(shè)計(jì)強(qiáng)度值為 f,x方向的計(jì)算長度為 lox,y方向的計(jì)算長度為 loy,容許長細(xì)比為[λ]。翼緣板為剪切邊的焊接工字形截面構(gòu)件對強(qiáng)軸x軸屈曲時屬b類截面,對y軸屬c類截面。根據(jù)文獻(xiàn)[15]的設(shè)計(jì)要求,則建立該截面優(yōu)化設(shè)計(jì)問題的數(shù)學(xué)模型如下:

計(jì)算變量:x1,x2,x3,x4。

目標(biāo)函數(shù):min A=2x1x2+x3x4。

約束條件:

(Ⅰ)彎矩作用平面內(nèi)的整體穩(wěn)定要求(見文獻(xiàn)[15]中5.2.2-1條):

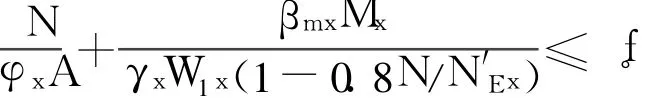
(Ⅱ)彎矩作用平面外的整體穩(wěn)定性要求(見文獻(xiàn)[15]中5.2.2-3條):

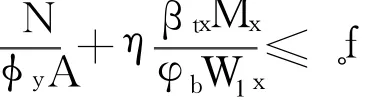
(Ⅲ)翼緣板局部穩(wěn)定性要求(見文獻(xiàn)[15]中5.4.1條):

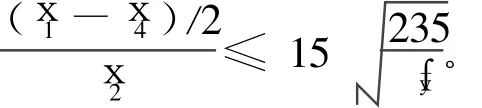
(Ⅳ)腹板局部穩(wěn)定性要求(見文獻(xiàn)[15]中5.4.2條):

當(dāng)0≤a0≤1.6時,

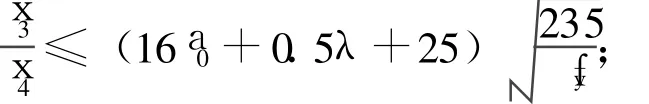
當(dāng)1.6＜a0≤2時,

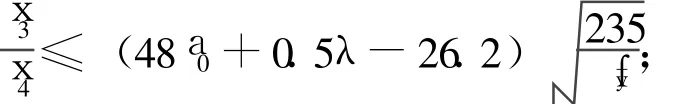
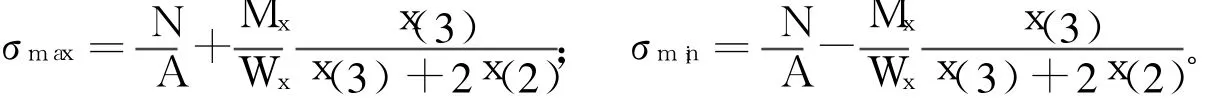
(Ⅴ)剛度要求:[λ]=max{λx,λy}≤150。

(Ⅵ)工程構(gòu)造要求:x4≥4,且 x2、x4取 2的倍數(shù),x1、x3取 10的倍數(shù),它們均為正數(shù)。

用QPSO算法對該截面優(yōu)化計(jì)算問題進(jìn)行了計(jì)算求解,并與PSO算法結(jié)果及文獻(xiàn)[14]的手工計(jì)算結(jié)果進(jìn)行了比較,比較結(jié)果見表2。

從表2中可以看出:在滿足工程約束要求的前提下,QPSO算法得到了較為理想的截面優(yōu)化計(jì)算結(jié)果,其截面面積最小,它的經(jīng)濟(jì)性比文獻(xiàn)[14]計(jì)算結(jié)果節(jié)省 20.3%,比標(biāo)準(zhǔn)粒子群算法的優(yōu)化結(jié)果節(jié)省6.6%,優(yōu)化效果很明顯。

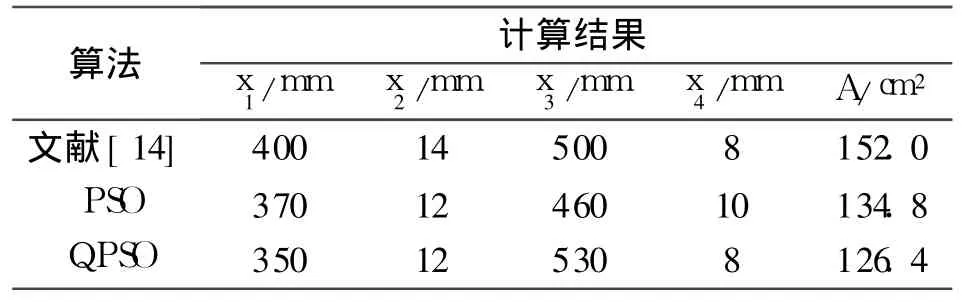
表2 算例2的計(jì)算結(jié)果

從上述兩個優(yōu)化算例的計(jì)算結(jié)果均可以看出:本文算法是實(shí)用、有效的,性能優(yōu)良。

3 結(jié)論

本文將具有群體智能的優(yōu)化算法——PSO算法引入結(jié)構(gòu)工程領(lǐng)域,利用它進(jìn)行鋼結(jié)構(gòu)基本構(gòu)件的優(yōu)化設(shè)計(jì),針對標(biāo)準(zhǔn)PSO算法易早熟收斂的缺陷,用量子特性對PSO算法進(jìn)行了改進(jìn),提出了基于量子特性的QPSO算法。為了驗(yàn)證本文方法的正確性,用兩個典型的鋼結(jié)構(gòu)基本構(gòu)件截面優(yōu)化設(shè)計(jì)算例對其進(jìn)行了驗(yàn)證,從計(jì)算結(jié)果可以看出本文優(yōu)化效果較優(yōu),可用于工程實(shí)際。

致謝:本文在撰寫過程中,南昌工程學(xué)院土木系熊義泳教授對專業(yè)術(shù)語的解釋、作圖規(guī)范等各方面提供了大力幫助,并提供了有關(guān)的國家標(biāo)準(zhǔn)。作者在此表示衷心感謝!

[1] 尚守平.綠色結(jié)構(gòu)工程[M].北京:中國建筑工業(yè)出版社,2009.

[2] 熊義泳.實(shí)腹式型鋼截面壓彎構(gòu)件設(shè)計(jì)的簡化算法[J].建筑結(jié)構(gòu),2006,36(4):68-69.

[3] 吳銀輝.鋼結(jié)構(gòu)軸心受壓截面設(shè)計(jì)方法探討[J].四川建筑,2003,23(6):72-81.

[4] 熊義泳,陳述,羅文海.組合梁截面選擇的一種改進(jìn)設(shè)計(jì)方法[J].南昌工程學(xué)院學(xué)報(bào),2010,29(1):21-24.

[5] 熊義泳,趙江倩.實(shí)腹式組合截面壓彎構(gòu)件的簡化計(jì)算方法[J].工業(yè)建筑,2006,36(7):87-91.

[6] 段樹鑫.焊接工字形鋼梁截面設(shè)計(jì)的直接算法[J].建筑結(jié)構(gòu),1999(11):51-55.

[7] 彭興黔.等邊角鋼四肢方陣式格構(gòu)柱截面的優(yōu)化設(shè)計(jì)[J].華僑大學(xué)學(xué)報(bào):自然科學(xué)版,2000,21(2):161-163.

[8] 董軍.H形壓彎構(gòu)件截面設(shè)計(jì)快速優(yōu)化方法[J].建筑結(jié)構(gòu),1995(5):18-22.

[9] 黃冀卓,王湛,龔明袖.遺傳算法在鋼結(jié)構(gòu)截面優(yōu)化設(shè)計(jì)中的應(yīng)用[J].四川建筑科學(xué)研究,2005,31(3):26-30.

[10] Eberhart R C,Kennedy J.A New Optimizer Using Particle Swarm Theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya,Japan,Piscataway,NJ:IEEE Service Center,1995:39-43.

[11] Sun J,Feng B,Xu W B.Particle Swarm Optim ization with Particles Having Quantum Behavior[C]//Proceedings of 2004 Congress on Evolution Computation.Piscataway,NJ:IEEEPress,2004:325-331.

[12] 王勇,蔡自興,周育人,等.約束進(jìn)化優(yōu)化算法[J].軟件學(xué)報(bào),2009,20(1):11-29.

[13] Sun J,Feng B,Xu W B.A Global Search Strategy of Quantum-behaved Particle Swarm Optimization[C]//Proceedings of IEEE Conference on Cybernetics and Intelligent Systems.Piscataway,NJ:IEEE Press,2008:111-116.

[14] 夏志斌,姚諫.鋼結(jié)構(gòu)設(shè)計(jì)例題集[M].北京:中國建筑工業(yè)出版社,1994.

[15] 中華人民共和國建設(shè)部.GB50017—2003鋼結(jié)構(gòu)設(shè)計(jì)規(guī)范[S].北京:中國建筑工業(yè)出版社,2003.

[16] 魏明鐘.鋼結(jié)構(gòu)[M].武漢:武漢理工大學(xué)出版社,2005.