基于二次分形插值函數的分形插值曲面的變差與盒維數

黃艷麗,馮志剛

(江蘇大學理學院,江蘇鎮江 212013)

0 前言

分形插值曲面是分形幾何理論中的一個重要內容,在圖形與圖像處理、材料科學、地理地質科學及計算機動畫仿真等領域具有廣泛的應用。

在矩形區域中,一般通過構造二元迭代函數系生成分形插值曲面[1-3],但有嚴格的限制條件。文獻[4]給出了矩形區域上分形插值曲面更加一般的連續性條件,但這一條件也過于苛刻,且在實際應用中不易判別。文獻[5]中應用一元遞歸分形插值函數生成分形插值曲面,并給出了這類插值曲面盒維數的一個下界估計,這種方法解除了邊界插值結點共線和壓縮因子相等的限制條件,使得分形插值更具靈活性,更有利于實際應用。

本文研究了由二次分形插值函數生成的分形插值曲面的變差與盒維數。第 1節介紹了基于二次插值函數的分形插值曲面的構造方法;第 2節給出了連續函數中心變差的概念,以及連續函數圖像的盒維數的計算公式;第 3節研究了分形插值函數的中心變差的性質,對分形插值曲面的的中心變差進行了估計,并利用二元連續函數的中心變差與其圖像計盒維數之間的關系,得到了分形插值曲面的計盒維數。

1 基于二次分形插值函數的分形插值曲面的構造

設I=[0,1],J=[0,1],△={(xi,yj,zij):i=0,1,…,N;j=0,1,…,M}為I×J上的插值結點,其中,0=x0＜x1＜…＜xN=1;0=y0＜y1＜…＜yM=1。記Ii=[xi-1,xi],Jj=[yj-1,yj]和K= J×R。對于i=0,1,2,…,N,假設ui(y),y∈J,分別是過插值結點△xi={(xi,yj,zij):j=0,1,2,…,M}的一組連續函數。現給定壓縮因子集S={s1,s2,…,sN},其中,＜1,i=1,2,…,N。

固定y∈J,對于i=1,2,…,N,令Fy,i(x,z)=siz+by,ix2+cy,i滿足條件:

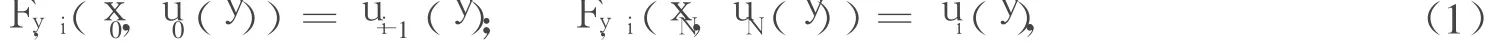
定義映射wy,i:K→K,

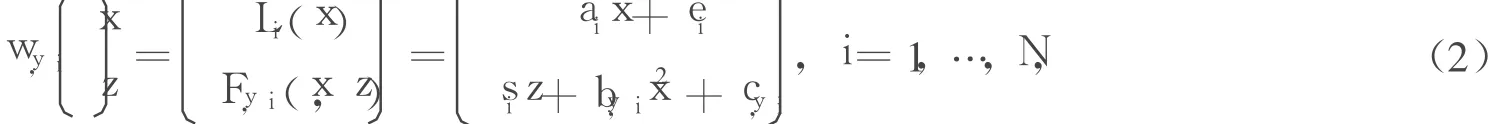
其中,ai=xi-xi-1;ei=xi-1。由條件(1)可得:

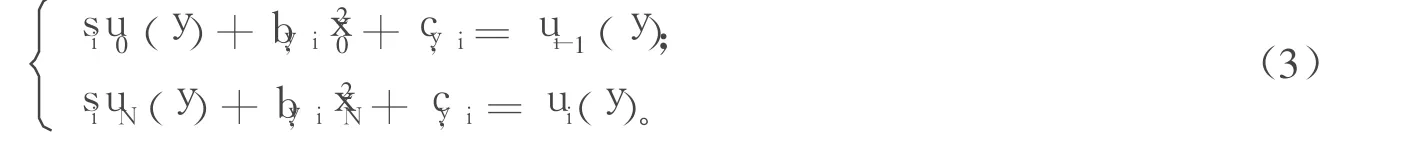
易證 wy,i在此度量下是壓縮映射。則由文獻[6]可得下面的定理。

定理1 對y∈J=[0,1],{K,wy,i,i=1,2,…,N}構成雙曲迭代函數系,且存在I上的連續函數fy,使得fy的圖像Γ(fy)={(x,fy(x))}是迭代函數系{K,wy,i,i=1,2,…,N}的不變集,即Γ=∪wy,i(Γ),并且fy(xi)=ui(y),i=1,2,…,N,稱fy是對應于{K,wy,i,i=1,2,…,N}的二次分形插值函數。

定義函數F:[0,1]×[0,1]→R,使得F(x,y)=fy(x)。 (4)

引理1[7]設fy、fy′分別為過插值集△y={(xi,y,ui(y)):i=0,1,…,N},△y′={(xi,y′, ui(y′)):i=0,1,…,N}的分形插值函數,且有相同的壓縮因子S={s1,s2,…,sN},則:

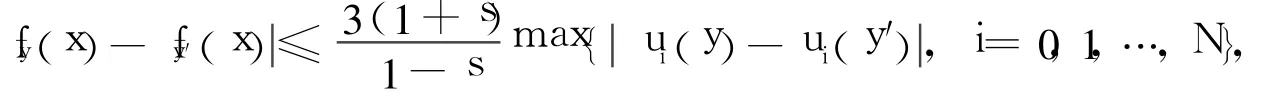
引理2 F為式(4)定義的二元連續函數,則F連續。

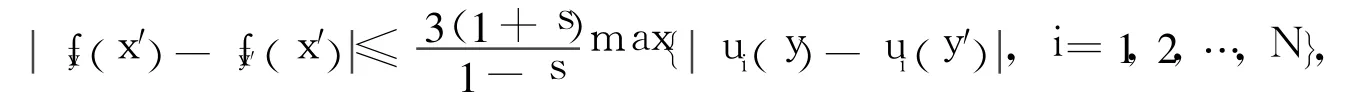
又ui連續,則＜δ2時,?ε＞0, max{＜) ε。所以,

2 連續函數的中心變差與計盒維數公式

連續函數的變差是量化函數圖像粗糙性質的一個重要參數,對于變差的性質及它與分形維數的關系有了較多的研究,參見文獻[8-9]。為了方便以后的研究,下面給出中心振幅與中心變差的定義。

設D={ξ=(ξ1,ξ2,…,ξn):ai≤ξi≤bi,i=1,2,…,n}?Rn,任給ξ∈D,令

D[ξ;δ1,δ2,…,δn]=D∩([ξ1-δ1,ξ1+δ1]×[ξ2-δ2,ξ2+δ2]×…×[ξn-δn,ξn+δn])。

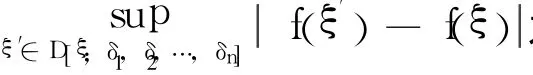
由振幅的定義,顯然振幅與中心振幅有下面關系:

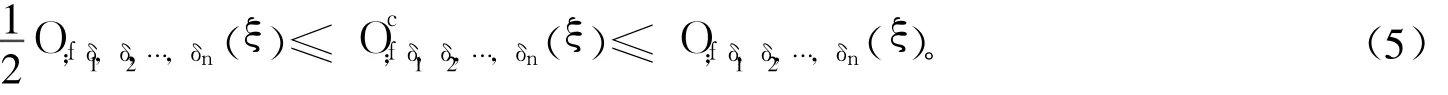
容易得到計盒維數與中心變差的關系。

定理2 設Γ(f,D)是連續函數f的圖像,則:

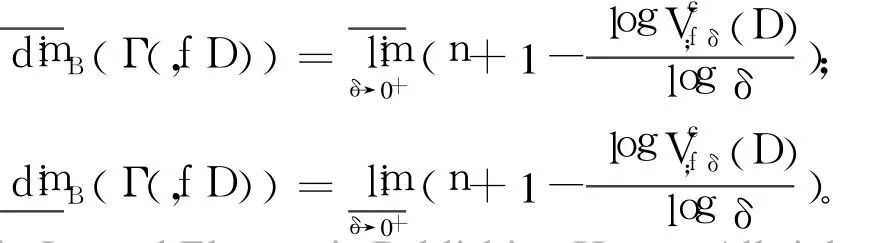
3 二元分形插值函數的中心變差與計盒維數

引理3 設fy是定理1確定的分形插值函數,則(I)在J上關于y連續。

證明 Γ={fy:y∈J}?C([0,1])在＜C[0,1],∞＞上緊,則 Γ等度連續,即對每一x0∈I, ε＞0,?δ＞0,若＜δ,對?y∈J,

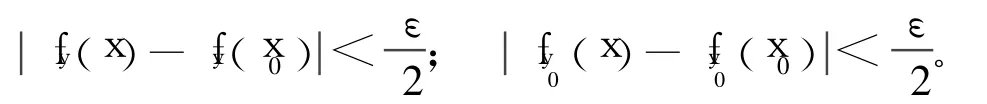
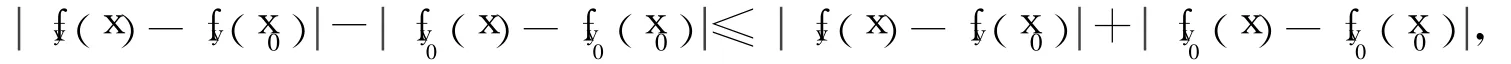
引理4 若對于某一yc∈J,插值結點{xi,ui(yc),i=0,1,…,N}不共線,則存在閉區間[a,b]?J,對于任意y∈[a,b],插值結點{xi,ui(y),i=0,1,…,N}均不共線。

證明 因為{xi,ui(yc),i=0,1,…,N}不共線,存在i0∈{1,…,N-1},使得h(yc)≠0,其中, h(y)=ui0(y)-[u0(y)+(uN(y)-u0(y))xi0]。由于ui0(y)、u0(y)和uN(y)均為區間J上的連續函數,從而h(y)在J上也連續。因此,存在閉區間[a,b]?J,對于任意y∈[a,b],函數h(y)≠0。所以,當y∈[a,b]時,點集{xi,ui(y),i=0,1,…,N}均不共線。引理證畢。

定理3 F是由式(4)定義的二元連續函數,對于任意0≤a＜b≤1有:

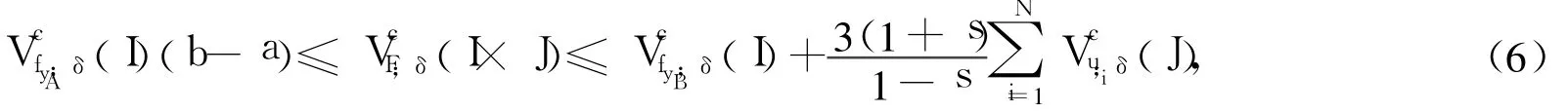
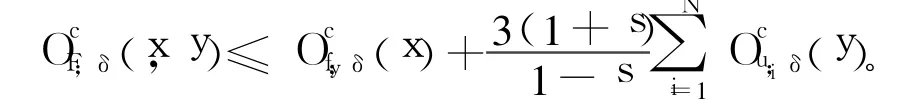
則:

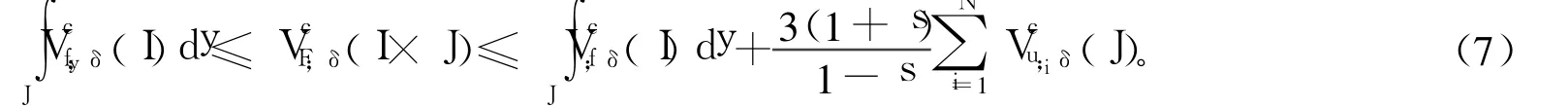
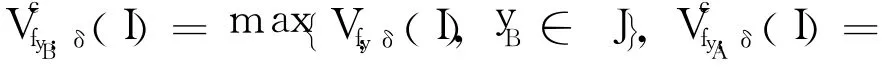
定理4 F∶[0,1]×[0,1]→R是連續函數,Γ(F,D)是它的圖像,設max dimB(fy)=d1,y∈J, max{dimB(ui),i=1,2,…,N}=d2且d1≥d2,則:

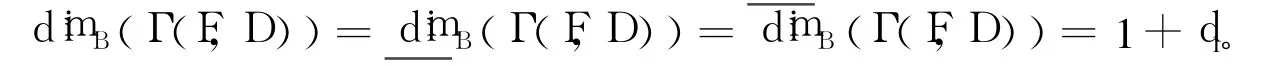
再由定理2和定理3得:

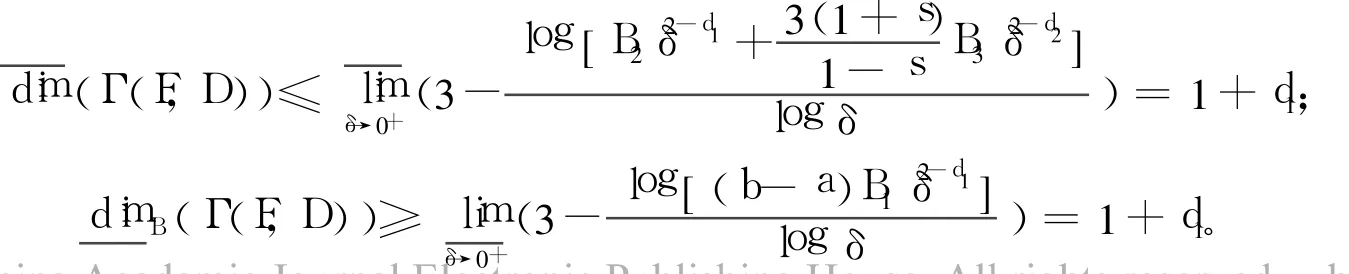
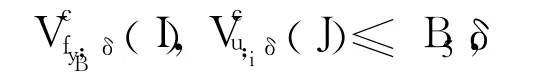
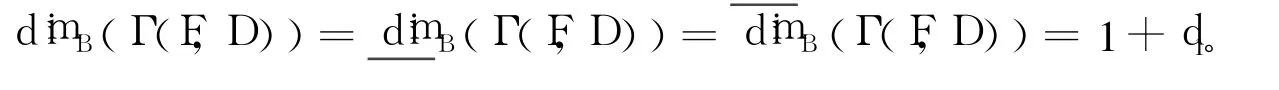
[1] Robert M.The MinkowskiDimension of the Bivartiate Fractal Interpolation Surfaces[J].Chaos,Solition and Fractal,2006, 27:1147-1156.

[2] 徐惠,馮志剛.一類分形插值函數的變差和計盒維數[J].安徽工業大學學報,2008,25(4):444-447.

[3] 江镅,馮志剛.一類多參數分形插值曲面[J].成都信息工程學院學報,2009,24(6):616-618.

[4] Feng Zhigang.Variation and Minkowski Dimension of Fractal Interpolation Surface[J].Journal of Mathematical Analysis and App lication,2008,345(1):322-334.

[5] Bouboulis P,Dalla L.Fractal Interpolation Surfaces Derived from Fractal Interpolation Functions[J].JournalofMathematical Analysis and App lication,2007,336:919-936.

[6] 沙震,阮火軍.分形與擬合[M].杭州:浙江大學出版社,2005.

[7] Feng Z,Xie H.On Stability of Fractal Interpolation[J].Fractals,1998,6(3):269-273.

[8] 文志英.分形幾何的數學基礎[M].上海:上海科學技術出版社,2000.

[9] 馮志剛,王磊.分形插值函數的δ-變差的性質[J].江蘇大學學報:自然科學版,2005,26(1):49-52.