半連續函數的預不變凸性

王海英,武慧虹

(安順學院數學與計算機科學系,貴州安順 561000)

0 前言

凸性理論(包括凸集理論和凸函數理論)在數理經濟學、對策論、工程、管理科學和最優化理論中起著非常重要的作用,這主要是因為凸函數在凸集上的局部極值也一定是其全局極值。事實上,具有凸性的函數相對來說是很少的。因此,人們一直在研究凸函數的各種推廣形式即廣義凸函數,使其既能保持凸函數的一些良好性質又具有比凸性更弱的條件。20世紀 80年代以來,國內外學者對廣義凸函數的研究興趣與日俱增,他們多方位、多角度、多途徑地對廣義凸函數的條件、結論進行廣泛地拓展,取得了一系列研究成果[1-9]。1988年,文獻[1-2]引入了不變凸集和預不變凸函數的定義,研究了它的性質及其在優化理論中的應用。2001年,文獻[3]得到了預不變凸函數的若干性質。文獻[4]根據條件 C得到了條件C′,并且討論了條件C與條件C′的關系。

本文在此基礎上對預不變凸函數作了進一步研究,在排除文獻[3]中 X是開集及集合 A={λ∈[0, 1]:f(y+λη(x,y))≤λf(x)+(1-λ)f(y),?x,y∈X}在[0,1]中的稠密性條件下,而得到了相同的結論,從而簡化了一些預不變凸函數性質定理的證明。

1 預備知識

定義1 設X?Rn,如果存在一個向量函數η:Rn×Rn→Rn,使得?x,y∈Rn;?λ∈[0,1]有y+λη(x,y)∈X,則稱集合X關于η是不變凸集。

定義2 設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,實值函數f:X→R,若?x,y∈Rn;?λ∈[0,1]有f(y+λη(x,y))≤λf(x)+(1-λ)f(y),則稱f關于相同的η是預不變凸函數。

定義3 設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,實值函數f:X→R,若?x,y∈Rn,?λ∈[0,1],當x≠y時,有f(y+λη(x,y))＜λf(x)+(1-λ)f(y),則稱f關于相同的η是嚴格預不變凸函數。

條件C:稱向量函數η:Rn×Rn→Rn滿足條件C,如果?x,y∈Rn;?λ∈[0,1]有:

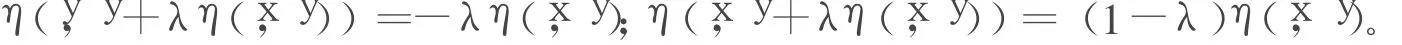
條件C′:稱向量函數η:Rn×Rn→Rn滿足條件C′,如果?x,y∈Rn;?λ1,λ2∈[0,1]有:

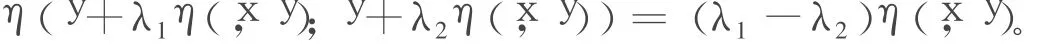
條件D:設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,稱實值函數f:X→R滿足條件D,若?x,y∈X,有f(y+η(x,y))≤f(x)。

條件H:如果λn∈[0,1],且λn→λ,則對 ?ε＞0,?正整數N,當n＞N時,對?x,y∈X都有f(y+η(x,y))≤f(y+λnη(x,y))+ε。

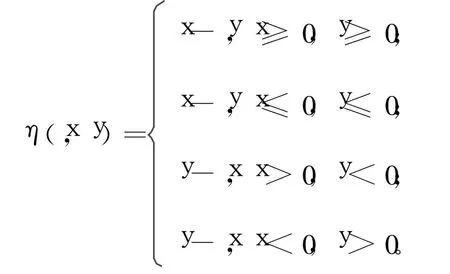
由文獻[5]可知:f是關于η的預不變凸函數。

引理1 設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,η滿足條件C,則η滿足條件C′。

引理2 設X?Rn是緊集,實值函數f:X→R上半連續,則f在X上取得最大值。

2 主要結果

定理1 設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,實值函數f:X→R,若f上半連續且滿足條件D,η滿足條件C′,則f關于相同的η是預不變凸函數??α∈(0,1)對?x,y∈X,有f(y +αη(x,y))≤αf(x)+(1-α)f(y)。

證明 必要性顯然。下證充分性。

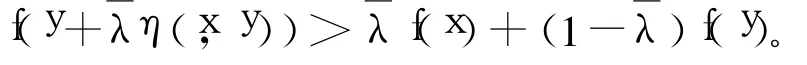
令:

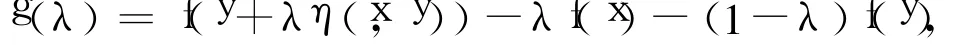
因f上半連續,則g(λ)在[0,1]上也上半連續,從而由引理 2知:g(λ)在[0,1]上存在最大值 M0。

令:

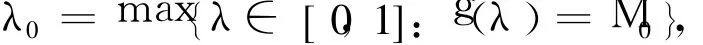
易知g(0)=0,由f滿足條件D可知:g(1)=f(y+η(x,y))-f(x)≤0,因而λ0∈[0,1]。

選取δ,使得

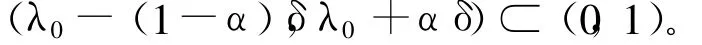
令:

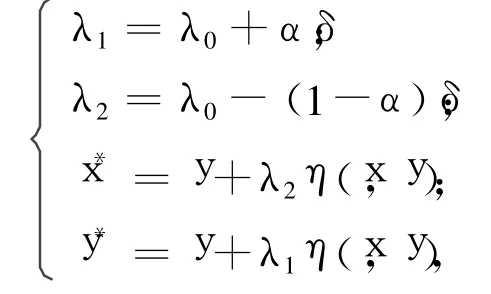
則由η滿足條件C′得:

從而由題設條件有:

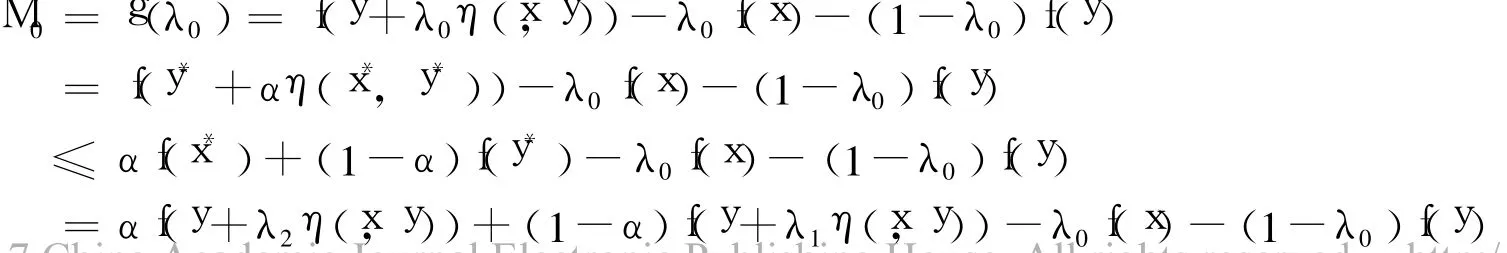
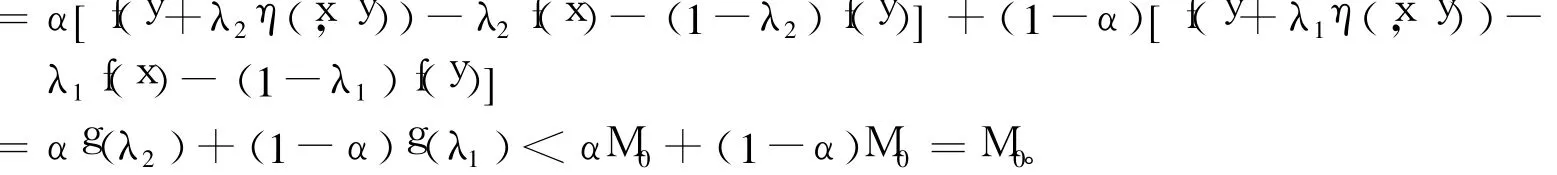
矛盾,故假設不成立,即 f關于相同的 η是預不變凸函數。

定理2 設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,實值函數f:X→R,若f下半連續,則f關于相同的η是預不變凸函數??α∈(0,1)對?x,y∈X,有f(y+αη(x,y))≤αf(x)+(1-α)f(y)。

證明 必要性顯然。下證充分性。令:

如果λn∈A,且λn→λ,則由A的定義,對?x,y∈X,有:

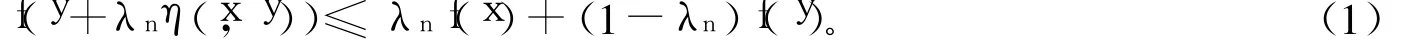
又f下半連續,則f滿足條件H,則對?ε＞0,?正整數N,當n＞N時,對?x,y∈X都有:

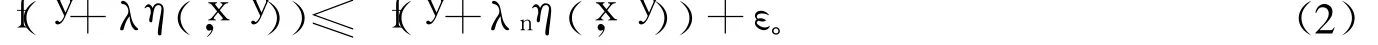
由式(1)、式(2)可得:

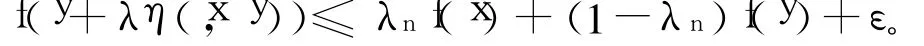
由λn→λ和ε的任意性,有:

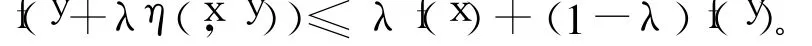
從而f關于相同的 η是預不變凸函數。

3 預不變凸函數在數學規劃問題中的應用

設對于x∈X的求f(x)的最小值的數學規劃問題為(P):

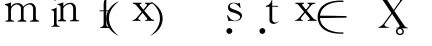
定理3 設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,實值函數f:X→R關于相同的η是嚴格預不變凸函數,如果是關于規劃問題(P)的局部最優點,則一定是關于規劃問題(P)的全局唯一的最優點。

假設x不 是規劃問題(P)的全局最優點,則必存在∧x∈X,使得:

因為f:X→R關于相同的η是嚴格預不變凸函數,故對于?λ∈[0,1]有:

當λ充分小時,有:

(Ⅱ)唯一性。假設x0,x1∈X為規劃問題(P)的兩相異全局最優點,則f(x0)=f(x1)。由于X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,則對于?λ∈[0,1]有x0+λη(x1,x0)∈X。因為f:X→R關于相同的 η是嚴格預不變凸函數,故:

這與x0是關于規劃問題(P)的全局最優點矛盾,故規劃問題(P)的全局最優點唯一。

綜上可知:x0是關于規劃問題(P)的全局唯一的最優點。

定理4 設X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,實值函數f:X→R關于相同的η是預不變凸函數,則規劃問題(P)的最優解集是不變凸集。

證明 設x,y是規劃問題(P)的解,由于X?Rn是關于向量函數η:Rn×Rn→Rn的不變凸集,則對于?λ∈[0,1],有z=y+λη(x,y)∈X。因為f:X→R關于相同的η是預不變凸函數,故:

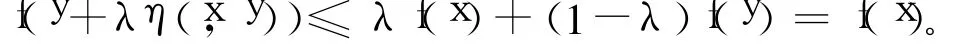
即z=y+λη(x,y)也是規劃問題(P)的最優解,因而規劃問題(P)的最優解集是不變凸集。

注:定理3、定理4一方面可以看作是預不變凸函數的兩個很好的性質,同時也表明預不變凸函數在數學規劃中有著非常重要的意義和地位。

[1] Weir T,Mond B.Prieinvex Functions in MultipleObjective Optim ization[J].JournalofMath Analand Appl,1988,136:29-38.

[2] Weir T,Jeyakwmar V.A Class of Nonconvex Functions and Mathematical Programming[J].Bulletin of Australian Mathematical Society,1988,38:177-189.

[3] Yang X M,Li D.On Properties of Preinvex Function[J].Journal of Optim ization Theory Applications,2001,256:229-241.

[4] 雙立青.多目標規劃在廣義凸性下的最優化條件的研究[D].武漢:武漢科技大學,2007.

[5] 彭建文.廣義凸性及其在最優化問題中的應用[D].呼和浩特:內蒙古大學,2005.

[6] Mohan SR,Neogy SK.On Invex Sets and Preinvex Function[J].Journalof Math Analand App l,1985,189:902-908.

[7] 楊新民.上半連續函數的擬凸性[J].運籌學報,1999,3(1):48-51.

[8] 韋麗蘭.預擬不變凸函數與半連續函數的關系[J].江西師范大學學報:自然科學版,2009,33(2):242-244.

[9] 彭再云,林志,劉亞威.E-擬凸函數的新性質及應用[J].河北大學學報:自然科學版,2009,29(6):564-566.