貨幣供給和就業的協整檢驗及影響分析

龔璨詩(武漢理工大學管理學院，湖北 武漢430070）

李 靜，黎東升(長江大學經濟學院，湖北 荊州434025）

在全球金融危機中，中國采取了擴張性的貨幣政策，所以銀行系統的流動性供給增加。2010年《中國統計年鑒》的數據顯示，截至2009年底，廣義貨幣供給增加了27．7%，狹義貨幣供應增加了32．4%，在過去的15a中達到了最高的水平[1]。

貨幣數量理論認為，每一次通貨膨脹的背后都有貨幣供給的迅速增長[2]。因此，巨額的貨幣投放引發價格水平上漲的壓力。從經濟理論可知，通貨膨脹和就業(失業）是短期宏觀經濟運行中2個主要問題，按照短期菲利普斯曲線，通貨膨脹率和失業存在替換關系，即通貨膨脹率增加，失業率降低，反之，通貨膨脹率降低，失業率就增加。對應就業的關系，則通貨膨脹率增加，就業就增加，通貨膨脹率降低就業率就降低。如果說通貨膨脹是由貨幣供給引起的，那么研究通貨膨脹與就業的關系就轉化為研究貨幣供給與就業的關系。同時，如果菲利普斯曲線所表示的通貨膨脹率和失業存在替換關系成立的話，那么貨幣供給與就業的均衡性也應該成立。如果這種均衡不成立的話，則肯定有外部因素沖擊影響[3]。因此，可以通過研究貨幣供給與就業的均衡性來反映外部沖擊對就業的變動影響，從側面反映我國就業變動的原因。

1 貨幣供應和就業之間的協整檢驗

在理論上，貨幣供給和就業之間存在一個長期穩定的關系。然而，隨著經濟活動的復雜性，貨幣供應和就業之間可能存在著短期的失衡，因此，有必要檢測一下貨幣供給和就業之間的關系。通過定義協整變量，本研究將檢驗協整變量是否有單位根來說明變量間的協整性，用變化率作為協整變量，貨幣供給采用廣義的貨幣供給（M2），首先i產業的就業被定義為Eit，新的協變量定義為Vit=M2t／Eit，如果協整變量是平穩時間序列，那么貨幣供給（M2）與i個產業的就業是協整的。為此，這里使用ADF單位根檢驗來判斷數據生成的過程。對于ADF單位根檢驗，采用如下方程：

ADF單位根檢驗首先根據數據表現的特征來選擇適當的模型。即無論模型（1）是否包含了截距項和趨勢項，這都采用T-檢驗。同時，模型（1）要選擇一個適合的滯后階數。滯后項階數的選擇是一個關鍵，合適的滯后階數應是殘差呈現獨立同分布結構，可以采用最小信息標準進行檢測。

這里首先用V1=M2t／E1說明檢測過程。依據模型（1），滯后項應該從0開始，逐步1階、2階依次遞增。最小信息準則是選擇的標準。如果合適的滯后項是2，則模型的估計結果為：

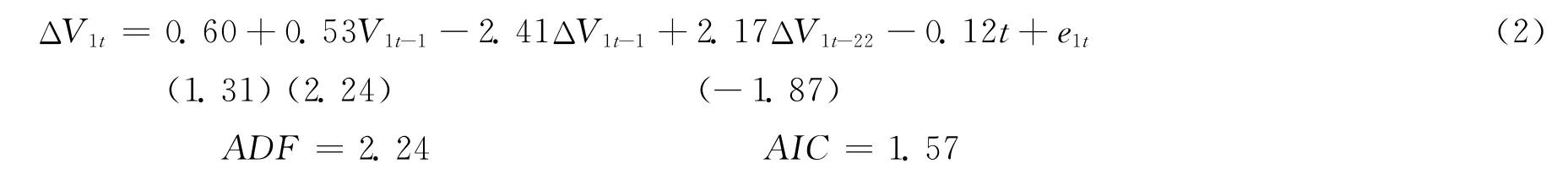
模型（2）的顯著性檢驗是，原假設：α（α=0．60）=0，β（β=-0．12）=0，ast（α）=1．31，P=0．19＞0．05，因此，在5% 的顯著性水平下不能拒絕原假設，即模型（2）沒有截距項。同理，t（β）=-1．87，P=0．08＞0．05，因此，在5%的顯著性水平下亦不能拒絕原假設，即模型（2）沒有趨勢項。因此，對應的估計式為：

由于ADF（0．987）大于顯著性水平為0．005的臨界值-1．958，因此接受單位根的原假設。選擇合適的滯后項對結論是非常重要的，因此，模型階數應該從0開始逐步選取，如果選擇1階，估計結果是：

由于AIC（1．65），大于模型（2）的最小信息準則（AIC=1．57），因此不能選擇模型（4）。如果滯后階數為3，估計結果為：

根據模型（5）可以看出，此時的AIC=1．65，也大于模型（2）的最小信息準則（AIC=1．57），與此同時β3=0．95，t=0．72時不顯著。依次增加滯后階數并進行比較，比較結果為模型（3）是最佳選擇模型。

對于模型（3），最終的結論是V1是單位根變量，即V1～I（1）。根據V1的定義，可以知道V1是貨幣供給量（M2）和第一個產業的就業量（E1）之比，而V1是單位根，表明V1是非平穩時間序列。因此，貨幣供給量（M2）和的第一個產業就業（E1）之間不協整，兩者之間不存在長期均衡關系。基于以上的分析，下面繼續檢驗單位根V2、V3的情況，測試結果見表1。

表1 單位根檢驗

從表1可以看出，V1是沒有時間趨勢、沒有截距的2階單位根信息，V2是隨機過程，V3是沒有時間趨勢、沒有截距的1階單位根過程生成。因此，3個變量都是很平穩的。

根據上述過程可知，貨幣供給之間（M2）和第一產業、第二產業和第三產業的就業之間都是非協整的，所以不存在長期均衡關系。因此，貨幣供給量和各個產業的就業存在非協整性，沒有長期穩定的關系。正是這種非協整性暗示了貨幣供給增加不能長期均衡地引起就業的增加，一定存在非貨幣因素對這種均衡的沖擊。

2 影響貨幣供應和就業穩定性的外部沖擊因素

基于以上分析，貨幣供給和各產業的就業是一個非穩定系統，那么肯定存在非貨幣供給效應的其他影響因素。由于系統的穩定性可以通過函數的系統穩定性給予反映，因此，可使用隨機變量參數模型來進行實證分析。如Hildreth-Houck模型所示：

模型（6）主要體現的是結構參數非穩定性。從模型（6）可以看出，隨機參數影響了參數的穩定性。如果單獨分析貨幣供給對就業的影響及隨機因素的沖擊效應，則模型（6）可以改變成以下的形式：

其中，αt=α0＋εt，βt=β0＋ηt，Var（εt）=Var（ηt）=σj2=Var（μt）=σ2

則：

對模型（8）的隨機部分進行描述：

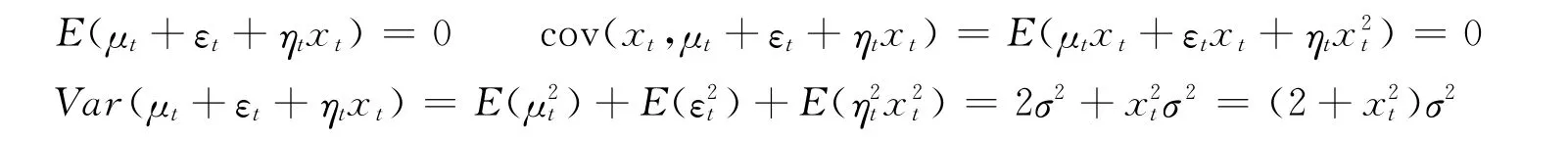
因此，模型（8）存在異方差，需要采用加權最小二乘法來估計。

如果不考慮貨幣供給之外的隨機因素的影響，那么研究貨幣供給對就業的效應的模型選擇就可以用一般的雙變量線性回歸模型，而這種模型應滿足經典假定。雙變量線性回歸模型的結構參數保持不變，它衡量了自變量對因變量的穩定關系。下面是隨機變參數Hildreth-Houck模型和雙變量線性回歸模型估計的結果并進行比較，通過比較分析可以體現隨機因素對就業的沖擊情況。

表2 估計結果

從表2可以看出，隨機變參數Hildreth-Houck模型和雙變量線性回歸模型有不同的截距和斜率，如果單獨考慮貨幣供給對第一、第二及第三產業就業的引致效應，那么隨機因素對就業的沖擊效應就可以比較隨機變參數模型和雙變量線性回歸模型的斜率大小。根據表2的Ⅰ、Ⅱ、Ⅲ的回歸方程來看，隨機變參數模型的斜率大于雙變量線性模型的斜率。這表明，隨機因素影響了貨幣供給對第一、第二及第三產業的就業效應，也就是說貨幣供給對就業的效應受到貨幣供給之外隨機因素沖擊的影響。正是這種影響造成貨幣供給與各個產業就業非協整性。同時表2也表明，由于隨機變參數模型的斜率大于雙變量線性模型的斜率，因此這種隨機沖擊帶來正效應。之所以出現隨機沖擊的正效應，其原因在于隨機因素所包含的內容。這里特別強調的是，本研究所指的隨機因素包含除貨幣供給之外的所有影響就業的因素，比如GDP增長率、經濟結構狀況、政府的宏觀調控、財政政策以及全球性經濟危機等等，這些因素有的促進就業的增長，有的則使就業減少，因此，對于雙變量線性回歸模型是在不考慮外在隨機因素的情況下回歸的結果，而隨機變參數Hildreth-Houck模型則考慮到外在隨機因素的沖擊情況，由于隨機變參數模型所回歸方程的斜率大于雙變量線性模型回歸的斜率，所以，這種外在隨機因素帶來的沖擊具有正效應。

3 主要結論

綜上所述，雙變量線性回歸模型的結果表明，貨幣供應量對第一產業就業的影響不顯著(t=-1．61），但貨幣供應量對其他兩個產業就業的影響是顯著的，因此貨幣供給影響就業：貨幣供給增加，就業增加。如果貨幣供給的增加導致通貨膨脹，那么菲利普斯曲線所表達的替代關系得到了證實。然而，按照以上的單位根檢驗，貨幣供給和三次產業的就業之間非協整，所以他們不存在長期穩定的關系，而這種不穩定性主要是由于其他變量導致的，而不是由貨幣供給造成的。

[1]中華人民共和國國家統計局 ．中國統計年鑒·2010[M]．北京：中國統計出版社，2010．

[2]Masanori Hashimoto．Investment in Employment Relations in Japanese Firms [J]．Journal of the Japanese and International Economic，1995，16：75-95．

[3]Yu-Fu Chen and Michael Funke．Product market competition，investment and employment-abundant versusjob-poor growth：A real options PersPeetive [J]．European Journal of Political Economy，2007，21：56-70．