考慮電壓穩定約束的電力系統無功規劃

程浩忠,顧穎中,熊 寧

(上海交通大學電氣工程系,上海 200240)

1 引言

無功規劃與傳統的無功優化不同。無功優化RPO(Reactive Pow erOptim ization)是在系統現有的無功補償元件及調節設備范圍內,在滿足系統各項約束條件下,使系統運行費用(通常是使網絡損耗)最小。而無功規劃RPP(Reactive Pow er Programming)是為達到某種目標(通常是使系統靜態電壓穩定裕度高于某個閥值)而對需投入無功備用設備進行規劃的問題。

常規無功規劃問題的求解方法,主要有試驗誤差法、非線性規劃法、動態規劃法、智能進化算法以及線性規劃法[1,2]。其中,內點法以其計算效率的高效性和對約束處理的方便性得到了廣泛的應用。Karm arkar在1984年提出內點法后[3],許多學者對其進行了擴展研究,相繼提出了一些完善方法,并在電力系統中得到了廣泛地應用,如將對數壁壘函數與牛頓法結合起來應用到非線性規劃問題[4,5]中等。在內點法的基礎上,M ehrotra提出了基于預測校正的原對偶內點法[6],由于該方法在計算中引入預測、校正環節,故可以計及互補松弛條件的二次性和動態地確定向心參數的取值,從而能夠較好地協調解的最優性及可行性之間的關系,改善算法的收斂性能。

2 負荷裕度指標的定義

負荷裕度指標是評估電力系統靜態電壓穩定性的有效手段之一。它是指從系統當前運行點到電壓崩潰點的“負荷距離”,具有較好的線性和直觀性。它可以使運行人員清晰地了解系統目前所處的狀態,并提前采取有效措施避免電壓崩潰的發生。

如圖1所示的P-U曲線,當前系統的運行點是PL0,即表示當前系統的負荷。Pcr對應著系統電壓崩潰的臨界點,即代表系統所能承受的極限負荷量。Pcr-PL0即為該系統的靜態電壓穩定負荷裕度。由此可以定義系統的相對負荷裕度λ為:

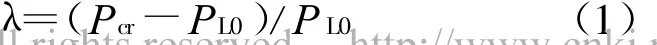
由P-U曲線可以看出,當系統的負荷裕度較大時,系統的電壓水平也較高;同樣,當系統接近電壓崩潰臨界點時,系統裕度很小,系統電壓水平也相應下降。利用此電壓穩定評價指標,可以清晰地表示出系統電壓的穩定水平。

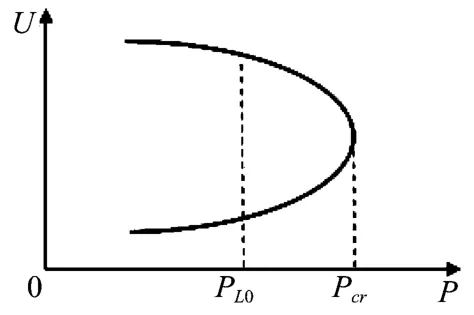
圖1 P-U曲線

3 無功規劃模型

以新增無功容量總和最小作為目標函數,無功規劃模型可用式(2)表示:

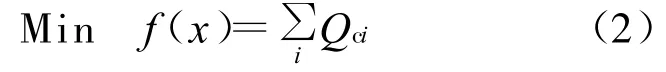
(1)等式約束方程h(x)

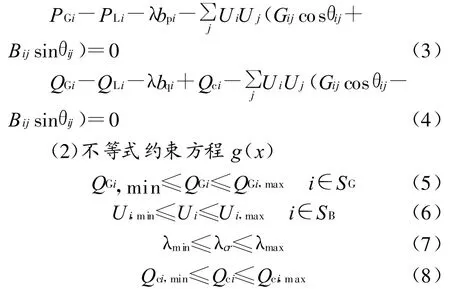
式中:Ui——節點 i的電壓幅值;θi——節點 i的相角; Bij——節點i與節點 j之間的互電納;Gij——節點 i與 j之間的互電導;Qc——補償容量;λcr——臨界點的負荷增量;Qci——節點i補償無功功率的容量;SB——所有節點的集合;bp——有功負荷增長方向;bq——無功負荷增長方向;SG——無功源集合;PGi——第i個節點發電機的有功;QGi——第i個節點發電機的無功;PLi——第i個節點負荷的有功;QLi——第i個節點負荷的無功;Qci——第i個節點的無功補償量。

4 模型的求解

采用預測-校正內點法對模型式(2)至式(8)進行求解,構造其拉格朗日函數,如式(9):

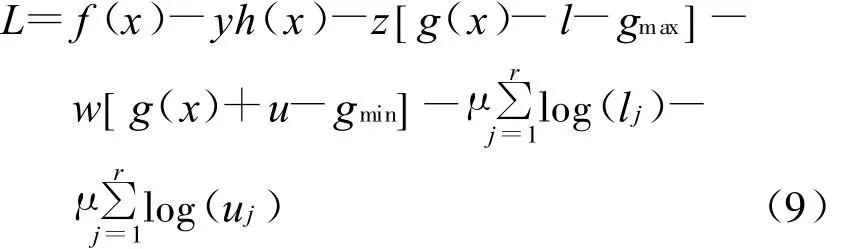
式(9)中,變量μ＞0為擾動因子(或稱障礙常數);l,u為松弛變量,且u＞0。

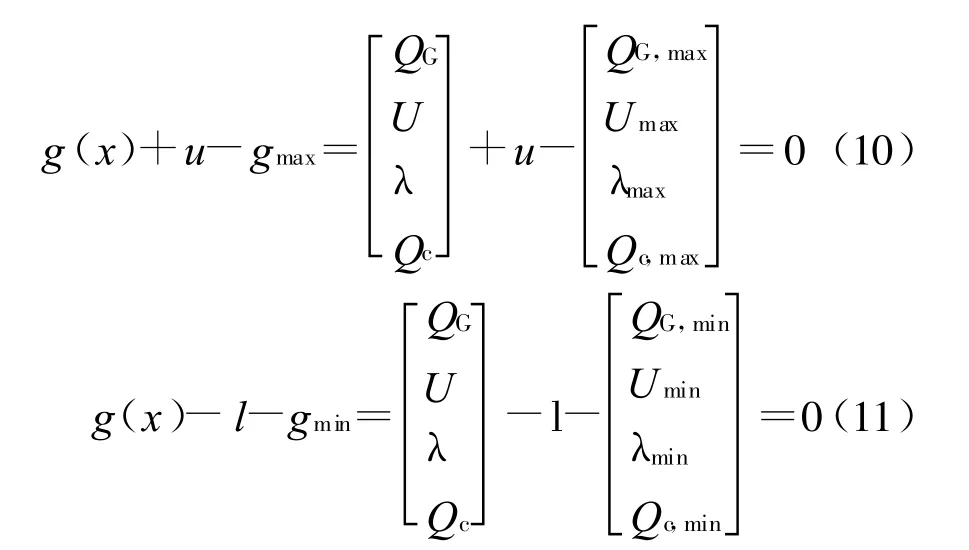
應用牛頓法得到待求問題的修正方程為:

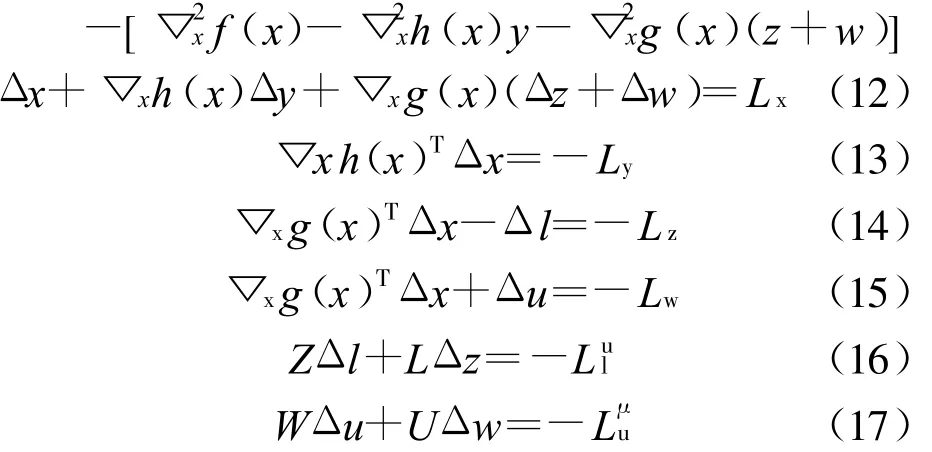
將式(12)至式(17)簡化后寫成矩陣,如式(18):

只需求解式(18)矩陣右下角分塊中的函數值,然后逐一回代,即可求出所有變量。求解方程組如式(19):

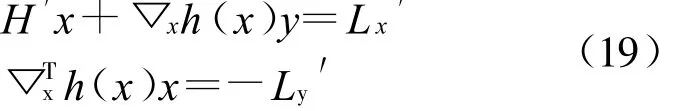
將所得解Δx,Δy回代到式(20),即可求出所有變量的解:

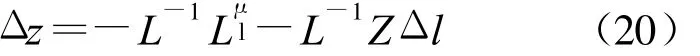
變量更新的迭代方程組為:

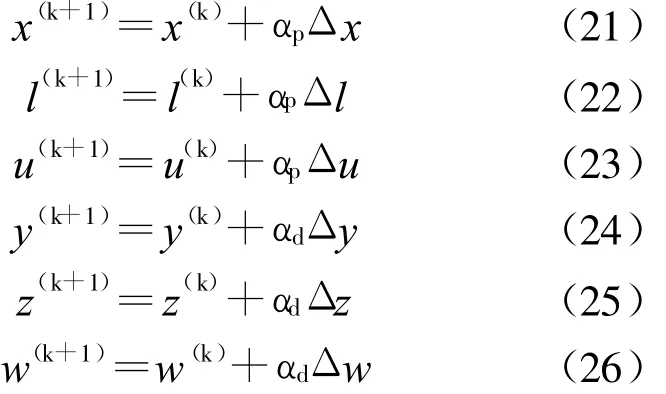
式中αd,αp分別為步長:

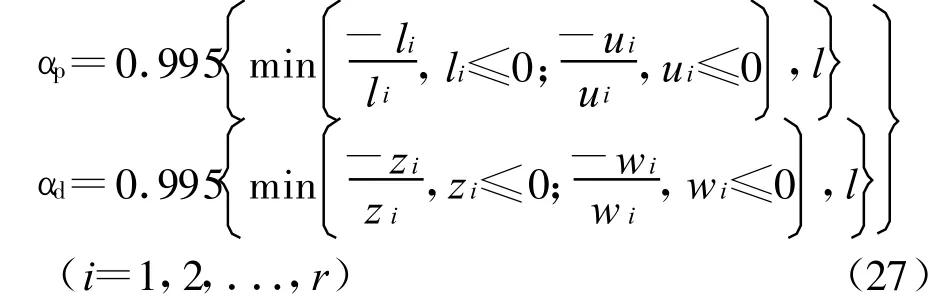
引入預測及校正環節動態確定向心參數的取值,并且利用互補松弛條件的二次性,預估計算結果,以較好地協調解的最優性及可行性之間的關系,改善算法的收斂性能。

(1)預測環節 對式(12)至式(17)的修正方程,取 μ=0,可求得 ΔxAff,ΔyAff,ΔzAff,ΔlAff, ΔuAff,ΔwAff。

式中:Aff表示仿射方向,即擾動因子取0時的牛頓方向。

根據預測過程,可確定仿射方向下的修正步長,如式(28)及相應的對偶間隙如式(29):

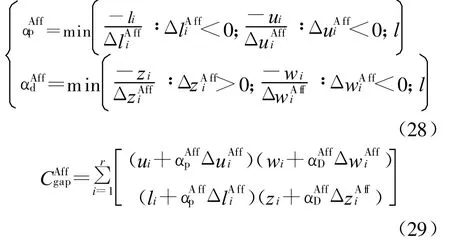
預測-校正原對偶內點法根據當前點的對偶間隙與仿射方向下的對偶間隙間的關系動態給定向心參數值,根據Mehrotra的經驗[6],σ一般為:

(2)校正環節 考慮到互補松弛條件式(16)及式(17)的二次性,將二次泰勒方程式展開,可表示為:

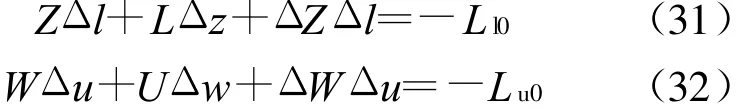
將 ΔZAff、ΔlAff、ΔWAff、ΔuAff分別代入,對ΔZΔl及ΔWΔu進行近似,對互補松弛條件進行校正,即:

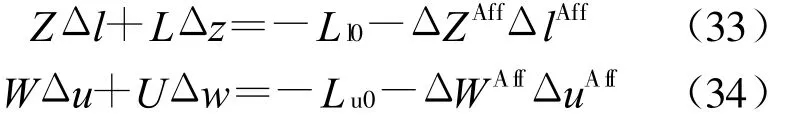
預測-校正原對偶內點法引入了預測-校正機制,充分利用了互補松弛條件的二次性,避開了向心參數的人為選取,同時也提高了收斂性。

5 IEEE標準算例仿真分析與應用

將無功規劃模型和求解方法用于IEEE 14、30、57、118標準算例,求解各系統初始負荷裕度結果如表1所示。其中,負荷增長方式設定為根據初始負荷大小全網同比例增長;發電機出力方式設定為系統中所有發電機(平衡機除外)根據各自有功備用的大小按比例分攤負荷的增量;優化目標為將系統原有的負荷裕度提升10%。

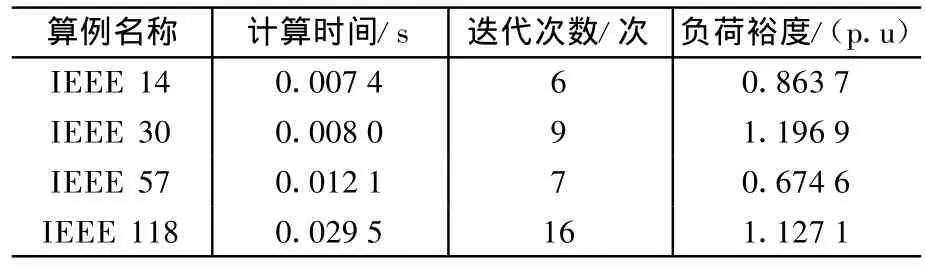
表1 IEEE標準算例負荷裕度求解結果

(1)IEEE 14節點無功補償方案為:10號節點的無功補償量為4.57 MW,13號節點的無功補償量為0.33 MW,14號節點的無功補償量為11.53MW,總計為16.43 MW。

(2)IEEE 30節點無功補償方案為:24號節點的無功補償量為3.85 MW,26號節點的無功補償量為4.22 MW,29號節點的無功補償量為1.01 MW,30號節點的無功補償量為6.28 MW,總計為15.36MW。

(3)IEEE 57節點無功補償方案為:30號的節點補償量為4.35 MW,33號節點補償量為2.91 MW,31號節點補償量為5.75 MW,總計為13.01MW。

(4)IEEE 118節點無功補償方案為:1號的節點補償量為28.28 MW,9號的節點補償量為86.67MW,總計為114.93MW。

上述無功補償量計算中所需時間隨節點數量的增多而線性增大,但是其增加的速率基本是多項式級的,由此證明內點法適合解算大規模系統問題。

利用上述無功規劃模型,在國內某個大型電力系統上驗證所提方法的有效性。負荷增長方式和發電機出力方式與上述定義相同,補償候選點集合為220 kV主變的低壓側節點,各節點無功補償下限為0,上限為主變容量的20%。

采用預測-校正原對偶內點法對該電網進行無功規劃,補償方案如表2所示。

如表2所示,該系統共有38個節點需要安裝無功補償設備,補償容量總計為354.05 MW。

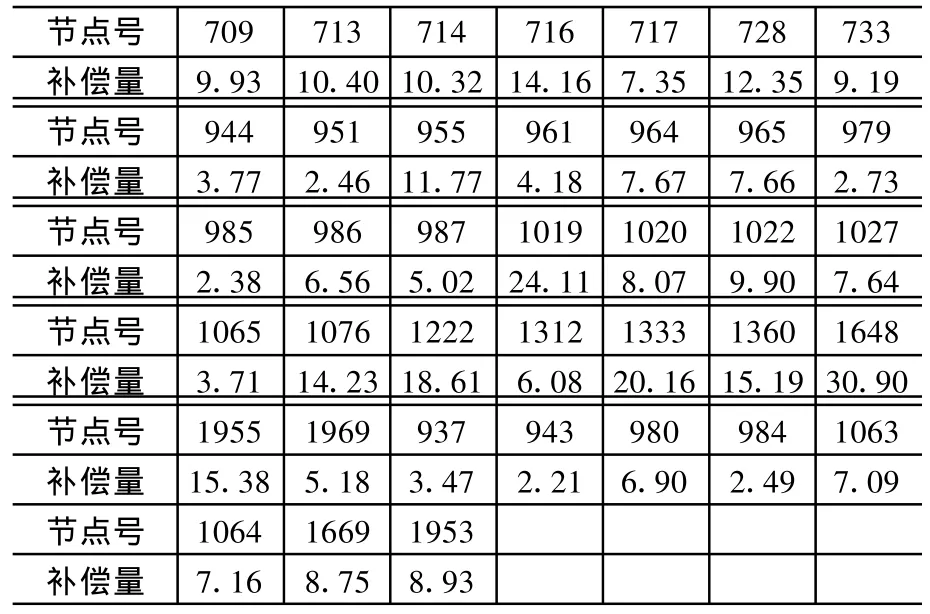
表2 國內某系統無功補償方案 MW

算法收斂過程如圖2所示。

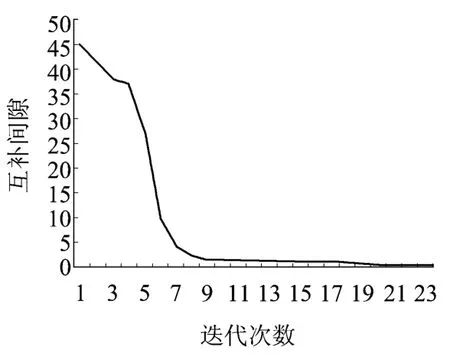
圖2 國內某電網無功規劃互補間隙收斂過程

預測-校正原對偶內點法經過27步迭代,耗時118 s收斂。在保證系統負荷裕度達到設定閥值的前提下,圓滿地完成了以補償量最小為目標的無功規劃。

6 結語

通過建立無功規劃的最優化模型,應用預測-校正原對偶內點法對其進行求解。在IEEE 14,IEEE 30,IEEE 57和IEEE 118系統和國內某個大型電網上,驗證了上述模型和求解方法的有效性。

[1] 文學鴻.基于內點優化算法的電力系統靜態電壓穩定分析與最優控制[碩士].河海大學,2007.

[2] 陳宏偉,張興凱,王 寬.電力系統無功優化的研究現狀和展望[J].電氣應用,2006(12).

[3] N.KARMARKAR.A new polynom ial-tim ealgorithm for linear programm ing[C],STOC'84 Proceedings of six teen th annual ACM symposium on Theory of computing,1984.

[4] 王錫凡.現代電力系統分析[M].北京:科學出版社,2003.

[5] 張伯明.高等電力網絡分析[M].北京:清華大學出版社,2007.

[6] S.MEHROTRA.On the Imp lementation of a Primal-Dual Interior Point Method[J],SIAM Jou rnal on Optim ization,Nov.1984.

[7] 劉沛津,谷立臣,韓行.基于內點法與改進遺傳法的無功規劃優化混合算法[J].電力系統保護與控制,2008(17).

[8] 鐘世霞,袁榮湘.內點法在電力系統中的應用述評[J].高電壓技術,2005(12).

[9] 文學鴻,袁 越,鞠 平.靜態電壓穩定負荷裕度分析方法比較[J].電力自動化設備,2008,28(5).

[10] 王佳賢,程浩忠,胡澤春.多負荷水平下的配電網無功優化規劃方法[J].電網技術,2008,(19).

[11] 吳 浩.電力系統電壓穩定研究[博士].浙江大學,2002.

[12] 韋 化,丁曉鶯.基于現代內點理論的電壓穩定臨界點算法[J].中國電機工程學報,2002,22(3):27-31.

[13] 程浩忠,吳浩著.電力系統無功與電壓穩定性[M].北京:中國電力出版社.2004.