氣動充放氣系統二維非定常流場數值模擬

朱冬，楊慶俊，包鋼

(哈爾濱工業大學 氣動技術中心，黑龍江 哈爾濱，150001)

隨著氣動系統在現代工業中越來越廣泛的應用，人們對氣動系統運行過程中壓縮空氣的狀態變化越來越關注[1-3]。系統內氣體狀態包括層流和湍流等多種形式，且氣體與系統元件、元件與外部空氣之間存在著非穩態傳熱[4]。同時，許多氣動元件的結構復雜，其內部流場的測量變得困難有時甚至不可能實現[5]，因此，對氣動流場進行數值計算就顯得尤為必要。許多學者對氣動系統流場進行了研究，如：李軍等[6]采用有限差分法對氣動充放氣系統進行了一維流場計算，對氣缸或容腔中的氣體采用集中參數法，將節流口進行等熵簡化處理；李玉軍等[7]將壓模型和壓力回復模型引入到一維流場中用來處理節流口邊界條件，計算得到的流場不能反映氣管、氣缸等元件的徑向參數分布以及節流口對管路流場的節流特性，難以滿足實際需要。楊麗紅[8]對固定容積容器的放氣過程進行了二維仿真研究，計算時考慮容器壁和內部氣體的傳熱，得到了放氣時放氣口的流場分布。本文作者建立了氣動充放氣系統的二維模型，考慮系統內氣體、元件和外部氣體之間的熱傳遞，采用湍流k-ε兩方程模型，運用有限體積法(FVM)和動網格技術[9-11]對充放氣過程進行了計算。將計算結果與試驗結果和絕熱模型計算結果進行對比，表明本方法與試驗結果具有較好的一致性，證明了本方法的正確性。這一方法可以用于計算出氣缸內部和節流口處的流場，為研究節流口節流特性及系統流場參數分布提供詳細的數據和參考。

1 氣動充放氣系統模型的建立

圖1所示為典型氣動回路。氣動回路包括氣源、電磁閥、管路、節流閥、氣缸和負載等。氣缸在換向閥的控制下進行充放氣。通過進氣回路向氣缸進氣腔充氣，通過放氣回路從氣缸放氣腔向系統外放氣。活塞未運動時，屬于固定容積的充放氣；活塞運動時，進氣腔和排氣腔的容積隨時間不斷發生變化，此時屬于變容積充放氣。充氣時，進氣腔氣體受到壓縮，溫度升高，進氣腔側元件包括氣缸壁、節流閥和氣管等和內部氣體進行熱交換而溫度升高；元件外部空氣溫度也由于元件溫度的升高而升高。放氣過程中，放氣腔氣體由于膨脹而溫度降低，放氣腔側元件和內部氣體進行熱交換而溫度降低；元件外部空氣溫度也由于元件溫度的降低而降低。

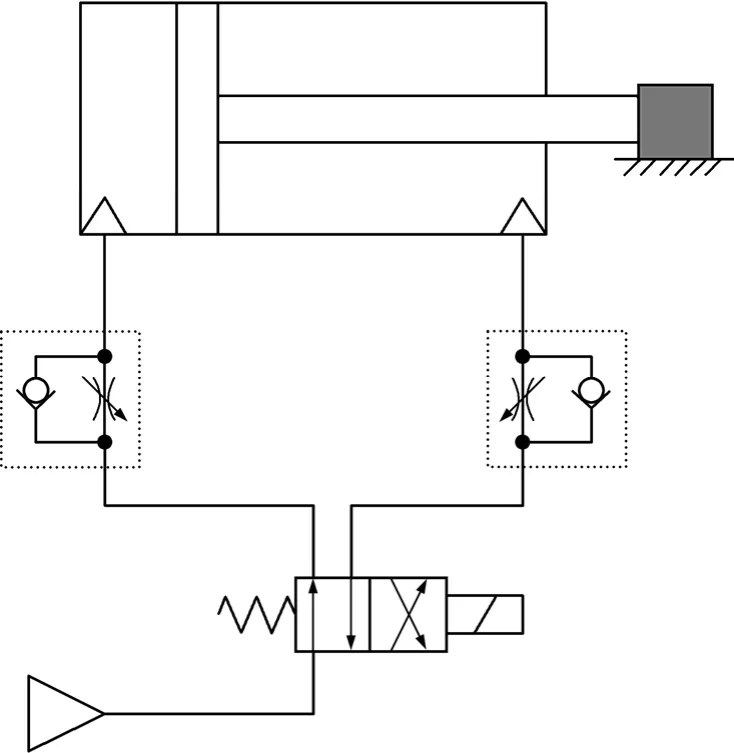
圖1 典型氣動回路Fig.1 Typical pneumatic circuit

1.1 數學模型的建立

氣體在充放氣系統中的流動屬于可壓縮湍流。二維控制方程如下。

(1) 連續性方程[12]：

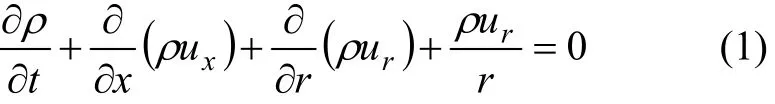
式中：ρ為空氣的密度；x為軸向坐標；r為徑向坐標；t為時間；ux為軸向速度；ur為徑向速度。

(2) 軸向和徑向的動量守恒方程：

(3) 能量方程：

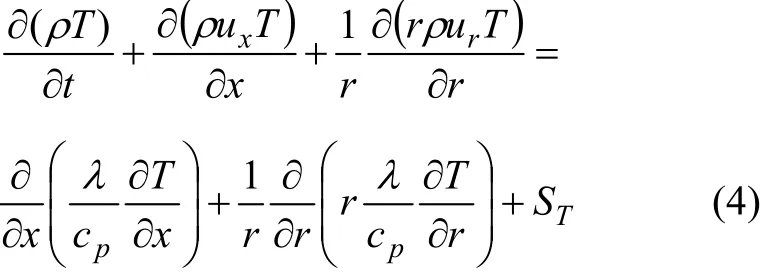
式中：T為氣體熱力學溫度；λ為導熱系數；cp為氣體的定壓比熱容；ST為廣義源項。

(4) 狀態方程：

式中：R為摩爾氣體常數。

(5) 活塞運動方程：

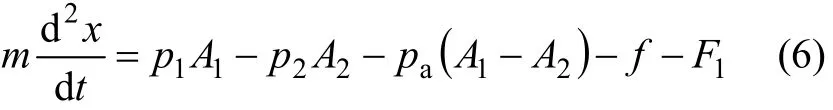
式中：m為活塞和負載質量；p1為氣缸無桿腔絕對壓力；p2為氣缸有桿腔絕對壓力；pa為大氣絕對壓力；A1為氣缸無桿腔側活塞面積；A2為氣缸有桿腔側活塞面積；f為摩擦力；F1為負載力。

(6) k-ε兩方程湍流模型[13]：

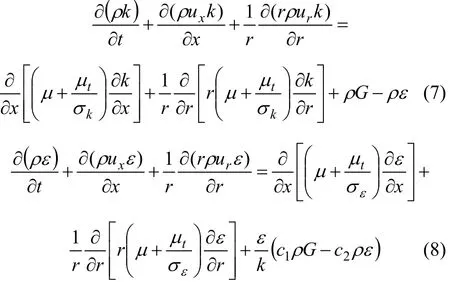
其中：

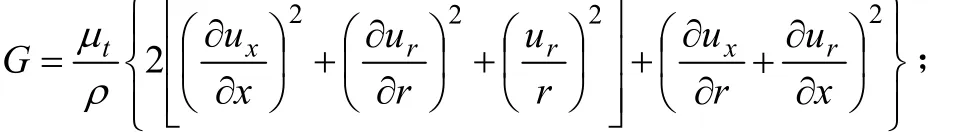
1.2 幾何模型及網格劃分

圖1所示的氣動系統具有復雜的三維結構。為了減少計算量，本文將氣缸簡化為圓柱體，將節流閥簡化為節流口，氣缸的進氣口和出氣口分別挪移到氣缸兩底面中心，如圖2所示。模型中的氣源區域與進氣管相連，為系統提供恒壓和恒溫的氣體。放氣管出口與大氣區域相連。

圖2 簡化的氣動回路模型Fig.2 Simple model of pneumatic circuit

簡化后的氣動回路進一步簡化為以水平中心線為對稱軸的二維模型。利用 Fluent軟件的前處理軟件Gambit建立二維模型，如圖2所示。

采用四邊形網格和三角形網格對模型進行分區域網格化。氣管和節流口等處采用較密的三角形網格，氣管壁等處采用四邊形網格。模型網格如圖3所示(由于尺寸限制只顯示進氣節流口處網格)。

圖3 模型網格Fig.3 Mesh of model

2 初始條件和邊界條件的設定

初始時模型中氣源區、氣缸放氣腔、放氣節流口與放氣管壓力均為供氣壓力，其他區域為大氣壓力。

邊界條件包括進氣口、放氣口和壁面等。進氣口為壓力入口邊界，壓力為供氣壓力，溫度為供氣溫度；放氣口為壓力出口邊界，壓力為大氣壓，溫度為大氣環境溫度。給定各壁面溫度，包括氣管壁面、節流閥壁面和氣缸壁面等。活塞的壁面設為對流傳熱。管壁、節流口壁和氣缸壁處為耦合壁面，計算內部氣體、壁面和外部氣體之間的熱傳遞。近壁面區采用標準壁面函數。

3 計算結果與分析

3.1 計算結果與試驗對比

為了驗證本方法的正確性，依照表1中參數建立模型，利用Fluent軟件進行計算。氣缸無桿腔為進氣腔，有桿腔為放氣腔。用 PISO法對壓力場和速度場進行求解。

運動方程通過自定義函數實現，實時讀取活塞兩側的壓力，根據式(6)計算得到活塞的速度并返回到模型中。活塞以相應速度運動使得進氣腔逐漸增大而排氣腔逐漸減小。

利用有限差分法建立相同參數的絕熱模型進行計算，同時，按照圖1和表1建立氣動回路進行充放氣試驗，測量氣缸兩腔壓力。進氣腔壓力如圖4所示，放氣腔壓力如圖5所示。

從圖4和5可以看出：與絕熱模型的計算結果相比，本方法的計算曲線與試驗曲線具有更好的一致性，表明了本方法的可行性和正確性。整個充放氣過程約為 0.55 s。初始時活塞靜止，充氣腔和放氣腔分別為定容充氣和定容放氣。在活塞伸出過程中，充氣腔壓力先升高后又降低，放氣腔壓力單調降低；充放氣0.33 s時，活塞桿完全伸出，活塞速度瞬時突變為零，充氣腔壓力逐漸增大為氣源壓力；放氣腔壓力迅速減小最終穩定為大氣壓。

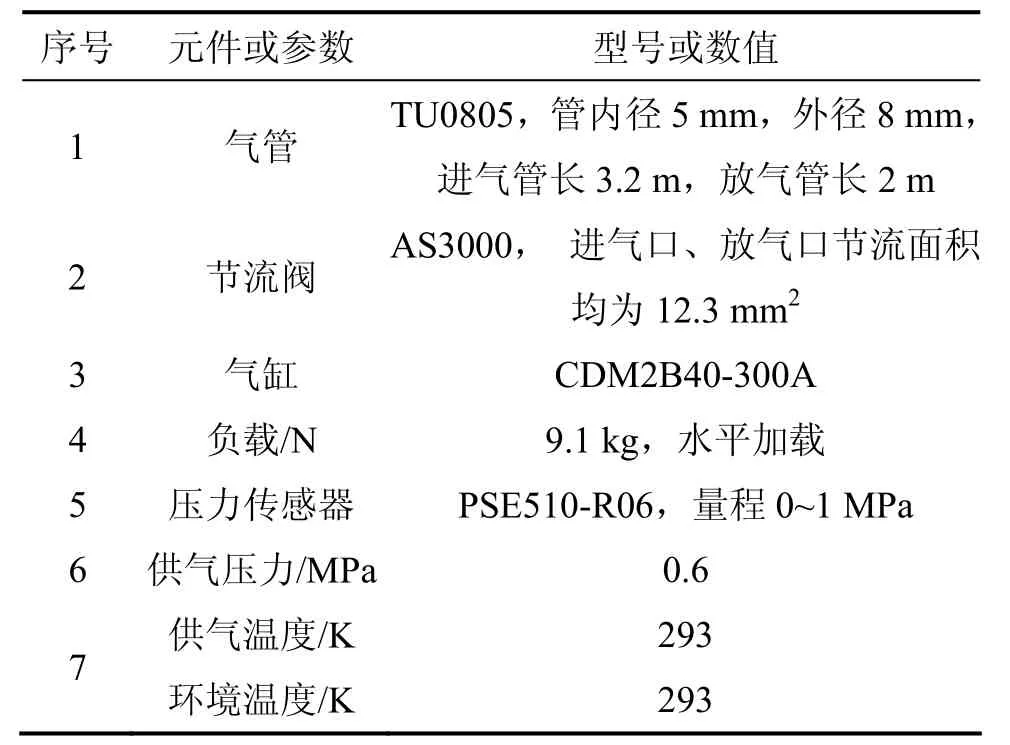
表1 元件參數Table 1 Parameters of components

圖4 氣缸進氣腔壓力曲線Fig.4 Pressure curves of charging chamber in cylinder

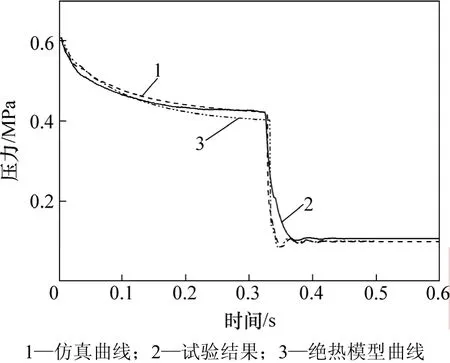
圖5 氣缸放氣腔壓力曲線Fig.5 Pressure curves of discharging chamber in cylinder

3.2 計算結果分析

圖 6所示為充放氣過程中放氣管軸線的壓力分布。放氣管長2 m，與放氣節流口連接處為起點，與大氣區域相連處即放氣管出口為末端。氣體經節流口進入放氣管，由于射流的作用壓力有明顯下降。在距管入口10～15倍管徑處回升到最大值，然后又逐漸降低，與文獻[14]中的結論一致。

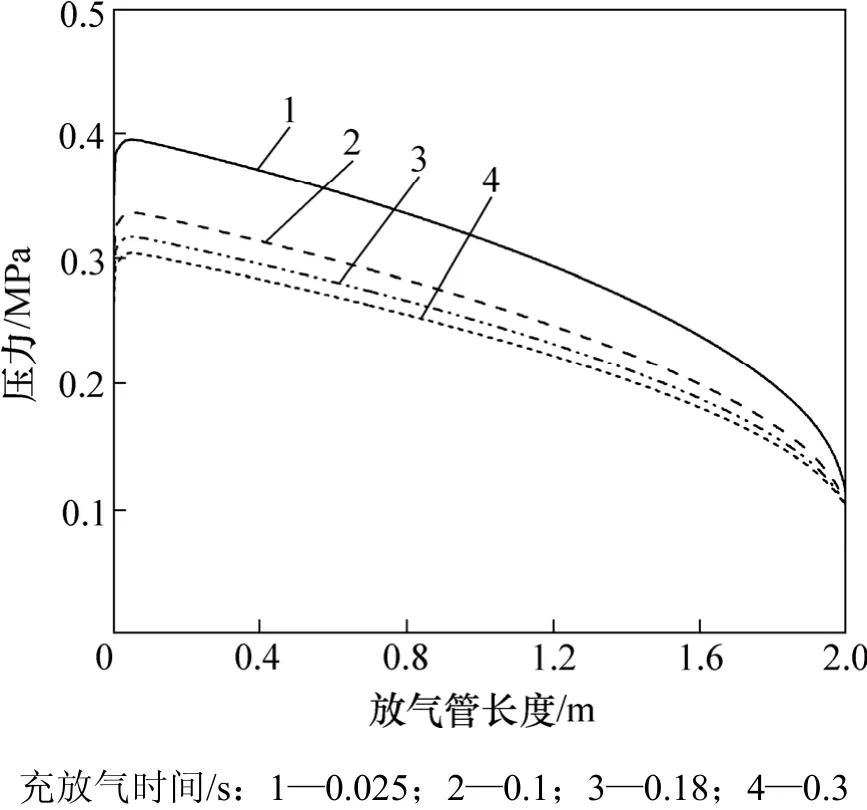
圖6 充放氣過程中放氣管內壓力分布Fig.6 Pressure distribution in discharging pipe during charging and discharging process

充放氣0.025 s和0.03 s時的馬赫數分布如圖7和8所示(由于尺寸限制只給出節流口處和放氣管出口處等值線)。

由圖7可見：充放氣0.025 s時在進氣節流口、放氣節流口和放氣管出口均有明顯速度梯度，馬赫數最大值為1.10，出現在放氣管出口處，處于超聲速范圍。在放氣管出口緊鄰的大氣區域中形成了明顯的射流區域，射流呈現向外發散的趨勢。由圖8可見：充放氣0.3 s進氣節流口、放氣節流口和放氣管出口的速度梯度較充放氣0.025 s時的速度梯度要小，馬赫數最大值為0.87，出現在放氣管出口處，處于亞聲速范圍，與充放氣0.025 s時的馬赫數分布有所不同。

充放氣0.1 s時氣缸內溫度等值線如圖9所示。由圖9可見：在節流口處較大的溫度梯度，在氣缸內壁附近的溫度梯度較為明顯，而氣缸內部的溫度較為均勻。氣體經過放氣節流口處時溫度迅速下降。

充放氣過程中元件不同部位的溫度曲線如圖 10所示。由圖10可見：在充放氣過程中，進氣管壁和進氣節流口壁面的溫度上升，溫度上升幅度與距進氣節流口的距離成反比，進氣節流口壁面溫度上升幅度最大。放氣管壁和放氣節流口壁面的溫度下降，放氣結束時，元件溫度由于熱交換而上升；溫度降幅最大的是放氣節流口壁面及與節流口緊鄰的氣管壁面，這與文獻[15]中的結論一致。

圖7 充放氣0.025 s時馬赫數分布Fig.7 Mach number after charging and discharging for 0.025 s

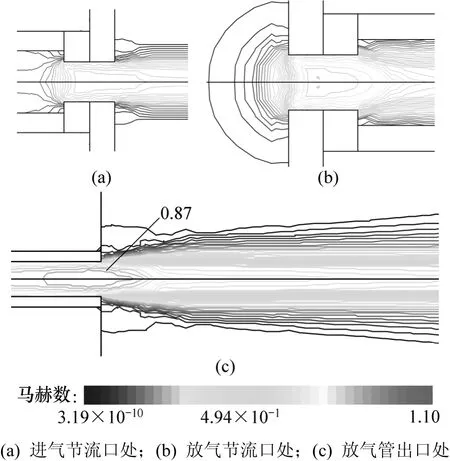
圖8 充放氣0.3 s時馬赫數分布Fig.8 Mach number after charging and discharging for 0.3 s

圖9 充放氣0.1 s時溫度等值線Fig.9 Temperature isolines after charging and discharging for 0.1 s

圖10 元件壁面溫度Fig.10 Temperature of components

4 結論

(1) 以典型氣動充放氣系統為研究對象，根據實際條件適當簡化，將實際氣動回路簡化為二維軸對稱模型，采用動網格技術實現了對氣動充放氣系統內部流場的詳細計算。

(2) 在充放氣過程中，氣體經放氣節流口進入放氣管后壓力下降，在距入口10～15倍管徑處達到最大值，符合實際。放氣時，速度最大值可達到超聲速范圍，出現在放氣管出口處。放氣管出口處存在著明顯的射流區域。流場計算時在管路出口設置大氣區域更符合實際。

(3) 充放氣過程中氣缸內溫度梯度主要存在于內壁處。進氣節流口壁面的溫度上升幅度最大，放氣節流口及緊鄰的氣管壁面溫度降幅最大。

(4) 通過計算可以得到氣動系統內部流場不同時刻的狀態參數，為研究內部流場提供了參考，其與試驗結果的對比結果證明了該方法具有較高的準確性。

[1] H?ier C K, Sonnenborg T O, Jensen K H, et al. Experimental investigation of pneumatic soil vapor extraction[J]. Journal of Contaminant Hydrology, 2007, 89(1): 29-47.

[2] Yamada T, Watanabe T. Development of a pneumatic cylinder-driven arm wrestling robot system[C]//Proceedings of the 17th IEEE International Symposium on Robot and Human Interactive Communication. Munich, Germany, 2008: 665-670.

[3] 金英子, 朱祖超, 楊慶俊, 等. 氣動系統充放氣過程中氣體狀態多變指數的簡化與確定[J]. 機械工程學報, 2005, 41(6):76-80.JIN Ying-zi, ZHU Zu-chao, YANG Qing-jun, et al.Simplification and determination of polytropic exponent of thermodynamic process in the filling and exhausting process in a pneumatic system[J]. Chinese Journal of Mechanical Engineering, 2005, 41(6): 76-80.

[4] Carneiro J F, Almeida F. Heat transfer evaluation of industrial pneumatic cylinders[J]. Journal of Systems and Control Engineering, 2007, 221(1): 119-128.

[5] Berger H. Numerical simulation of gas flow in pneumatic components[J]. Journal of Forschung im Ingenieurwesen:Engineering Research, 1992, 58(3): 67-74.

[6] 李軍, 楊慶俊, 王祖溫. 氣動系統內部結露機理及實驗[J]. 機械工程學, 2007, 43(9) : 7-11.LI Jun, YANG Qing-jun, WANG Zu-wen. Mechanism and experiment of the internal condensation of water vapor in pneumatic system[J]. Chinese Journal of Mechanical Engineering, 2007, 43(9): 7-11.

[7] 李玉軍, 王祖溫, 包鋼. 考慮管路特性的氣動系統的流場計算[J]. 熱能動力工程, 2000, 15(5): 506-509.LI Yu-jun, WANG Zu-wen, BAO Gang. The calculation of a pneumatic system flow field with the pipe channel characteristic being taken into account[J]. Journal of Engineering for Thermal Energy & Power, 2000, 15(5): 506-509.

[8] 楊麗紅. 容器放氣過程的數值模擬及熱力學模型研究[D]. 上海: 上海交通大學機械與動力工程學院, 2007: 29-44.YANG Li-hong. Study on the numerical simulation and the thermodynamic model of the tank discharge process[D].Shanghai: Shanghai Jiao Tong University. School of Mechanical and Power Engineering, 2007: 29-44.

[9] 王瑞金, 張凱, 王剛. Fluent技術基礎與應用實例[M]. 北京:清華大學出版社, 2007: 175-204.WANG Rui-jin, ZHANG Kai, WANG Gang. Fluent technology foundation and examples of application[M]. Beijing: Tsinghua University Press, 2007: 175-204.

[10] 王福軍.計算流體動力學分析-CFD 軟件原理與應用[M].北京:清華大學出版社, 2004: 248-252.WANG Fu-jun. Analysis of computational fluid dynamicsprinciple and application of CFD software[M]. Beijing: Tsinghua University Press, 2004: 248-252.

[11] 胡軍強, 俞小莉, 劉林, 等. 氣動發動機缸內流場的動態特征[J]. 浙江大學學報: 工學版, 2007, 41(11): 1912-1915.HU Jun-qiang, YU Xiao-li, LIU Lin, et al. Dynamic characteristics of in-cylinder flow field in air-powered engine[J].Journal of Zhejiang University: Engineering Science, 2007,41(11): 1912-1915.

[12] Reynier P, Minh H H. Numerical prediction of unsteady compressible turbulent coaxial jets[J]. Journal of Computers &Fluids, 1998, 27(2): 239-254.

[13] 陶文銓. 數值傳熱學[M]. 2版. 西安:西安交通大學出版社,2001: 332-351.TAO Wen-quan. Numerical heat transfer[M]. 2nd ed. Xi’an:Xi’an Jiaotong University Press, 2001: 332-351.

[14] 包鋼, 李玉軍, 李軍, 等. 氣動系統中管路的二維粘性流場計算[J].熱能動力工程, 2001, 16(5): 499-502.BAO Gang, LI Yu-jun, LI Jun, et al. Calculation of a two-dimensional viscous flow field in the pipe of a pneumatic system[J]. Journal of Engineering for Thermal Energy & Power,2001, 16(5): 499-502.

[15] ZHU Dong, YANG Qing-jun, BAO Gang. Study on principles of external condensation of water vapor in pneumatic system[C]//Proceedings of the 7th International Conference on Fluid Power Transmission and Control. Hangzhou, 2009:604-607.