磁異常共軛元反演解釋法研究

晏月平 ，戴前偉，蔡家雄 ，魯光銀

(1. 中南大學 地球科學與信息物理學院，湖南 長沙，410083；2. 湖南省有色地質勘查局，湖南 長沙，410000；3. 湖南省國土資源廳，湖南 長沙，410004)

以復變函數[1]為基礎、建立于經典靜位場理論基礎之上的磁法勘探方法[2-3]，由于正演理論較其他地球物理勘探方法成熟，所以，率先在計算機上實現了一系列的反演方法和技術，尤其是近30年來，隨著電子計算機的廣泛應用，地球物理反演的理論和方法得到了極大的發展[4-5]。Backus-Gilbert反演理論[6]、廣義逆矩陣理論、統計參數估計、最小二乘參數估計、最大似然法參數估計、正則化理論、約束最優化、動態規劃、遺傳算法[7]、神經網絡法[8]等得到應用。這些方法在磁法反演上的共同特點是，在觀測數據與模型之間建立一種函數關系，在解釋過程中不斷修改模型參數[9-10]，不斷評價觀測值與理論模型計算值的擬合程度，最后通過某種評判標準中斷反演進程求得最終模型。它們的實質都是完全以位場理論為基礎尋求獲得穩定解和收斂速度的計算方法，由于過多依賴于計算技巧的運用，在理論上難以有實質性的突破，同時，這些方法在解釋過程中有一系列近似條件的設定和線性方程組[11]的求解，這些過程勢必導致誤差累加，影響反演結果的真實性。特征點法[12]是一種簡便而快速的定量解釋方法，解釋是以剖面磁異常特征為基礎，但由于缺少完整的數學模型，依賴于經驗積累和簡單的幾何運算，其定量計算結果難以取得好的效果，尤其對復雜異常或迭加異常，特征點解釋法更是難以進行。本文作者提出的方法其理論原形可以追溯到特征點法，但方法的實質和求解過程遠遠超出了特征點法的概念范疇。它試圖擺脫現有各類反演方法，以板狀體磁異常為切入點，以磁異常平面和剖面特征為突破對象，通過提取異常共軛元等特征參數，建立磁異常圖形變換的數理模型，并以變換圖形的手段實現磁異常的反演解釋，期望為磁法勘探的正反演計算提供新的途徑。

1 板體磁場計算公式

對特定地理環境下的板狀體，已知板體寬度2b，板體走向長度為2L，板體下延長度為l，上項埋深為h，板傾角為β，中心點坐標為x0等，如圖1所示。若知道地磁場傾角I0、板體走向與磁北的夾角A和剖面內有效磁化傾角is，則剖面任意點處總強度磁異常ΔT計算公式[13]為：

圖1 薄板體幾何及磁場要素圖Fig.1 Thin body geometry and magnetic field elements

式(1)最初由Grant提出[13]，該公式對三度、似二度、二度異常均較適用，但由于在角度處理上存在問題，因而，一直未能得到推廣使用。本文在利用此式前對相關錯誤進行糾正，并通過理論模型驗算。本文提出的公式是修正后的公式。

2 共軛三角形建立及圖形轉換

磁異常共軛三角形及共軛元如圖2所示。圖2中曲線為單一板體磁異常曲線，異常包含了峰值區和谷值區2個主要部分。在圖2中，線段AB和AV所在直線分別是通過峰值左翼拐點P1和右翼拐點P2的切線，線段VC所在直線是通過谷值區右翼拐點P3的切線，3條線段交匯構成一對底邊平行，并以AV為公共邊的三角形，這里稱之為共軛三角形，其中三角形BAV與板體磁場峰值區對應，形象地稱為“A型”三角形；三角形AVC與谷值區對應，形象地稱為“V”型三角形，線段AV稱為共軛邊。三角形的高AU及VW將底邊分成 BU，UV，AW 和 WC，顯然，a，c，d和e這4個線段反映了共軛三角形的固有屬性，也包含了豐富的磁異常信息，它們定義了一個完整的共軛三角形，這里稱為共軛元。

根據式(1)一階導數、二階導數的數學意義[1]，可以計算出通過拐點P1，P2和P3的斜率k1，k2和k3及4個共軛元a，c，d和e。顯然，共軛元是與板狀體幾何參數及磁場參數相關的初等函數，考慮到磁矩 Ms與磁化強度J及板體寬度b具有正比關系，共軛元的計算可以用通式表示為：

其中：g ∈(a,c,d,e)。

將G函數定義為共軛元函數，并把根據磁異常曲線求取共軛元函數的過程稱為磁異常的圖形轉換。圖形轉換建立了共軛元與板體各要素 ),,,,(sLlhMξ 的函數關系，為異常特征信息直接進入反演過程奠定了理論基礎。

通過式(1)求取一階、二階導數的過程是非常繁瑣的過程，求解結果是一個相當復雜且包含板狀體全部要素的五次方程，因而共軛元的精確解析非常復雜，必要時需借助數學工具，通過限定精度采取迭代法求解。

圖2 磁異常共軛三角形及共軛元Fig.2 Magnetic anomaly conjugate triangle and conjugate element

3 共軛比值定義

下面定義2個比值：

BA′和Bv反映了共軛三角形的畸異特性，包含了磁異常曲線的許多異常特征，定義為共軛比值。由于其計算過程實際上是共軛元函數的四則運算過程，因而，其計算通式可以表示為：

其中： B ∈ ( BA′,Bv)。

為了討論問題方便，以BA′為縱軸，Bv為橫軸定義一個共軛坐標系，數據對(BA′, Bv)稱為共軛坐標。

在式(5)中，與板狀體幾何形態相關的參數為ξ，L和l，這3個參量也是影響磁場分布特征的關鍵因素，也往往是異常反演解釋時的重要目標參量[14]。為了簡化求解過程，需要設定初始條件，暫時將Ms和h看成常量，令其等于1個單位，而走向長度L也可以近似于異常走向長度 Cd，即令 L/h=Cd。簡化后式(5)可以寫成：

式(6)表明：在初始條件下，決定共軛坐標形態的參量只有2個。

設定邊界條件如下：有效磁化傾角is=60°，L/h=3，討論ξ和l/h變化時共軛坐標軌跡的一些特征。

首先分別令 l/h為 0.5，1.0，1.5，2.0，2.5，3.0和3.5，連續變化ξ，通過搜索得到的共軛坐標軌跡是一系列封閉或近似封閉的曲線，即圖3中虛線，形象地稱為共軛緯線。

同理，分別令ξ等于某一固定值，連續變化l/h，則搜索得到的共軛坐標軌跡是一系列向外發散的放射狀曲線，即圖3中實線，形象地稱為共軛經線。

圖3 ΔT磁異常共軛網絡Fig.3 Magnetic anomaly conjugate network diagram

圖3 中經線與緯線組成了一個網狀圖形，稱為共軛網絡圖。搜索網絡中的點(例如點P)或某個網格塊可以初步確定板狀體傾角、下延長度等參數值或其變化范圍。

因而，一個異常的2個共軛比值A′B和Bv，在分別以A′B和Bv為縱、橫坐標的共軛坐標系中形成一個共軛點。無數邊界條件相同的共軛點以變化磁性體傾角的共軛點軌跡形成共軛緯線；變化磁性體下延長度的共軛點軌跡形成共軛經線；并以傾角為0°、下延長度近似為0的共軛點為共軛“芯點”。一定邊界條件的共軛坐標、經緯線、芯點組成一幅形似蓓蕾的“共軛網絡圖”。

邊界條件確定的共軛點在共軛網絡中具有唯一性。這是最重要的性質。利用這一性質，通過坐標逐步搜索，即可優先精確地解出ξ與l/h這2個參數，其中ξ是最重要的關鍵參數。ξ被優先得出，是采用共軛元突破磁異常全參量解釋的重要貢獻。

4 磁異常共軛元反演解釋

基于共軛元求取磁異常磁源體幾何、磁性參數的過程簡稱為磁異常的共軛元反演解釋。一個完整異常的共軛元反演解釋由共軛解釋與校正解釋 2部分組成，解釋過程可由程序根據異常的特征參數自動完成。

4.1 共軛解釋

在實際應用中，通過幾何作圖法或曲線拐點追蹤算法[14]求出實測磁異常的共軛元，利用式(3)和(4)計算共軛坐標點(A′B, Bv)。然后利用式(6)，不斷變化板狀體要素ξ和l/h求取共軛點，通過多次迭代，可以使求取的共軛點逼近實測的共軛點(A′B, Bv)。當滿足設定條件時，可以將ξ和l/h作為最終結果。因此，共軛元反演解釋過程實際上包括2個主要環節，即圖形變換與變換圖形。變換圖形是指逐步變換共軛三角形的圖形，在相同邊界條件的共軛網絡圖中，搜索到由實測異常確定的共軛點的位置。在解釋過程中，每一個共軛點都是通過設定參數去計算異常，并經圖形變換為共軛三角形后計算獲得。因此，實測異常確定的共軛點與解釋過程中的共軛點之間的本質差異是：前者雖包容了實測異常中的重要信息，但全部是未知的；后者在解釋過程中雖與實測異常暫無關系，但其異常中的所有參數均是具體的。在幾何上可以證明：當2點重合后，實測異常的共軛三角形與解釋異常的共軛三角形為相似三角形。在實測異常與解釋異常共軛點重合時，根據相似原理變未知為已知，則可解出異常體的全部未知參數。下面對這一過程進一步說明。

當共軛點確定后，據共軛經線坐標得出ξ，據共軛緯線坐標得出l/h。該過程完成時，相當于在共軛解釋子程序中，建立了一個以磁體上頂埋深、磁矩為單位(都等于1)的“相似共軛三角形”。

由圖形變換得到的共軛三角形，其中有關磁性體的參數是完全未知的。而相似共軛三角形中除優先解出ξ和lt/h外(由于前述l非最終值，暫令lt=l)，還可以給出：

因此，利用共軛三角形與相似共軛三角形中對應參數的等比性質，并令M (ξ)=，則有：

式(9)～(12)分別是共軛法求解磁矩、磁性體上頂埋深、下延長度、傾角的定量解釋公式；式(13)是磁性體半長度的半定量解釋公式，其中，Cd為異常走向長度，是L/h的近似數。

定量解釋實測異常時，還有2個公式也相當重要：

式(14)和(15)分別是異常的原點、正常場定量解釋公式。其中：Ax是共軛三角形頂點與磁性體上頂中心在地表投影點間的橫坐標；To是共軛三角形頂點至正常場間的縱坐標。同樣，A(ξ)和T ( ξ)是以ξ為變量的函系數。T(ξ)等所有函系數均是某一常量的倒數，因此，磁性體有關參數的求解均十分簡便。

4.2 校正解釋

校正解釋是指異常經剖面解釋后，為校除因“近似數Cd”給解釋結果帶來的誤差，根據磁異常平面特征參數，校正用于剖面解釋中的L/h代數值，進而完善解釋結果的過程。

地磁傾角以及異常體走向半長度與埋深之比(L/h)是共軛解釋的2個不可或缺的邊界條件。但在共軛元解釋過程中，L/h選用數值十分相近Cd參數代替。因此，解釋結果存在誤差。

校正解釋中涉及的參數都是與異常平面特征有關的特征參數見圖4。

圖4 異常平面特征點及要素Fig.4 Abnormal plane feature point and factor

圖4 中：GMN為極值距，指異常平面圖中的極值間距；R為極線角，是極值連線與磁北之間的夾角；G23為長軸拐點距，為異常平面圖中異常長軸上拐點之間的坐標量；為正負異常極值點距離。

圖4中：GMN=；R=∠OMN； G23= G2-G3。

當異常長軸方位角A＜45°時，GMN與2L之間在量值上有近似相等的關系；當異常長軸方位角A＞45°時，G23與2L之間，在量值上有近似相等的關系。因此，選擇了GMN與LG作為長深比Cd的代數。

當-45°＜A＜45°時，

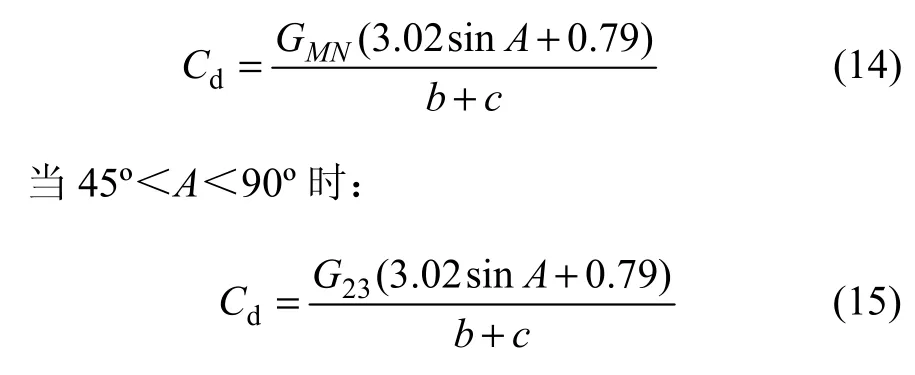
在一般情況下，Cd與L/h具有較高的近似程度。倘若長深比Cd等于L/h，則剖面解釋階段即會得到精確的解釋結果，繪制的解釋結果平面等值線圖必定與給定異常平面等值線圖完全一致。同時，解釋結果的剖面曲線與給定異常剖面曲線之間也會高度擬合；假若Cd小于或大于L/h，則解釋結果平面等值線圖的長軸會明顯減短或加長，同時解釋結果剖面曲線與給定異常剖面曲線之間擬合后會出現明顯的剩余異常。可見，解釋結果的誤差主要來源于Cd。因此，校正解釋過程是校正Cd的過程。

校正解釋是在完成共軛解釋基礎上進行的。校正有2種途徑：

(1) 利用共軛解釋前、后異常平面圖中的“極間距”與“極線角”差異完成校正。

(2) 利用共軛解釋前、后異常平面圖中的“極間距”與“長軸拐點距”比值完成校正。

當-45°＜A＜45°時：

式中：Cxz，CJS和LJS分別為長深比代數校正值、解釋結果平面異常的極間距、解釋結果平面異常的長軸拐點間距。

采用式(16)對一模型異常進行反演計算，其模型參數、共軛解釋結果、校正結果及校正誤差見表 1，可見：通過校正解釋后，解釋結果相對誤差不大于1%，6個模型參數均得到了精確解釋結果。

表1 理論模型磁異常共軛元反演解釋過程參數表Table1 Theoretical model of magnetic anomaly conjugate element inverse interpretation process parameter

實踐中，給定異常的參數都是未知的，解釋結果中不可能給出模型參數誤差水平；因此，可靠性的鑒別要靠異常剖面的擬合與平面圖的比照完成。

當異常剖面擬合后出現明顯剩余異常時，表明尚未得到最佳解釋結果，這是ΔT磁異常共軛解釋法的剖面判別；當進行平面圖異常比照后，如果異常形態基本一致，但展布面積與異常極值有明顯差異，亦表明尚未得到最佳解釋結果，這是ΔT磁異常共軛元解釋法的平面鑒別。通過剖面判別與平面鑒別，采用ΔT磁異常共軛解釋法均可得到相對精確而可信的解釋結果。

5 實例

共軛元反演在廣東省、湖南省、青海省得到多次應用，均取得了較好的應用效果。現以廣東某鐵礦[15]為例，闡明其應用過程與效果。

區內地磁傾角為34.4°，異常圈定基本完整(圖5)。異常的長短軸比值約為3.5。利用N44線磁異常進行共軛元反演解釋。異常曲線總體具有單體異常的曲線特征，但經過逐步解釋后發現，異常由3個磁性體疊加引起。其解釋結果如表2及圖5所示。

表2 廣東某磁鐵礦N44線磁異常共軛元反演解釋結果Table2 A magnetite magnetic anomaly conjugate element inverse interpretation results for Line44

表2中，接觸帶指灰巖與花崗巖接觸部位。剖面解釋結果表明：實測磁異常與反演結果模型磁異常的平面圖及剖面圖展示的異常形態、展布范圍、幅值特征基本吻合；鉆孔見礦深度與反演模型通過部位基本吻合，解釋結果得到的外接觸帶磁性體磁性強度更高且無鉆孔控制，為盲礦體的可能性大。實例反演結果較充分地體現了共軛元反演解釋方法的實用性、可靠性及在異常識別、異常分解等方面的優越性。

圖5 廣東某磁鐵礦磁異常共軛元反演解釋結果Fig.5 Magnetite magnetic anomaly conjugate element inverse interpretation results

6 結論

(1) 共軛元反演解釋是通過提取磁異常剖面特征和平面特征實現磁異常的圖形轉換，在解釋過程中不斷細化對異常特征的認識，最后得出磁性體幾何參數和磁場參數的反演方法。

(2) 在解釋過程中考慮了磁異常平面信息，但又不完全依賴于平面信息的完整程度，該方法在提高解釋結果可靠性的同時，較大限度地放寬了方法的應用條件。在反演過程中沒有復雜的數學運算和大型方程的求解，可以大大提高反演效率，減少反演期間的累加誤差。

(3) 雖然該方法是建立在薄板體磁異常的基礎之上，但由于該方法同樣滿足迭加原理，因而可以通過不同特征薄板體的迭加實現諸如二度體、三度體等模型體的反演。該方法具有較大的研究空間和廣闊的應用前景。模型試算和實例結果表明：其解釋結果具有較高的精度和可靠性。

[1] 安玉林, 譚保華. 局部重磁場源全方位成像[M]. 北京: 地質出版社, 1997: 3-16.

AN Yu-lin, TAN Bao-hua. Omnidirectional imagery of local gravity and magnetic anomaly sources[M]. Beijing: Geological Press, 1997: 3-16.

[2] 管志寧. 地磁場與磁法勘探[M]. 北京: 地質出版社, 2005:85-160.

GUAN Zhi-ning. Geomagnetic field and magnetic exploration[M]. Beijing: Geological Press, 2005: 85-160.

[3] 劉天佑. 位場勘探數據處理新方法[M]. 北京: 科學出版社,2007: 1-85.

LIU Tian-you. New data processing methods for potential field exploration[M]. Beijing: Science Press, 2007: 1-85.

[4] 劉天佑. 重磁異常反演理論與方法[M]. 北京: 中國地質大學出版社, 1992: 19-88.

LIU Tian-you. The theory and method on inversion of gravity and magnetic anomalies[M]. Beijing: The Press of China University of Geosciences, 1992: 19-88.

[5] John A. Introductory geophysical inverse theory[M]. Colorado:Samizdat Press, 2001: 183-185.

[6] Snieder R. An extension of Backus-Gilbert theory to nonlinear inverse problems[J]. Inverse Problems, 1991(7): 409-433.

[7] 趙改善. 求解非線性最優化問題的遺傳算法[J]. 地球物理學進展, 1992, 7(1): 90-97.

ZHAO Gai-shan. Nonlinear optimization using genetic algorithms[J]. Progress in Geophysics, 1992, 7(1): 90-97.

[8] Raiche A. A pattern recognitionapproach to geophysical inversion using neural nets[J]. Geophysics J Int, 1991, 105(3):629-648.

[9] Tarantola A. Inverse problem theory and methods for model parameter estimation[M]. The Society for Industrial and Applied Mathematics, 2005: 1-40.

[10] Anderssen R S, Seneta E. Asimple statistical estimation procedure for Monte-Carlo inversion in geophysics[J]. Pure Appl Geophys, 1971, 96(1): 5-14.

[11] Nabighian M N. Toward a tree-dimensional automatic interpretation of potential field data via generalized Hilbert transforms: Fundamental relations[J]. Geophysics, 1984, 49(6):780-786.

[12] 劉天佑. 地球物理勘探概論[M]. 北京: 地質出版社, 2007:122-124.

LIU Tian-you. Conspectuss of geophysical exploration[M].Beijing: Geological Press, 2007: 122-124.

[13] Grant F S. Interpretation theory applied geoghysics[M]. US: Mc Graw-Hill Book Company, 1965: 307-354.

[14] Nabighian N N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section[J]. Geophysics,1972, 37(3): 507-517.

[15] 伍卓鶴, 何俊美. 粵中-粵東地區區域重力成果[J]. 物探與化探, 2007, 31(5): 435-439.

WU Zhuo-he, HE Jun-mei. Achievements of regional gravity survey in central and eastern Guangdong Province[J].Geophysical and Geochemical Exploration, 2007, 31(5):435-439.