顧及未知系統誤差的變形監測濾波算法

左廷英，曾 磊

(中南大學 地球科學與信息物理學院，湖南 長沙，410083)

滑坡的變形過程受多方面因素的影響[1-2]。人們對邊坡的物理狀態信息的認識和假設等，都會影響各測點的位移速率，使滑坡的位移時序曲線表現出波動性，從而使滑坡動態分析的難度增加，建立的模型無疑會包含一定程度的誤差[3-8]，進而導致形變分析結果不精確。計算邊坡形變的一種合理的方法是：將邊坡物理模型估計的形變量與幾何觀測量相結合建立混合模型。這種混合模型最早由 Schwintzer[9]提出；Bock等[10-11]對此進行了進一步的研究，他們根據地球物理模型和實測擬合模型之間的差異, 應用抗差估計來調整先驗參數對計算結果的影響。Segall等[12]提出“模型調整”法，即通過幾何模型計算的位移和物理模型預測位移之間的差異達到最小的原則來求解形變量。在實際跟蹤滑坡的動態變化過程中，總是存在一些未知邊坡物理信息，它們通常只有微小的變化，在固定的觀測歷元間可以看成是常量，或圍繞某常量隨機變化，因此，可以采用固定窗口內的觀測殘差和狀態預測殘差對它們進行擬合[13]，并給出相應協方差矩陣的近似估計。這種估計方法的優點是：在 Kalman濾波過程中，不僅能夠減小因物理信息不充分而導致的系統偏差的影響，而且可以求出這些系統偏差，即從函數模型和隨機模型2方面同時提高濾波結果的可靠性。

1 帶有模型誤差的濾波算法

在動態方程中，帶有未知模型誤差的濾波模型為：

其中：Xk為 tk時刻的狀態向量；Фk,k-1為狀態轉移矩陣；sk為未知的模型誤差；Wk為動力模型噪聲向量；Lk為觀測向量；Hk為設計矩陣；ek為觀測誤差向量。

sk=0時的濾波模型為：

它的預測向量為：

實踐中，如何求解sk的估計值仍需進一步研究。在固定的觀測歷元間視模型系統誤差為常量，或圍繞某常量隨機變化，則可以采用固定窗口內的觀測殘差和狀態預測殘差進行擬合，最簡單的方法是取平均值。根據前面的定義，sk為動力模型的系統誤差，而動力模型系統誤差應主要反映狀態預報值的偏差。根據式(5)，在tk-i，應有：

若假設動力學模型系統偏差在短時間(tk-N～tk)內維持微小變化，即滿足 E ( Wk-i) =sk，則預測狀態向量殘差的期望應該為0，即) = 0。顯然，將(6)式兩端取和，再除以N，并考慮，有：

可以證明：由式(7)求得的s?k為sk的無偏估計。因為已經假定由表示的含有系統誤差，故理論上應有，式(7)可改寫為

式(9)表明：由式(7)求得的動力模型系統誤差s?k是sk的無偏估計。

2 邊坡滑坡的濾波模型

根據滑動面的類型，邊坡滑坡可分為平面型、契型、曲面型和傾倒型等多種形式[14]。若把邊坡滑坡視為平面問題，則它們都可用一個塊體系統來描述(見圖1), 即滑體可以視為由許多小的塊體組成。本文中只考慮圖1所示的塊體系統。為了使問題簡化，假設塊體都是剛體。若塊體的幾何形狀和力學性質都是已知的，則可以導出塊體系統的運動方程。由牛頓第二定律可知，塊體系統中的任何一塊剛體的受力狀態見圖2，其運動可表示為：

其中：aix和aiz分別為第i塊剛體在x方向和z方向的加速度；N為正壓力；R為摩擦阻力；Nx和Nz分別為N在x和z方向的分量；Rx和Rz分別為R在x和z方向的分量；m為塊體的質量；g為重力加速度；xi和zi為塊體在x和z方向的位移；P和T為相鄰塊對它的作用力；t為時間。

方程 (14) 也可表示為：

圖1 塊體系統Fig.1 Block system

圖2 某一剛體的受力狀態Fig.2 Geometry and forces associated with a rigid block

對于整個塊體系統，由式(15)可構成如下方程組：

M 和A1由Mi和A1i組成。

方程(16)表示的是 1個剛體系統的運動方程，若系統中只有1個塊體，則必有：

為了提高計算精度，對參數 Y進行如下變換：Y=Y0+ΔY(其中，Y0是 Y在邊坡滑體處于極限平衡狀態下的取值)。由于在極限平衡狀態下，任意塊體的加速度都為0，即axi=azi=0，故由式(16)可得：

G0和C0是G在極限平衡狀態下的取值。由式(16)和(18)可得：

其中：Δ Y = Y -Y0; X1=(x1, z1, … ,xi, zi…)T，為位移向量； Δ G = G - G0= ( 0, Δ m1g , … , 0, Δ mig ,…)；V = X˙1=… ,vxi, vzi,…)T，為速度向量；a=V˙= ( ax1, az1,… ,axi, azi,…)T。顯然，ΔY 表示邊坡滑體的當前狀態與穩定狀態之間的差別。邊坡滑體的狀態可用下列狀態向量來描述：

按照剛體的運動方程，當剛體的運動從狀態k 轉移到k+1時，其位移和速度按下式變化：

除了雨后引起的地下水位變化和地震引起的震動外，在實際工作中，作用在邊坡滑體上的外力一般是保持不變的；因此，可以假定ΔG=0及ΔYk+1=ΔYk。若外力產生變化，則只要這種變化很小，可以視為狀態轉移誤差(系統噪聲)，根據這一假設和方程(19)可得：

由式(20)和(21)可得狀態轉移方程：

模型(12)考慮了邊坡運動的加速度，但在一般情況下，邊坡在發生滑坡突變之前的滑移過程中，移動的加速度非常小，在絕大多數情況下，加速度如果能達1 cm/d2將預示滑坡將發生，而加速度1 cm/d2在運動學上則非常小，因此，可在模型(22)中刪除加速度項，得到下列模型：

由于邊塊的物理信息并不充分，不能得到sk的具體值，因此，在濾波過程中，把它看作未知輸入信息。用Xk表示狀態變量代替式(23)中的Xk′，由式(23)可以得到帶有未知輸入的變形監測濾波模型(見式(1))。

3 實例解算與分析

以湖南某高速公路邊坡監測為例。該邊坡已采用抗滑樁進行處治，邊坡質量未知，在抗滑樁上布設觀測點，觀測其三維位移。采用GPS連續靜態模式觀測，采樣時間為15 s，基線每3 h計算1次結果，共觀測6月，約1 500個結果。 X1,k+1=(Xk, Yk, Zk)T；V1,k+1=(其中：X和Y分別為x和y水平方向位移，Z為沉降)。由于監測點布置在抗滑樁上，抗滑樁主要向公路傾斜(即水平位移)，沉降較小。為了說明所提出的該方法的優越性，本文按照剛體的運動方程，當剛體的運動從狀態k 轉移到k+1時，其位移和速度按式(20)變化，設計了以下2種計算方案。

方案 1 采用常見的卡爾曼濾波中最常見的動態方程，在這個動態方程里只考慮了剛體的運動，不考慮邊坡的物理信息。

方案 2 除了雨后引起的地下水位變化和地震引起的震動外，在實際工作中，認為作用在邊坡滑體上的外力一般是保持不變的。因此，可以假定ΔG=0及ΔYk+1=ΔYk。若外力產生變化，則只要這種變化很小，可以視為狀態轉移誤差(系統噪聲)。

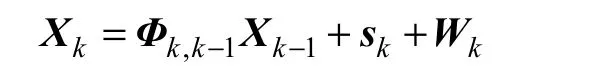
由于邊塊的物理信息并不充分，不能得到sk的具體值，因此，在濾波過程中，把它看作未知輸入信息，采用本文給出的算法進行濾波解算。

圖3和圖4分別給出了方案1和方案2的計算結果。對比圖3和圖4可以看出：

(1) 受觀測誤差和基準點系統誤差的雙重影響，采用方案1求得的點位形變不僅不光滑, 精度也較低(見圖3)。由于物理模型的誤差具有系統性質, 由此求得的形變位移仍然存在較明顯的系統誤差。

(2) 在方案 2中，因為增加了點位的物理信息，采用未知的物理信息進行擬合，部分地平衡了地球物理模型信息和觀測信息對滑坡預測的貢獻，精度明顯提高(見圖4)。

(3) 在邊坡監測實踐中，人們往往不能預知觀測方程和動力學方程是否含有系統誤差，于是，可采用移動窗口的系統誤差進行擬合。

(4) 移動窗口的系統誤差擬合在實踐中也存在一定困難，因為預先很難確定窗口的寬度。在本次試算中，采用窗口寬度N=10。若系統誤差變化區間有較大變化，則N也相應變化。如何選取窗口的寬度是實踐中的難點，一般需通過多次試驗經計算確定。

圖3 方案1在X，Y和Z方向位移曲線Fig.3 Displacement curve of Scheme 1 in X,Y and Z direction

圖4 方案2在X，Y和Z方向位移曲線Fig.4 Displacement curve of Scheme 2 in X,Y and Z direction

4 結論

(1) 在變形監測中，當邊坡的物理信息不充分時，可以把它們看作一種未知的系統誤差，利用濾波輸出的觀測殘差和狀態預報值殘差對它們進行開窗擬合，這樣就可以降低未知的系統偏差影響，從函數模型和隨機模型2個方面同時改進濾波結果的可靠性。

(2) 本文提出的算法其應用前提是：在一個固定的時間窗口內，未知信息是1個常量。然而，在實際變形觀測中，未知的信息會不斷變化，因此，該解算方法還有待于進一步研究。

[1] Zangerl C, Eberhardt E, Perzlmaier S. Kinematic behaviour and velocity characteristics of a complex deep-seated crystalline rockslide system in relation to its interaction with a dam reservoir[J]. Engineering Geology, 2010, 112: 53-67.

[2] Bonzanigo L, Eberhardt E, Loew S. Long-term investigation of a deep-seated creeping landslide in crystalline rock-geological and hydromechanical factors controlling the campo vallemaggia landslide[J]. Canadian Geotechnical Journal, 2007, 44(10):1157-1180.

[3] 朱建軍, 丁曉利, 陳永奇. 集成地質、力學信息和監測數據的滑坡動態模型[J]. 測繪學報, 2003, 32(3): 261-266.

ZHU Jian-jun, DING Xiao-li, CHEN Yong-qi. Dynamic landsliding model with integration of monitoring information and mechanic information[J]. Acta Geodaetica et Cartographica Sinca, 2003, 32(3): 261-266.

[4] YANG Yuan-xi, ZENG An-min. Adaptive filtering for deformation parameter estimation in consideration of geometrical models[J]. Science in China Series D: Earth Science,2009, 52(8): 1216-1222.

[5] Shi G H. Applications of discontinuous deformation analysis(DDA) to rock engineering[J]. Computtional Mechanics, 2009(2):136-147.

[6] Bonaldi P. Displacement forecasting for concrete dams via deterministic mathematical models[J]. Water Power & Dam

Construction, 1977, 29(9): 74-78.

[7] Purer E. Application of statistical methods in monitoring dam behavior[J]. Water Power & Dam Construction, 1986, 38(12):16-19.

[8] DeSortis A, Paoliani P. Statistical analysis and structural identification in concrete dam monitoring[J]. Engineering Structures, 2007, 29: 110-120.

[9] Schwintzer P. Generalization for deformation vector with hybrid model[C]//Joó I, Detrek?i A, eds. Deformation Measurements.Budapest: Akademiai kiadó, 1982: 453-463.

[10] Bock Y. Estimating crustal deformations from a combination of baseline measurements and geophysical models[J]. Bull Geod,1983, 57: 294-311.

[11] Bock Y, Schaffrin B. Robust predication of the Earth’s crustal movements from precise geodetic data and a vague geophysical mode[C]//The First World Congress of Bernoulli Society on Mathematical Statistics. Taschkent (USSR), 1986 361-367.

[12] Segall P, Matthews M V. Displacement calculations from geodetic data and the testing of geophysical deformation model[J]. J Geophys Res, 1988, 93(B12): 14954-14966.

[13] 楊元喜, 張雙成. 導航解算中的系統誤差及其協方差矩陣擬合[J]. 測繪學報, 2004, 33(3): 189-194.

YANG Yuan-xi, ZHANG Shuang-cheng. Fittings of systematic errors and covariance matrices in navigation[J]. Acta Geodaetica et Cartographica Sinca, 2004, 33(3): 189-194.

[14] Lü W C, Xu S Q. Kalman filtering algorithm research for the deformation information series of the similar single difference model[J]. Journal of China University of Mining and Technology,2004, 14(2): 189-194.