基于流固耦合特性的非飽和膨脹土變形仿真計算

范臻輝，張春順，肖宏彬

(1. 中南大學 土木建筑學院，湖南 長沙，410075；2. 悉尼大學 巖土工程研究中心，澳大利亞 悉尼，2006；3. 中南林業科技大學 土木工程與力學學院，湖南 長沙，410004)

對于大多數工程來說，將土當作飽和土是一種合理的簡化，但是，對于某些特殊區域或特殊性質的土，這種簡化將造成理論研究結果與實際結果存在誤差。如在膨脹土地基基礎的設計中，若單純按照膨脹土的現有強度進行設計，則有可能將強度參數估計過高，導致工程不安全[1]；若按其最低強度進行設計，又將造成浪費[2]。因此，需合理地提出膨脹土在不同狀態下的強度參數，這是工程的客觀需要[3-4]。此外，膨脹土等非飽和土的變形性能也隨飽和度的變化而變化[5-6]。這些問題都是飽和土力學難以解決的。按非飽和狀態研究膨脹土的工程力學性質是土力學發展的趨勢[7]。在非飽和膨脹土的本構模型研究方面，Gens和Alonso提出了一個非飽和膨脹土彈塑性概念模型(G-A模型)[8]。該模型以Alonso的一般非飽和土彈塑性模型為基礎，從分析膨脹的微觀機理出發，反映了膨脹土的濕脹干縮變形特性，但將土體變形分為微觀和宏觀2個結構層次進行計算，所建模型非常復雜。許多學者先后對G-A模型進行了簡化和改進，取得較好的研究成果[9-12]，但這些研究側重于非飽和膨脹土的應力-應變本構關系。膨脹土吸水膨脹、失水收縮等問題需考慮水、氣兩相流體流動和固相變形之間的相互作用，因此，研究非飽和膨脹土流-固耦合問題具有重大理論和實際意義。在此，本文作者按照沈珠江[13]提出的思路，并借用Alonso提出的BBM模型推導過程建立非飽和膨脹土的彈塑性本構模型的矩陣表達式，并選用適用的土-水特征曲線方程和非飽和土滲透系數方程，構建完整的非飽和膨脹土滲流-變形耦合分析模型，以便更加準確地分析膨脹土的膨脹收縮變形，進一步評價膨脹土工程特性。

1 非飽和膨脹土本構模型

1.1 應力狀態變量的選擇與有效應力原理

Bishop較早提出了非飽和土的有效應力公式。假定作用于非飽和土的外應力是由非飽和土骨架、孔隙水和孔隙氣共同承擔。在外應力σ作用下，根據土粒間靜力平衡原理可得Bishop有效應力公式：

式中：σ′為土體有效應力；ua為孔隙氣壓力；uw為孔隙水壓力；χ為有效應力參數， χ = Aw/A，其值介于0～1.0之間；A為剪切面面積；Aw為孔隙水面積。

從式(1)可以看出：要確定σ′，必須首先知道χ。χ一直是人們對非飽和土問題研究的重點，幾十年來，人們提出的方法和得到χ的形式多種多樣[14]。在某些情況下，用飽和度Sr描述有效應力參數χ更方便。本文采用單變量理論來描述非飽和土體的應力狀態，并令)(rSφχ=，則式(1)可改寫為：

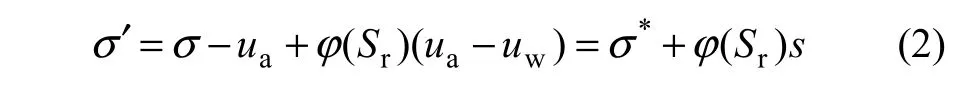
式中：wauus -= ，為基質吸力；Sr為土體飽和度。

1.2 土-水特征曲線

土-水特征曲線又稱水分特征曲線，是表示非飽和土的基質吸力與含水質量分數、含水體積分數、飽和度或有效飽和度之間的關系曲線。對于非飽和土，土-水特征曲線的數學模型并不是唯一的。土的類型不同，所得出的數學模型也有所不同，且大部分用于描述土-水特征曲線的數學模型都是根據經驗、土體結構特征和曲線的形狀而建立的。戚國慶等[15]采取基質吸力的冪函數多項式形式，建立了非飽和土-水特征曲線的通用數學模型：

應用式(3)對非飽和膨脹土體基質吸力與含水量或飽和度的關系進行擬合得到相關系數，簡單易行，一般由三次項就能達到很高精度。

1.3 非飽和土的滲透系數

對于飽和土，不論在穩定或非穩定滲流條件下，都認為土的滲透系數是保持不變的常量。而非飽和土的情況較復雜，非飽和土的滲透系數除與土體的種類、土體孔隙狀態、流體的性質有關外，還與土體飽和程度或者土的基質吸力密切相關。非飽和土體的滲透系數往往小于飽和土體的滲透系數，滲透系數不是常數，是隨飽和度和水的體積分數的變化而變化的。飽和度和水的體積分數的變化往往引起基質吸力的變化，因此，非飽和土的滲透系數常常表征為飽和度、水的體積分數或基質吸力的函數。

Gardner提出非飽和土滲透系數的計算公式[16]：

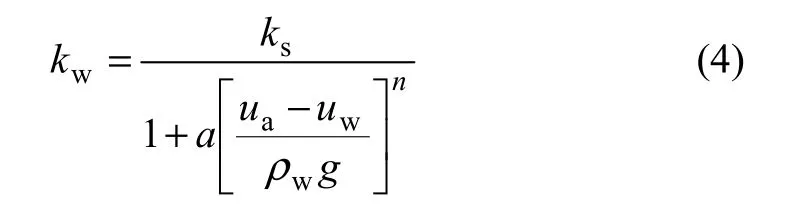
式中：a和n為試驗參數；kw為非飽和土的滲透系數；ks為這種土在飽和時的滲透系數；wρ為水的密度。式(4)物理概念比較明確，是比較常用的表達式。

1.4 非飽和膨脹土本構模型的建立

沈珠江[13]認為當有效應力原理適用時，任何一個飽和土本構模型都可方便地推廣到非飽和土上，只需把飽和土的有效應力公式σ′=σ-uw換成即可。其中：

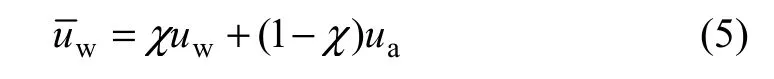
按照沈珠江的思路，將修正劍橋模型中的有效應力進行代換，采用相關聯流動法則，可以得到：

式中：f為屈服條件；g為塑性勢函數；p′為有效平均主應力，；M為其飽和土的極限線斜率；p0為土體屈服強度，隨基質吸力變化而變化。

式中： pc為參考應力； p*為飽和土的先期固結壓力；κ為回彈指數；λ(0)為飽和情況下對于應力的壓縮指數；λ為非飽和土相對于壓應力p的壓縮系數，隨基質吸力的變化而變化。

式中：r為常數， r = λ (s →∞)/λ(0)；β為控制λ隨s增長速率的參數。

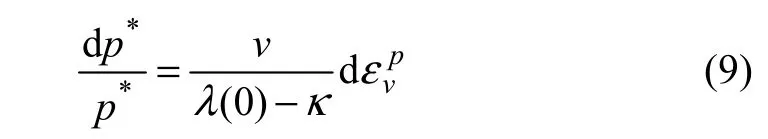
1.5 非飽和膨脹土彈塑性本構模型的矩陣表達式

在一般情況下，假定非飽和膨脹土中排氣通道暢通。由于排氣速度遠大于排水速度，因此，可以忽略排氣過程，即假定各處氣壓力均等于大氣壓。當孔隙氣壓力保持不變時，可采用負孔隙水壓力代替基質吸力[17]，將式(2)中的基質吸力采用負孔隙水壓力代替，并采用矩陣形式可表示為：

由式(6)，(7)和(9)可知：屈服函數和塑性勢函數是有效應力σ、孔隙水壓力wu (基質吸力)、硬化參數*p的函數。

根據流動法則，各應力狀態點的塑性應變增量方向與通過該點的塑性勢面相垂直，且塑性應變為：

式中：dλ為非負的標量乘子；dεp為塑性應變增量矩陣；為塑性體應變增量矩陣。

由應力應變的增量關系可知：

式中：eD為彈性剛度矩陣；edε為彈性應變增量；εd為總應變增量。

對屈服面上的應力狀態，根據式(12)，有：

組合式(9)，(14)，(15)和(17)得：

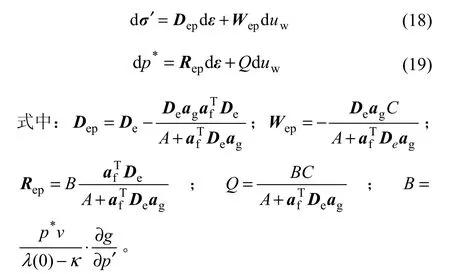
注意到epW 為列向量，epR 為行向量，將孔隙水壓力(或吸力)增量作為1個附加的應變增量，可得：

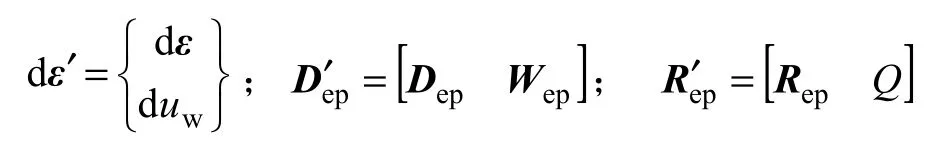
則本構方程式(18)和(19)可以轉換為：

2 非飽和膨脹土流-固耦合分析

2.1 基本假設

分析非飽和膨脹土流-固耦合有限元時，采用如下假設：(1) 土體為均質各向同性材料；(2) 土骨架只有微小應變；(3) 土顆粒和孔隙水不可壓縮；(4) 土顆粒和孔隙水變形不受溫度的影響；(5) 孔隙水和氣各自連通，孔隙水運動服從Darcy定律，而孔隙氣壓力假定為0 Pa。

2.2 控制方程

2.2.1 平衡方程

土體三維的平衡方程可以寫成如下的緊湊形式：

應用Green-Gauss定理和Galerkin加權殘值法，由式(22)可得：

式中： Ve為單元體積； Se為單元表面積；，為外表面張力向量； B 和 N 分別uu為應變-位移形函數和位移形函數；U為節點位移向量；變量上帶一點“·”表示該變量對時間的導數。由式(11)和(18)可得：

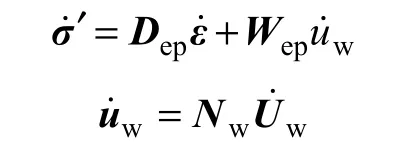
其中：wU 為節點孔隙水壓力(或基質吸力)向量；wN為孔隙水壓力(或基質吸力)的形函數。

將單元矩陣組集起來形成總體矩陣：

2.2.2 連續方程

根據孔隙流體質量平衡，可以導出流體的連續方程：

式中：wρ為孔隙流體的密度；v孔隙流體的流速向量。因為

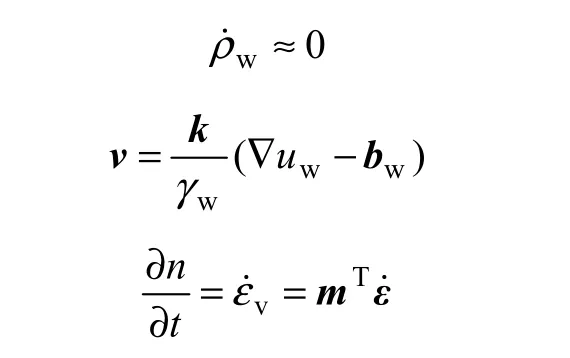
故可以將式(25)轉換為：

對式(26)，在空間離散 uw，并應用 Green-Gauss定理和Galerkin加權殘值法，與平衡方程類似，組集成整體矩陣為：

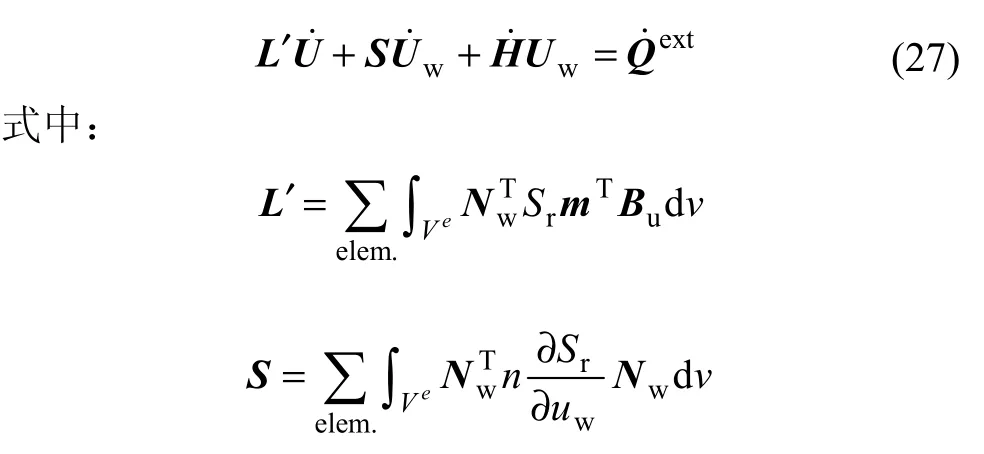
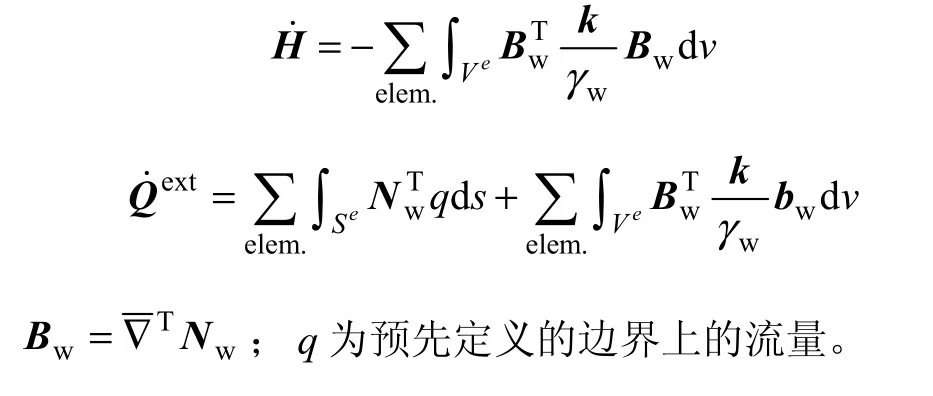
由式(24)和(27)構成了非飽和膨脹土流-固耦合分析的控制方程：見圖2。

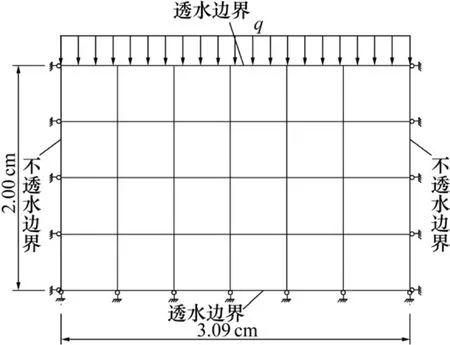
圖1 計算模型網格劃分Fig.1 Mesh of model

2.3 流-固耦合有限元數值解法

對式(28a)和(28b)，采用交替解法求解。其基本思路是：首先將問題在時域上進行離散；求解其中一組方程組(如平衡方程)，將求得的結果代入另一組方程組中(如連續方程)求解，再將所得結果回代到前一組方程組中；若2次求得的值相差較大，不能滿足誤差要求，則重復以上步驟，直到滿足要求為止；然后，按上述思路繼續求解下一時步。

3 算例分析

據文獻[18]進行有荷膨脹試驗。該土樣浸水前高為2.00 cm，直徑為6.18cm，初始含水量w=20.77%，初始干密度ρd=1.76 g/cm3，垂直壓力q為25 kPa。采用軸對稱模型，計算參數如下：A0=1.019 42，A1=0.067 996 MPa-1，A2=-13.471 64 MPa-2，A3= -23.375 64 MPa-3，a=10-5，n=3.0，ks=10-9m·s-1，M=0.8，λ(0)=0.25，κ=0.05，pc=1 MPa，p*=0.1 MPa，r=0.75，β=12 MPa-1，E=5 MPa，μ=0.3。計算模型網格劃分見圖1。

整個計算分為3個階段：第1階段，計算初始應力分布；第2階段，計算垂直荷載；第3階段，計算浸水膨脹率。其中，第3階段浸水膨脹率的計算結果見圖2。

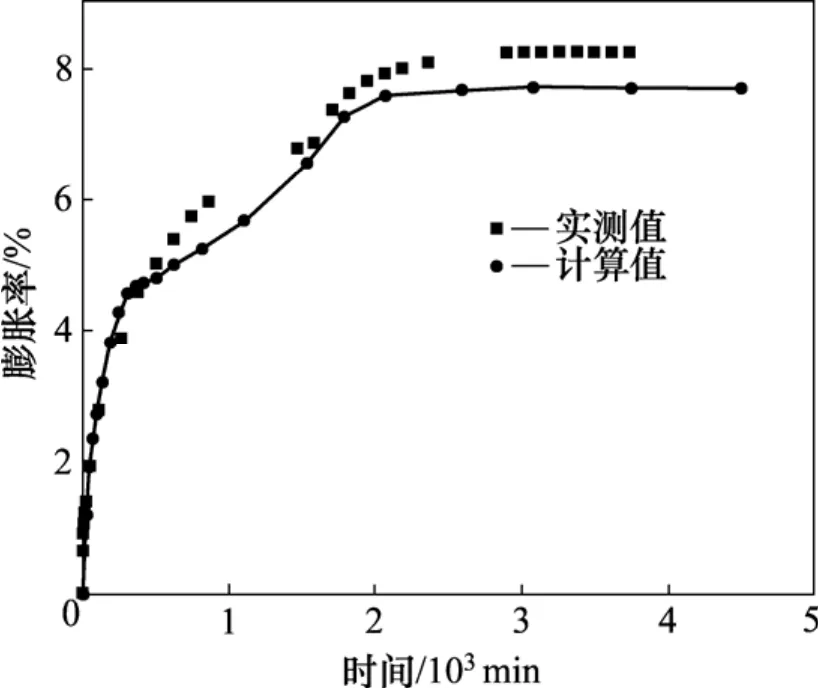
圖2 膨脹率隨時間的變化曲線Fig.2 Relationship between percent swell and time

從圖2可以看出：采用本文程序所得的計算值與實測值較吻合，尤其在浸水變形的前期階段，吻合程度更大。可見：采用本文所編制的程序能較好地模擬膨脹土膨脹變形。

圖3所示為各時刻膨脹土樣的飽和度等值線圖，圖4所示為各時刻膨脹土樣的孔隙水壓力等值線圖。

從圖3和圖4可以看出：由于土樣是從底部浸水，土樣底部的飽和度比上部的大，同樣，土樣底部的孔隙水壓力比上部的大，隨著時間的增加，水慢慢滲入，土樣飽和度逐漸增加，孔隙水壓力也逐漸增大，由負孔隙水壓力(非飽和狀態)變為正孔隙水壓力(飽和狀態)；到第3 741 min時，土樣已處于飽和狀態，土體的孔隙水壓力也全部為正，這時不會再有水分進入土體，土體處于穩定狀態，其膨脹變形也趨于穩定，這一點從圖2也可以得到驗證。

圖3 各時刻點飽和度等值線Fig.3 Contour map of saturation degree axial

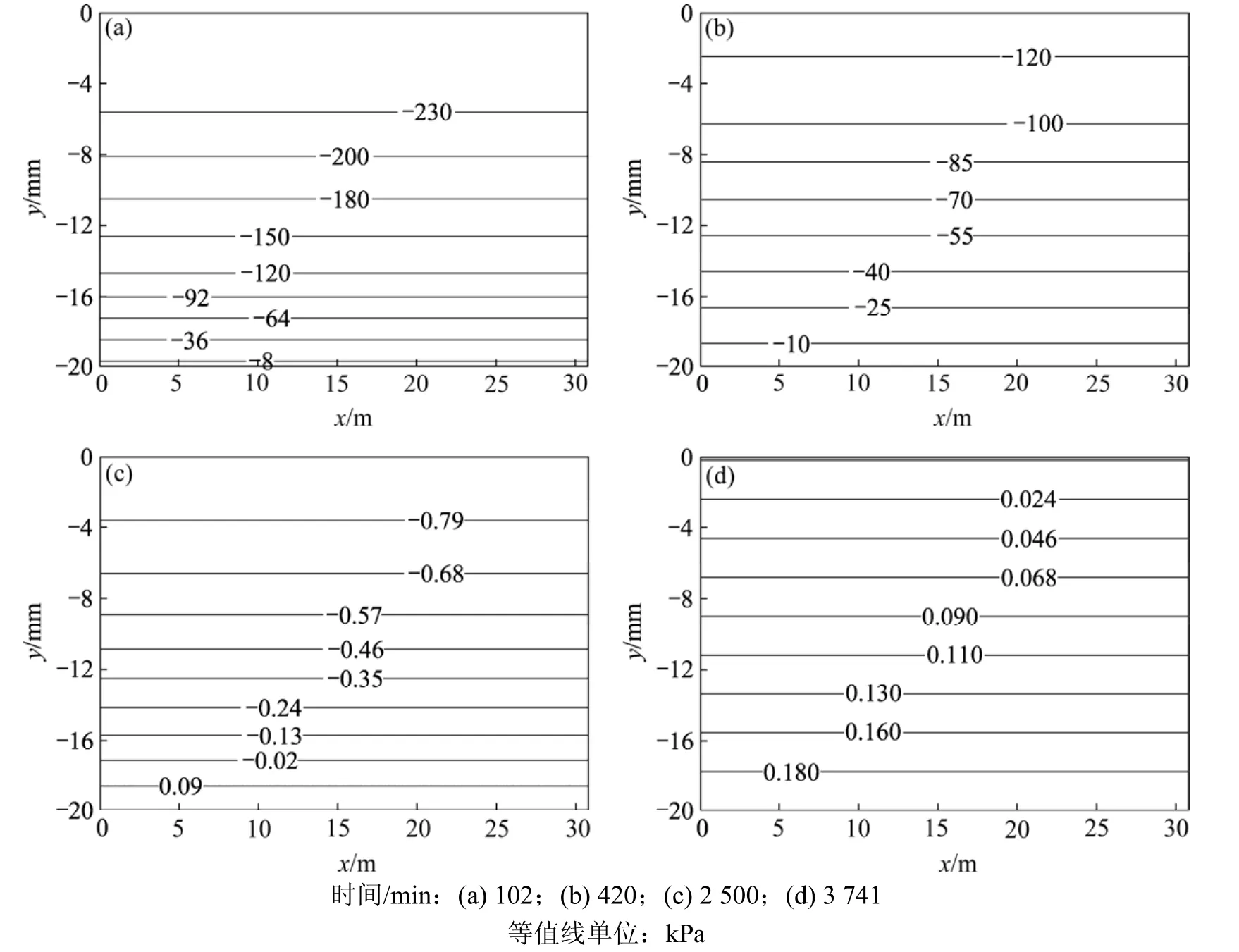
圖4 各時刻點孔隙水壓力等值線Fig.4 Contour maps of pore water pressure axial

4 結論

(1) 選擇基于有效應力原理的單變量理論作為分析依據，推導出非飽和膨脹土的彈塑性本構模型的表達式，并建立了矩陣表達式。在該矩陣表達式中，孔隙水壓力(或吸力)增量作為 1個附加的應變增量，可以通過設置邊界孔隙水壓(或基質吸力)的變化來模擬膨脹土體的吸水和失水。

(2) 在選用適用的土-水特征曲線方程和非飽和土滲透系數方程的基礎上，根據流-固耦合力學的理論與方法，將膨脹土吸水膨脹或失水收縮過程視為一個動態耦合作用過程，建立了滲流-變形耦合模型。該模型可以計算飽和和非飽和土體的滲流與固結，考慮了流-固耦合作用引起的孔隙比和滲透系數變化(包括有效應力的影響)。室內有荷膨脹試驗模擬結果驗證了模型的可靠性和適用性。

[1] 董隴軍, 李夕兵, 宮鳳強. 膨脹土脹縮等級分類的未確知均值聚類方法及應用[J]. 中南大學學報: 自然科學版, 2008,39(5): 1075-1080.

DONG Long-jun, LI Xi-bing, GONG Feng-qiang. Unascertained average clustering method for classification of grade of shrink and expansion for expansive soils and its application[J]. Journal of Central South University: Science and Technology, 2008,39(5): 1075-1080.

[2] FAN Zhen-hui, WANG Yong-he, XIAO Hong-bin. Analytical method of load-transfer of single pile under expansive soil swelling[J]. Journal of Central South University of Technology,2007, 14(4): 575-579.

[3] XIAO Hong-bin, ZHANG Chun-shun, HE Jie, et al. Expansive soil-structure interaction and its sensitive analysis[J]. Journal of Central South University of Technology, 2007, 14(3): 425-430.

[4] 詹良通, 吳宏偉. 吸力對非飽和膨脹土抗剪強度及剪脹特性的影響[J]. 巖土工程學報, 2007, 29(1): 82-87.

[5] ZHAN Liang-tong, WU Hong-wei. Effect of suction on shear strength and dilatancy of an unsaturated expansive clay[J].Chinese Journal of Geotechnical Engineering, 2007, 29(1):82-87.

[6] 韓華強, 陳生水, 鄭澄鋒. 非飽和膨脹土強度及變形特性試驗研究[J]. 巖土工程學報, 2008, 30(12): 1872-1876.

HAN Hua-qiang, CHEN Sheng-shui, ZHENG Cheng-feng.Experimental study on strength and deformation of unsaturated expansive soils[J]. Chinese Journal of Geotechnical Engineering,2008, 30(12): 1872-1876.

[7] 范臻輝, 王永和, 肖宏彬. 南寧膨脹土膨脹變形規律的試驗與應用研究[J]. 鐵道學報, 2007, 29(1): 86-89.

FAN Zhen-hui, WANG Yong-he, XIAO Hong-bin. Experimental and applied research on swelling laws of nanning expansive soil[J]. Journal of the China Railway Society, 2007, 29(1):86-89.

[8] 殷宗澤. 土力學學科發展的現狀與展望[J]. 河海大學學報,1999, 27(1): 1-5.

YIN Zong-ze. Status and prospects of soil mechanics development[J]. Journal of Hohai University, 1999, 27(1): 1-5.

[9] Gens A, Alonso E E. A framework for the behavior of unsaturated expansive clays[J]. Ganadian Geotechnique Journal,1992, 29: 1013-1032.

[10] 盧再華, 王權民, 陳正漢. 非飽和膨脹土本構模型的試驗研究及分析[J]. 地下空間, 2001, 21(5): 379-385.

LU Zai-hua, WANG quan-min, CHEN Zheng-han. Research on the constitutive model of unsaturated expansive soil[J].Underground Space, 2001, 21(5): 379-385.

[11] 盧再華, 陳正漢. 非飽和原狀膨脹土的彈塑性損傷本構模型研究[J]. 巖土工程學報, 2003, 25(4): 422-426.

LU Zai-hua, CHEN Zheng-han. An elastoplastic damage constitutive model of unsaturated undisturbed expansive soil[J].Chinese Journal of Geotechnical Engineering, 2003, 25(4):422-426.

[12] 姚志華, 陳正漢, 黃雪峰, 等. 結構損傷對膨脹土屈服特性的影響[J]. 巖石力學與工程學報, 2010, 29(7): 1503-1512.

YAO Zhi-hua, CHEN Zheng-han, HUANG Xue-feng, et al.Influence of structural damage on yielding characteristics of expansive soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1503-1512.

[13] 沈珠江. 非飽和土力學實用化之路探索[J]. 巖土工程學報,2006, 28(2): 256-259.

SHEN Zhu-jiang. Exploitation of practical use of unsaturated soil mechanics[J]. Chinese Journal of Geotechnical Engineering,2006, 28(2): 256-259.

[14] 邢義川, 謝定義, 李振. 非飽和土的有效應力參數研究[J]. 水利學報, 2000, 31(12): 77-81.

XING Yi-chuan, XIE ding-yi, LI Zhen. Study on effective stress parameter of unsaturated soi[J].Journal of Hydraulic Engineering,2000, 31(12): 77-81.

[15] 戚國慶, 黃潤秋. 土水特征曲線的通用數學模型研究[J]. 工程地質學報, 2004, 12(2): 182-186.

QI Guo-qing, HUANG Run-qiu. An universal mathematical model of soil-water characteristic curve[J]. Journal of Engineering Geology, 2004, 12(2): 182-186.

[16] Desai C S, Christian J T. Numerical Methods in Geotechnical Engineering[M]. New York: McGraw Hill Book Co, 1977:307-329.

[17] Sheng D, Sloan S W, Gens A, Smith D W. Finite element formulation and algorithms for unsaturated soils, Part I:Theory[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27: 745-765.

[18] 范臻輝. 膨脹土地基脹縮特性及樁-土相互作用研究[D]. 長沙: 中南大學土木建筑學院, 2007: 26-43.

FAN Zhen-hui. Research on swelling-shrinking characteristic and pile-soil interaction of expansive soil foundation[D].Changsha: Central South University. School of Civil Engineering and Architecture, 2007: 26-43.