無轉速計的旋轉機械Vold-Kalman階比跟蹤研究

鄧 蕾，傅煒娜，董紹江，湯寶平

(重慶大學 機械傳動國家重點實驗室，重慶 400030)

階比跟蹤(OT)技術是旋轉機械升降速過程非平穩振動信號分析的有效方法，在旋轉機械的非平穩振動信號分析和故障診斷中占有重要地位。

1993年Vold和Leuridan［1］首次提出了基于卡爾曼濾波的階比跟蹤的方法，開創了通過時域濾波方法進行階比跟蹤的新思維。目前，丹麥的B＆K公司將VKF-OT方法作為其階比分析商業化軟件的主要技術，并得到了廣泛的應用。文獻［2］對VKF-OT理論作了進一步的詳細研究，提出了角速度和角位移兩種VKFOT方法，對兩者之間的區別進行了詳細地描述。在此基礎上文獻［3］提出和實現了自適應VKF-OT方法。另外，國內對此也作了一些研究［4，5］。

然而，VKF-OT方法仍需要通過安裝轉速計來獲取轉速信號，在不方便安裝鑒相裝置的場合限制了應用。針對簡化階比跟蹤的實現途徑和對硬件安裝要求的問題，文獻［6］提出了基于短時傅里葉變換的峰值估計瞬時頻率的階比跟蹤方法，結合Gabor時頻濾波實現了階比分量的提取。文獻［7］提出了基于STFT-VA瞬時頻率估計的自適應VKF-OT方法。但這些方法主要是在旋轉機械振動信號的時頻譜圖中通過峰值搜索獲得某階比分量的瞬時頻率，進而得到所需要的參考軸轉速，所以分析精度受到頻率分辨率的限制，只有在特定條件下才能應用于多分量信號。

本文從瞬時頻率估計理論出發，結合離散頻譜校正技術中的能量重心法，通過研究兩者之間的聯系，改進了瞬時頻率估計方法，再將其應用于VKF-OT方法中，提出了一種無轉速計的基于能量重心法瞬時頻率估計的VKF-OT方法。

1 Vold-Kalman階比跟蹤原理

階比定義為參考軸每轉內發生的旋轉振動次數，可以設定為一個幅值和頻率隨時間變化的正弦函數，階比的頻率和參考軸的旋轉頻率相關聯。階比信號可以表示為幅值和載波的乘積［4］:

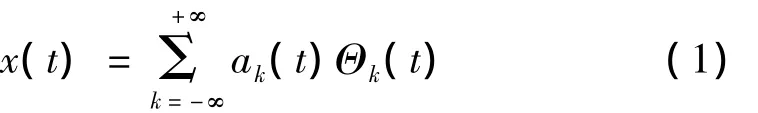
式中，k為基本頻率或參考軸轉速的倍數，表示為被跟蹤的階比;ak(t)表示復包絡，代表了階比幅值的變化，a－k(t)是 ak(t)的復共軛 ak(t)=a－k(t)*。Θk(t)為載波，表示為:

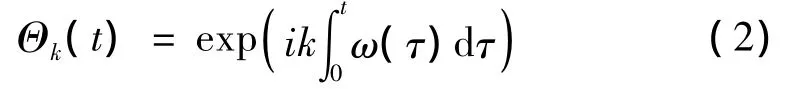
式中，ω(τ)為參考軸的角頻率，∫t0ω(τ)dτ 為角位移。式(2)的離散形式表示為:

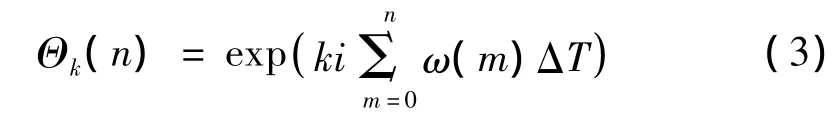
VKF-OT的主要目標是獲得復包絡ak(t)或者離散形式的ak(n)

由式(1)知，復包絡ak(t)是載波Θk(t)的低頻幅值調制，由于系統的固有慣量，使得階比幅值平滑變化，可以用低階多項式表示，則系統的狀態方程為:

式中，▽表示不同的算子，s為給定階數，ε(n)為非一致項。

實際測得的振動信號y(n)由各階比分量xk(n)的總和加上測量誤差和噪聲ξ(n)組成，則系統的觀測方程為:

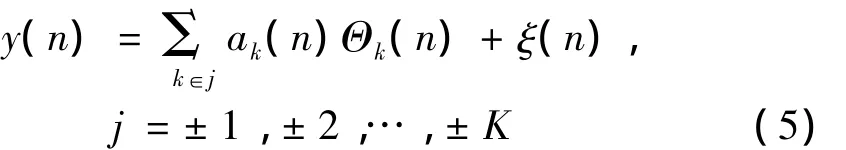
為了跟蹤某一階比分量xk(n)，用VKF-OT方法來計算復包絡ak(n)，則狀態方程和觀測方程給出以下形式:

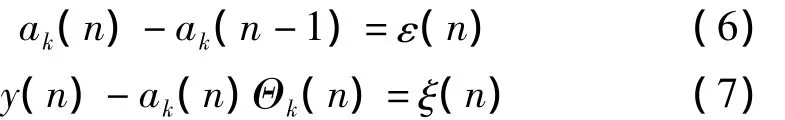
根據式(6)，展開一階狀態方程:

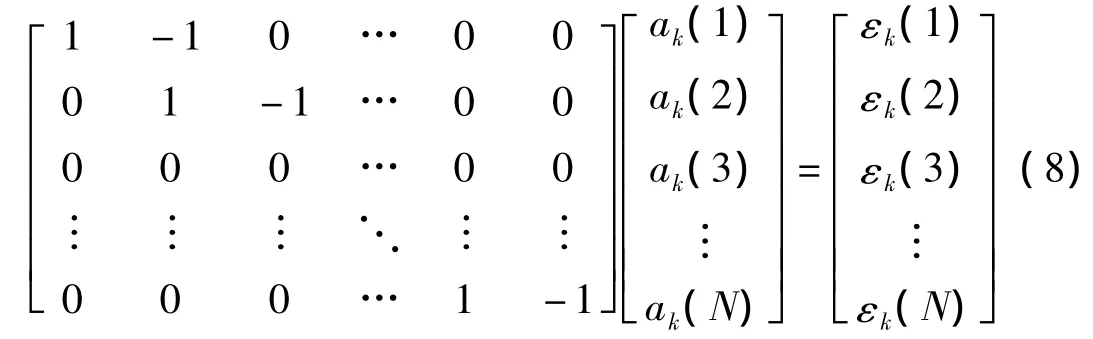
其矩陣形式為:

其中，M為N×N－1的矩陣，N為采樣點數。同樣，根據式(7)，系統的觀測方程為:

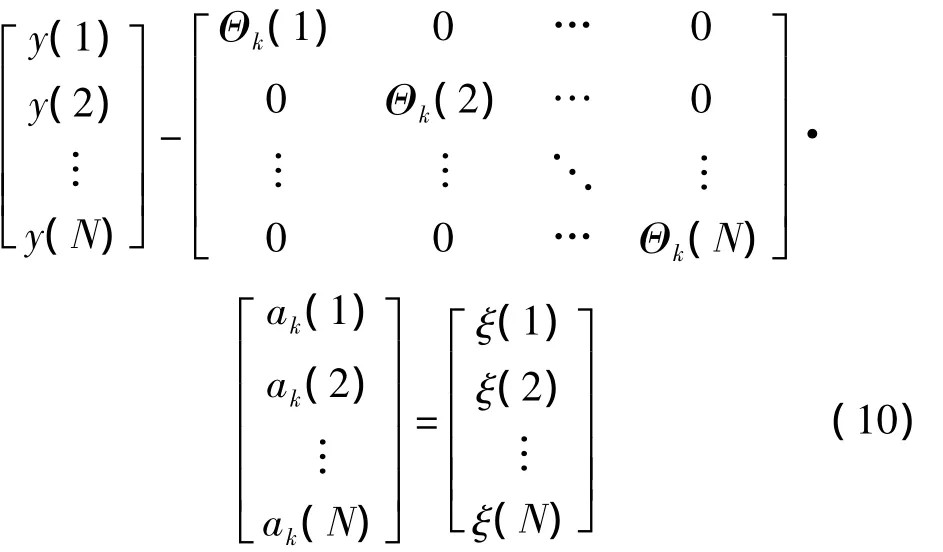
其矩陣形式為:

根據系統的狀態方程(8)和觀測方程(10)，通過最小二乘法，使得非一致相ε(n)以及測量誤差和噪聲ξ(n)的平方和最小［8］，求得未知量 ak(n)。

2 基于能量重心校正法的瞬時頻率估計

2.1 瞬時頻率原理

瞬時頻率(IF)是非平穩信號分析中的一個重要概念，Ville于1948年提出的瞬時頻率定義式是目前在學術界最為常用且得到了普遍認可［6，9］，即若實信號為s(t)=a(t)cosφ(t)，則 IF 定義為:

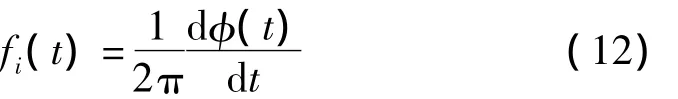
另一種等價形式為時頻分布(TFD)的一階矩，即:

2.2 能量重心離散頻譜校正法

能量重心校正法是由三點卷積幅值校正法發展起來的。該方法可以同時對離散頻譜的頻率、幅值和相位進行校正［10］。能量重心法是通過利用各種窗函數離散頻譜的能量重心無窮逼近坐標原點的特點進行離散頻譜校正的。這種方法在分析平穩或準平穩信號時，具有較高的分析精度。

設Gi為加Hanning窗的諧波信號的功率譜第i條譜線值，Gk為主瓣內譜線最大值，k為幅值最大點對應的譜線號，采樣頻率為fs，采樣點數為N，f0為主瓣中心，得到能量校正法校正頻率的通用公式:

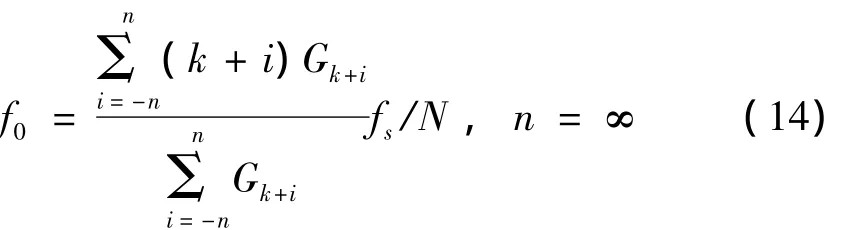
根據帕賽瓦定理，設能量恢復系數為Kt，則校正后的幅值為:

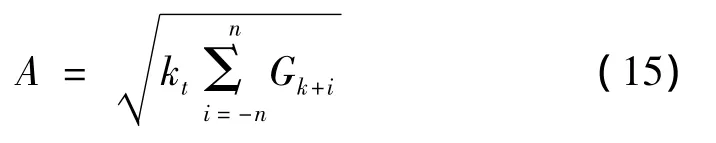
離散頻率校正方法中的能量法對所有對稱窗函數都適合，校正精度與窗函數有關，加Hanning窗時具有較高的校正精度。負頻率成分和間隔較近的多頻率成分產生的干涉現象所帶來的誤差對精度的影響小。不考慮信號中噪聲的影響，是一種精度較高的近似校正方法。

2.3 基于能量重心法的瞬時頻率估計(IFE)的原理

在STFT時頻面上進行峰值搜索估計瞬時頻率是目前獲取旋轉機械升降速階段振動信號的瞬時頻率的主要方法［6］。但是這種方法的估計精度依賴于頻率分辨率，鄰近頻率成分的干擾也會對估計精度產生影響，存在時頻集聚性不是很理想的問題。另外，在求取多分量信號的IF時，一般通過時頻濾波將其它分量遮掩，提取某一分量的IF，依次遞推，增加了算法的計算量。

離散頻譜校正方法可以改善由于時域截斷產生的能量泄漏的問題，提高分析精度。而旋轉機械升降速過程的振動信號屬于非平穩信號，不能直接使用離散頻譜校正方法。因此，根據STFT算法原理，把短時間間隔的信號看成是準平穩信號，就能夠利用離散頻譜校正方法來校正信號的頻譜。這樣可以在頻域中直接通過振動信號的頻譜進行瞬時頻率估計，并通過離散頻譜校正方法提高分析精度，進而實現階比跟蹤。

比較式(13)和式(14)發現:式(14)是式(13)的近似離散表達形式，也就是說通過能量重心法校正獲得的頻率近似等于瞬時頻率。基于能量重心法IFE的基本思路是根據假定的瞬時頻率初始值進行整周期采樣，同時做加窗的DFT;然后利用能量重心法對該段信號做離散頻譜校正，得到新的瞬時頻率;依次迭代重復，最后得到準確的瞬時頻率值。該方法的誤差主要來自信號的截斷誤差，所以采用整周期采樣來減小誤差，同時對信號加窗，以便提高精度和減小各相鄰譜線之間的干擾。

下面給出基于能量重心法瞬時頻率估計的計算步驟。

(1)對振動信號進行分段，數據長度為L，每M個點為一段，重疊長度為 l，共分為 m段，m∈［0，Num－1］，Num=int［L/(M －1)］=int(L/dN)，式中 int表示對計算結果取整;

(2)旋轉機械升降速過程中總有一穩定轉速(相對恒定)階段，比如，最高轉速為9000 r/min的降速階段，對應的一階最大轉頻為150 Hz。所以選擇最高速階段作為初始分析段，根據最大轉頻和該段的頻譜成分設定初始轉頻f0，局部極大值搜索范圍q和整周期采樣系數K;

(3)根據當前m，計算當前分段數據的起始點位置:p=m×dN。在采樣信號中截取M點數據{s(i)}，i∈［p，M －1+p］};

(4)根據f0和系數R計算出整周期采樣點數N0，以分析段中點為中心重新選取N0點作為新的分析段，并對其做加窗的DFT，求得搜索范圍q內最大頻率譜線位置以及其左右鄰近的n條譜線的功率值。其中，n的取值與加窗的類型有關，這里加Hanning窗，n=2;

(5)利用能量重心法對搜索到的峰值頻率譜線進行頻譜校正，得到校正頻率f，令f為新的轉頻，重新計算出整周期采樣所需的采樣點數N;

(6)如果N=N0或者達到最大迭代次數j時，f為分析段中點所對應的頻率估計值，否則，f0=f，轉步驟(4);

(7)令m=m+1，返回(3)，直到m=Num－1。

最終根據迭代求得的參考軸轉頻f(m)，插值擬合后得到瞬時頻率擬合值。

3 基于能量重心法瞬時頻率估計的VKF-OT

從前面的討論可以看出，通過能量重心法得到的參考軸轉頻近似等于瞬時頻率，由此可以獲得參考軸轉速，進而實現階比跟蹤。本文方法的實現過程如圖1所示。

獲取旋轉機械升降速階段的振動信號，對該振動信號作基于能量重心法的瞬時頻率估計，獲得參考軸瞬時頻率估計值;插值擬合后得到連續的參考軸瞬時頻率，并對各個振動采樣點進行階比相位估計;然后，設置加權因子r，選取階次p等參數，進行Vold-Kalman自適應濾波;最后得到所提取的第p階信號分量。

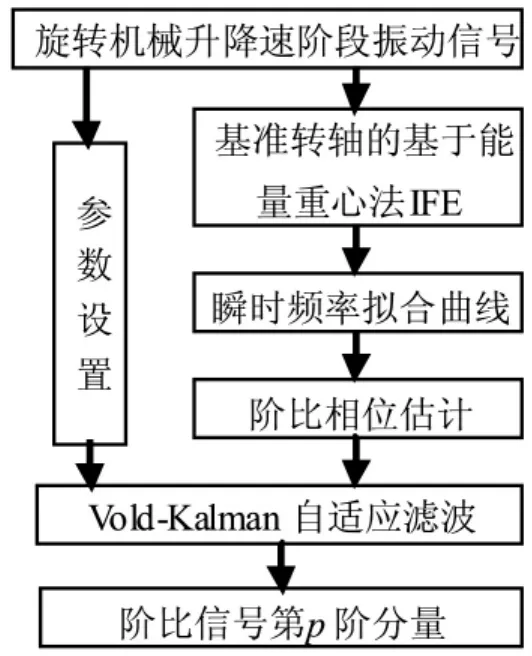
圖1 基于能量重心法的瞬時頻率VKF-OT流程圖Fig.1 Flow diagram of VKF-OT based on the improved IFE with energy centrobaric method

4 仿真與應用實例分析

4.1 仿真分析

為了驗證算法，設計一個包含兩個獨立參考軸轉速信號的仿真信號來模擬旋轉機械升速階段的振動信號。采樣點數N=10 k，采樣頻率fs=1 kHz。仿真信號的時域波形如圖2所示。

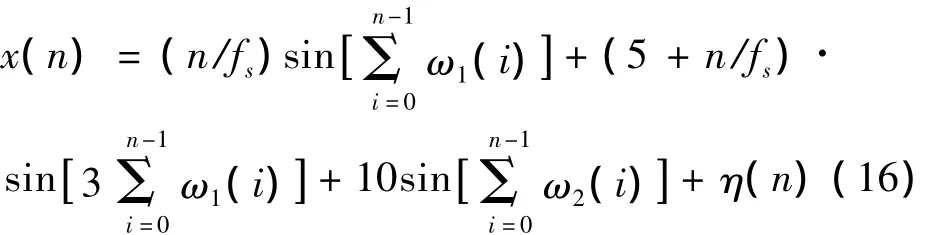
式中，η(n)為高斯白噪聲［η(n)～N(0，1)］。此仿真信號由兩組信號分量組成，第Ⅰ組包含第1階、第3階分量，基準頻率從15 Hz到150 Hz線性變化，·Δt表示第n個采樣時刻第Ⅰ轉軸轉過的相位角。第1、3階比分量的幅值分別呈0到10和5到15線性變化。第Ⅱ組為添加了高斯白噪聲的正弦信號，旋轉頻率f2(n)固定為 200 Hz，幅值固定為 10，·Δt表示第n個采樣時刻第Ⅱ轉軸轉過的相位角。

采用基于能量重心法的瞬時頻率估計方法對仿真的振動信號進行瞬時頻率估計。分析中，加Hanning窗，n=2，相鄰兩段時移點數為500，結果如圖3所示。

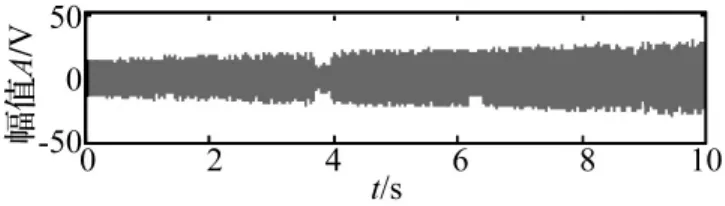
圖2 仿真信號時域波形圖Fig.2 Time waveform of synthetic signal

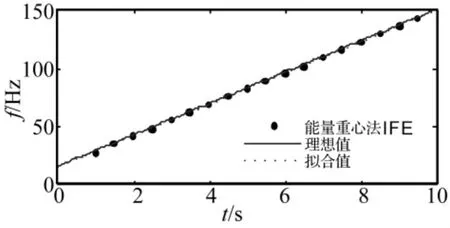
圖3 基于能量重心法的瞬時頻率估計Fig.3 IFE based on energy centrobaric method

圖3中圓點表示采用基于能量重心法的瞬時頻率估計得到的估計值，實線表示設計的參考軸Ⅰ的瞬時頻率曲線，虛線為對估計值采用插值擬合后得到的擬合曲線。從圖中可以看出，采用基于能量重心法得到的轉頻理論上近似于瞬時頻率，與仿真信號的理想值非常吻合。

分別對基于STFT峰值搜索法和本文方法獲得的瞬時頻率估計值求相對于理想瞬時頻率值的百分比誤差。

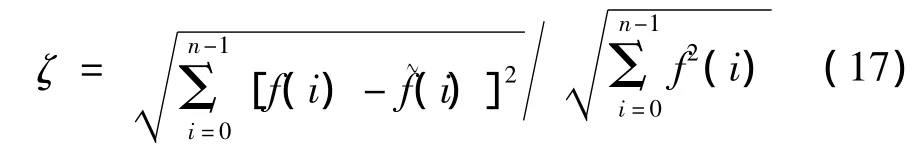
式中，f(i)為瞬時頻率的理想值，～f(i)為f(i)的擬合值，根據式(17)求得，基于STFT峰值搜索得到的瞬時頻率估計值相對于理想瞬時頻率值的百分比誤差ζ1=0.37%，基于能量重心法的瞬時頻率估計得到的擬合值相對于理想瞬時頻率值的百分比誤差ζ2=0.03%，對比結果表明，由本文提出的基于能量重心法IFE誤差小，估計的瞬時頻率逼近真實的瞬時頻率值。取移動步長為1，分別用這兩種方法計算得到瞬時頻率估計值，取某一段的數據如圖4所示。圖中結果再次說明，本文方法連續性好，分析精度受頻率分辨率的影響小。

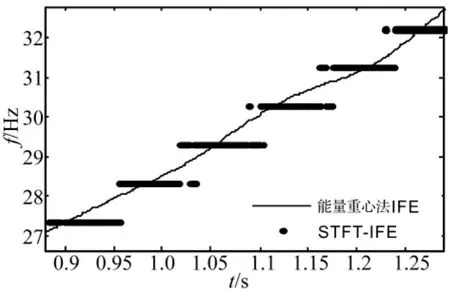
圖4 能量重心法IFE和STFT瞬時頻率估計對比Fig.4 Comparison of IFE by energy centrobaric method and STFT

然后，采用基于能量重心法IFE獲得的瞬時頻率擬合值作為參考軸對應的瞬時頻率，并求得相應的瞬時角位移信號，對振動信號進行VKF-OT分析。本方法中使用一階自適應Vold-Kalman濾波器分離各個階比分量。在圖5中，圖(a)、圖(b)分別為第Ⅰ參考軸的第1、3階比分量提取結果，圖(c)為第Ⅱ參考軸的200 Hz常頻分量提取結果。圖6為兩個軸各自階比分量的幅值，可以看出由VKF-OT分析得到的幅值與設計值相符合。

為了能夠清楚地看到提取結果與理想信號之間的差異，取第Ⅰ參考軸的第1階分量的前1000個點與設計信號進行對比。如圖7所示，實線表示用本文方法所提取的第1階比分量，虛線表示理想信號，從圖中可以看到，除了起始點處有一些偏差外，提取的階比幅值都和設計值吻合。

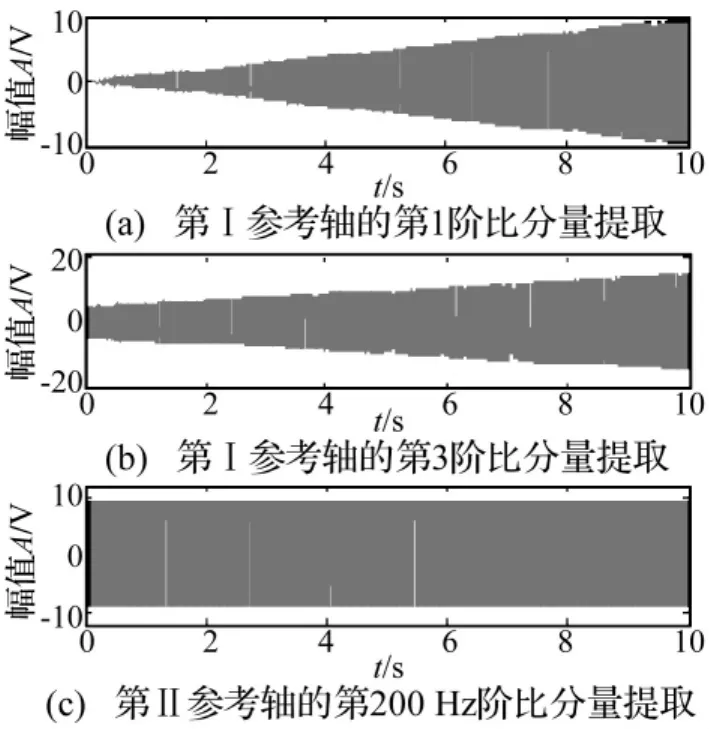
圖5 基于能量重心法瞬時頻率估計的VKF-OT各階比分量提取結果Fig.5 Extracted orders components using VKF-OT based on the improved IFE with energy centrobaric method

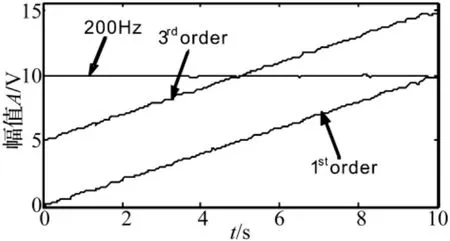
圖6 VKF-OT分析得到的Ⅰ、Ⅱ軸各階比分量幅值Fig.6 Amplitudes of orders about axes－ ⅠandⅡtracked by using VKF-OT

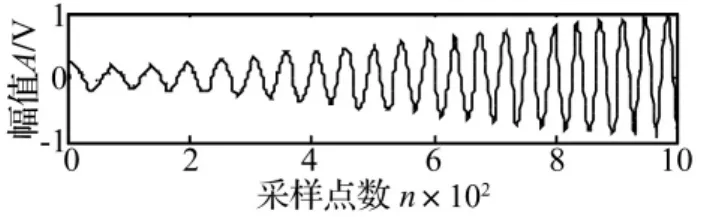
圖7 第I參考軸的第1階比分量與理想信號的前1000點對比結果Fig.7 Comparison between order－1 of axis－I and designed signal for n=1000

4.2 應用實例分析

下面對某一偏心直流電機在升速階段引起的懸臂梁結構的振動信號進行測試。試驗裝置如圖8所示，直流電機安裝在簡支梁振動臺上，振動信號用YD－37型加速計拾取。采樣頻率為10 kHz，采樣長度為75 k點。首先，通過基于能量重心離散頻譜校正法的瞬時頻率估計法提取振動信號的瞬時頻率估計值，并通過三次樣條擬合獲得瞬時頻率曲線。

圖8 電機升速振動試驗裝置Fig.8 Test setup for vibration measurement during motor's run-up

結果如圖9所示，圓點表示瞬時頻率的估計值，實線表示三次樣條插值擬合后的瞬時頻率曲線。然后，利用參考軸瞬時轉速與其瞬時頻率的對應關系，求得參考軸的轉速信號。最后，對原始振動信號進行VKFOT分析，提取第4階比分量，結果如圖10所示。分析結果表明，通過本文方法在提取振動信號瞬時頻率的同時，能夠在時域中直接提取所感興趣的某階比分量。

5 結論

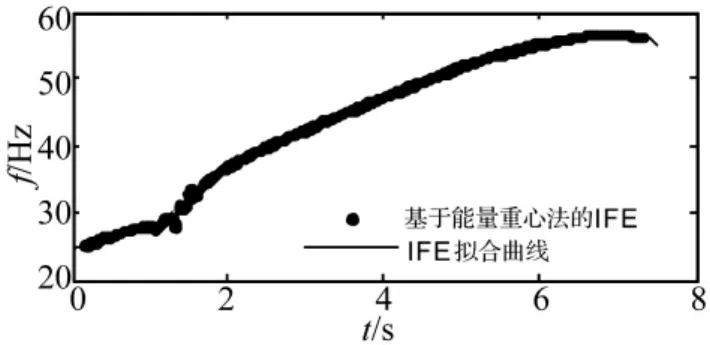
圖9 能量重心法瞬時頻率估計的結果Fig.9 IFE based on energy centrobaric method

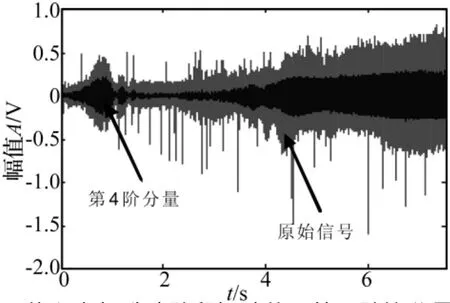
圖10 偏心電機升速階段振動信號第4階比分量提取Fig.10 Extracted order-4 waveform of motor's vibration signal

本文分析了瞬時頻率估計理論和離散頻譜校正方法中的能量重心法，根據兩者之間的理論聯系，通過用能量重心法對信號的頻譜做校正，得到了信號的瞬時頻率，再采用Vold-Kalman階比跟蹤提取感興趣的某階分量，從而實現無轉速計的旋轉機械Vold-Kalman階比跟蹤。因為該方法根據獲得的瞬時頻率對原分段信號進行了整周期采樣處理，使得頻率分辨率能夠自適應的變化，同時能量重心校正法的引入可以對誤差進行了修正，提高了分析精度并減小了各相鄰譜線之間的干擾。仿真分析和應用實例分析表明該方法的有效性，在精確提取參考軸轉速信號的同時，提取了階比分量，是對現有技術的一個有力補充。

［1］Vold H，Herlufson H，Mains M.Multi axle order tracking with the Vold-Kalman tracking filter［J］.Sound and Vibration Magazine，1997，13(5):30 －34.

［2］Pan M Ch，Lin Y F.Further exploration of Vold-Kalman filtering order tracking with shaft-speed information-I:Theoretical Part，numerical implementation and parameter investigations［J］.Mechanical Systems and Signal Processing，2006，20:1134－1154.

［3］Pan M Ch，Wu C X.Adaptive Vold-Kalman filtering order tracking［J］.Mechanical Systems and Signal Processing，2007，21:2957 －2969.

［4］孔慶鵬，宋開臣，陳 鷹.最小二乘自適應濾波旋轉機械階比跟蹤研究［J］.浙江大學學報(工學版)，2003，40(9):1648－1651.

［5］孔慶鵬，劉敬彪，章雪挺，等.多軸機械自適應濾波交叉階比跟蹤［J］.農業機械學報，2009，40(1):213－216.

［6］郭 瑜，秦樹人，湯寶平，等.基于瞬時頻率估計的旋轉機械階比跟蹤［J］.機械工程學報，2003，39(3):32－35.

［7］趙曉平，張令彌，郭勤濤.基于瞬時頻率估計的自適應Vold-Kalman階比跟蹤研究［J］.振動與沖擊，2008，27(12):112－116.

［8］Feldauer Ch，Holdrich R.Realisation of a Vold-Kalman Tracking Filter-A Least Square Problem［C］.Proceedings of the COST G-6 Conference on Digital Audio Effects(DAFX－410800)，Verona Italy，2000，December，7－9.

［9］Boashash B.Interpreting and estimating the instantaneous frequency of a signal—Part I:Fundamentals［J］.Proceedings of IEEE，1992，80(4):520－538.

［10］丁 康，江利旗.離散頻譜的能量重心校正法［J］.振動工程學報，2001，14(3):354－358.