磁流變液在平行圓盤間的擠壓流動分析

路國平，鄧國紅

(重慶理工大學重慶汽車學院，重慶 400054)

磁流變液作為一種新型的智能材料，其流變特性隨著外加磁場的變化會急劇的變化，其黏度和屈服應力可由外加磁場連續控制。基于這些特性設計出的磁流變器件具有響應速度快、能耗低、結構簡單等優點，在汽車、航空、醫療等領域都有著廣泛的應用前景。

磁流變液的工作模式有剪切［1－2］、壓力驅動［3－4］和擠壓3種。相比于剪切和驅動模式，擠壓模式的流變特性更加復雜，其相關的理論和應用研究都比較少。Alireza等［5］的研究表明磁流變液在擠壓模式下能產生很大的可控力，并首次發現了磁流變液的凝聚效應。Laun等［6］研究了具有滑移現象的牛頓流體和冪率流體的圓盤擠壓流動特性。徐春暉［7］等研究了賓漢流體的擠壓黏性力與平行剛性圓盤的滑移參數的關系。廖昌榮等［8］分析了基于圓盤擠壓模式的磁流變阻尼器的工作特性。

本文引入了臨界剪切應力，建立了新的邊界滑移模型，充分考慮磁流變液的冪率特性，建立了新的擠壓模型，并分析了磁流變液在圓盤擠壓下的流動特性，得出了擠壓力與滑移系數及冪率指數的關系，為磁流變液在擠壓模式下的應用提供了理論依據。

1 理論模型的確立

1.1 擠壓模型

磁流變液在圓盤間的擠壓流動模型如圖1所示，半徑為R的2個平行的同軸圓盤，在擠壓力作用下分別沿Z方向相向運動，并且擠壓圓盤間的磁流變液。兩盤間距為H(H=2h，且H?R)。由于磁流變液可被認為是不可壓縮的流體，所以流體質點的密度ρ在流動中保持不變，即流體的運動滿足質量守恒定律。由雷諾輸運方程，可得

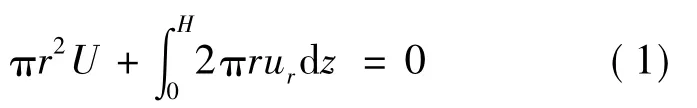
連續方程可簡化為▽·U=0，即

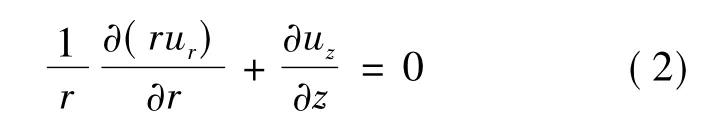
假設擠壓速度U比較小，流動可假定為定常流動，擠壓流問題可看作小雷諾數的蠕流問題。非定常項和對流項都是可忽略的高階小量，而且z方向的壓力梯度為零。則Navier-Stokes方程可近似為

對于磁流變液擠壓流的本構關系的表達，原有的模型都忽略了它的剪切稀化或增稠現象。但清華大學的田煜等［5］用實驗的手段發現了電磁流變液的剪切增稠現象，并討論了這種冪率特性對電磁流變效應及機理的影響。本文在充分考慮了磁流變液的冪率特性的情況下，提出了新的擠壓模型

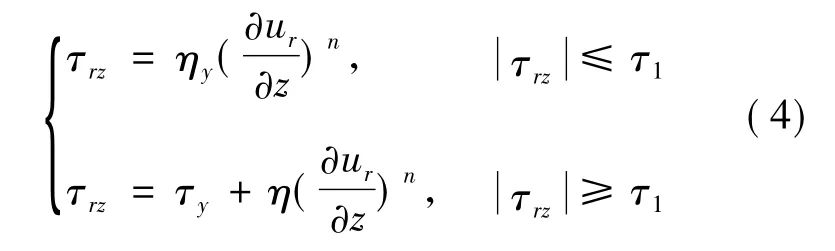
式中:τrz為剪切應力;n為冪率指數;τ1為屈服應力;τy為隨磁場強度而變化的動態屈服應力為剪切應變率;η為磁流變液屈服時的黏度;ηy為磁流變液未屈服時的黏度，ηy比η約大102個數量級。

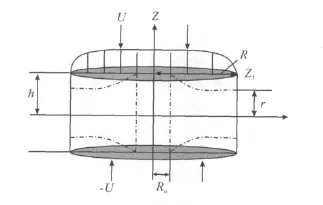
圖1 磁流變液圓盤擠壓流動模型

1.2 邊界滑移條件

潤滑理論引用了臨界剪切應力來描述粘塑性流體的本構關系，并表明了當剪應力達到臨界剪切應力時，其不再隨剪應變率的變化而增加，且流體開始發生滑移［10］。磁流變液作為一種黏度可控的粘塑性流體，其邊界滑移模型可表示為

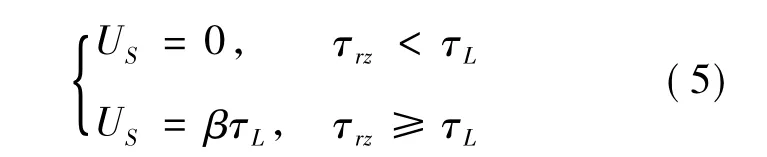
式中:US為滑移速度;τL為臨界剪切應力。

2 擠壓流動分析

在柱坐標系(r，θ，z)，流場速度只有 Ur和 Uz兩個分量［11］。由于磁場的不均勻性，流場屈服面與2個擠壓面并不平行，而是與圓盤相交于r=Ro處。在求解過程中，可把流場分為2個區域［12］。如圖1所示，陰影部分是2圓盤面，虛線為屈服面。在r＜Ro的區域，可把流場看作單一的以高黏度η(H)流動的牛頓流體，稱之為牛頓區;在r＞Ro的區域，圖中虛線包圍的部分為雙黏區，存在屈服面將流場分為屈服區和未屈服區。

2.1 徑向速度和壓力梯度的分布

在r＜Ro的區域，磁流變液可看作黏度很大的牛頓流體，利用流場的對稱性，結合連續方程和擠壓模型式(4)，在邊界滑移條件下進行求解，可得到流場的徑向速度

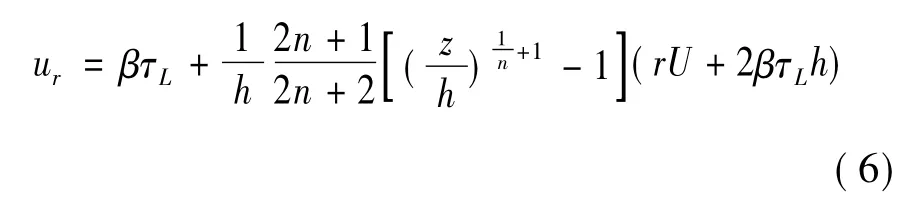
壓力梯度為

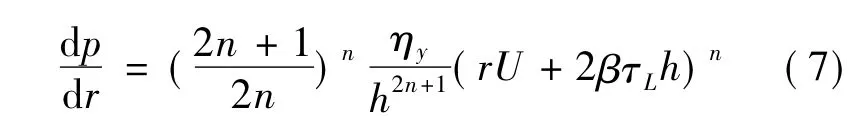
剪切應力為

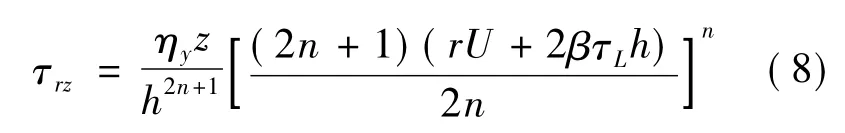
而在r=R0且Z=h時，磁流變液被屈服，此處τrz=τ1，據此可得屈服面與圓盤相交處

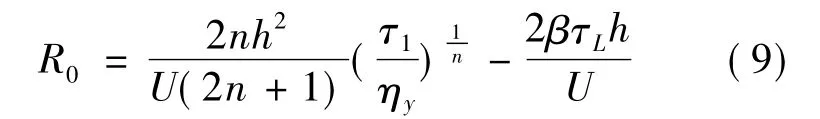
在r＞Ro的區域，由于流場的對稱性，對式(3)積分得到 τrz=(dp/dr)z，而在屈服面上 τrz=τ1，則可知屈服面位置為

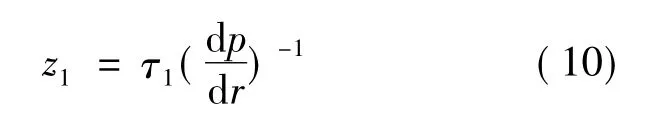
在0≤z≤z1的區域，磁流變液黏度較大，為未屈服區;而z1≤z≤h的區域為屈服區。利用流場的對稱性，結合擠壓模型，在邊界滑移條件下計算得到流場在r＞Ro的徑向速度分布:

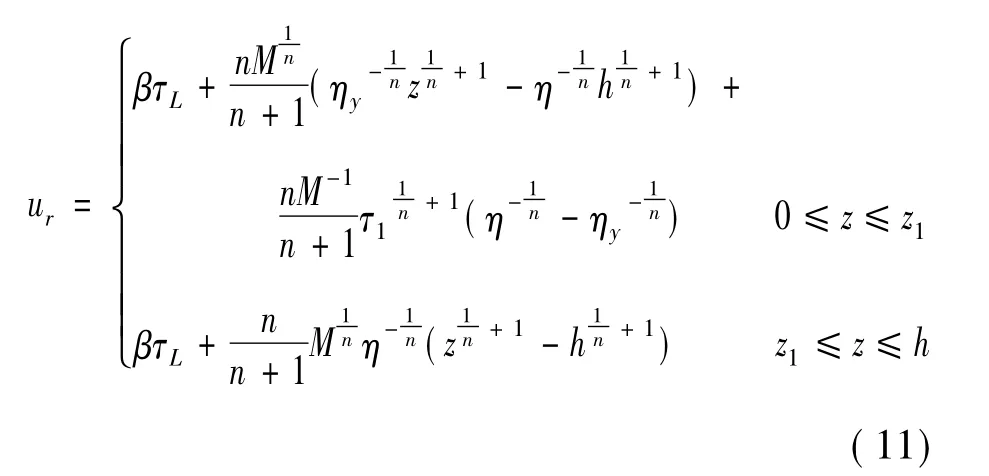
由于流場速度在屈服面位置的連續性，將式(10)帶入式(11)可得壓力梯度的隱式表達式

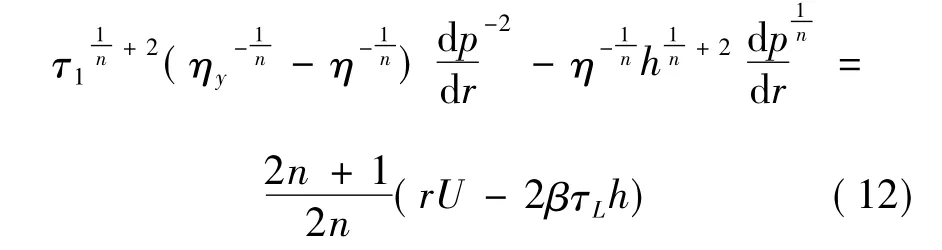
由于實際流場中，壓力梯度是隨r的變大而遞增的［7］，且在r＞Ro的區域，壓力梯度是大于1的，所以式(12)中(dp/dr)－2是小量，可以忽略不計，故壓力梯度可近似表達為

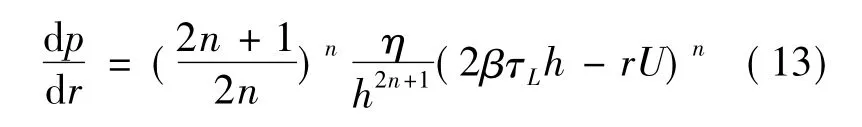
2.2 擠壓力

根據以上計算結果，可知流場壓力梯度的分布為

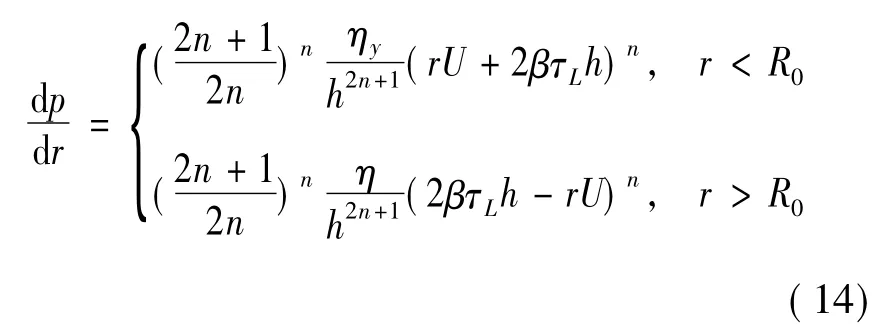
由于擠壓力與壓力梯度存在如下關系

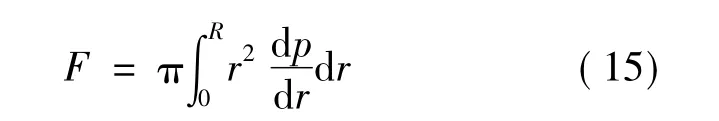
將壓力梯度式代入上式可得圓盤擠壓力的表達:

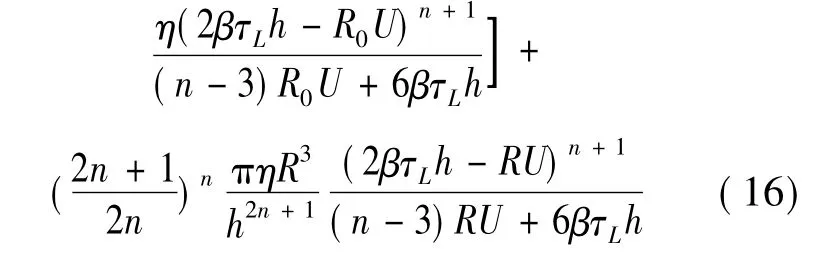
3 結果討論

圓盤擠壓模型的參數取值:h=3 mm，R=40 mm，U=20 mm/s。選用磁流變液材料 MRF-132AD進行分析，其黏度η=0.06 Pa·s。本文不分析磁場強度的變化對流場的影響，故選取特定磁場下的情況進行分析。取磁場強度為H=200 kApm/m，此時 ηy=6 Pa·s，屈服應力 τ1=42 kPa。

3.1 速度場的分布特點

假設流體的滑移速度為US=βτL=2 mm/s，則屈服面與圓盤的徑向交界R0=1.5 mm。在r小于1.5 N的區域，磁流變液接近于牛頓流體，取n=1進行分析。由于流場的對稱性，本文只分析上半個流場，即z大于0的流場。圖2所示為牛頓區的徑向速度分布，由圖可以看出:隨著r的增大，徑向速度增大，但由于流體的高黏性，流動非常緩慢，而且越靠近圓盤處流動越受阻，在z=2.5附近流動幾乎停滯。但邊界附近又開始有流動，這是由于邊界處的滑移使得流體的潤滑性增強。

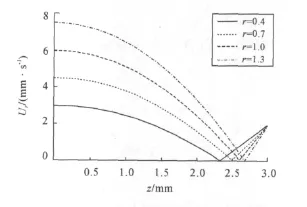
圖2 磁流變液在r＜1.5區域的徑向速度分布

圖3(a)和圖3(b)顯示了磁流變液在雙黏度區徑向速度分布的明顯差異性。可以看出，屈服區的速度值明顯大于未屈服區。未屈服區的速度分布比較平緩，近似于牛頓區;屈服區的速度在z方向近似于遞減的線性關系，越靠近邊界，速度越小。

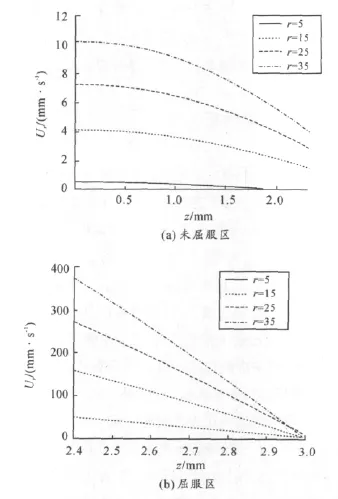
圖3 磁流變液在r＞1.5區域的徑向速度分布

3.2 擠壓力的分析

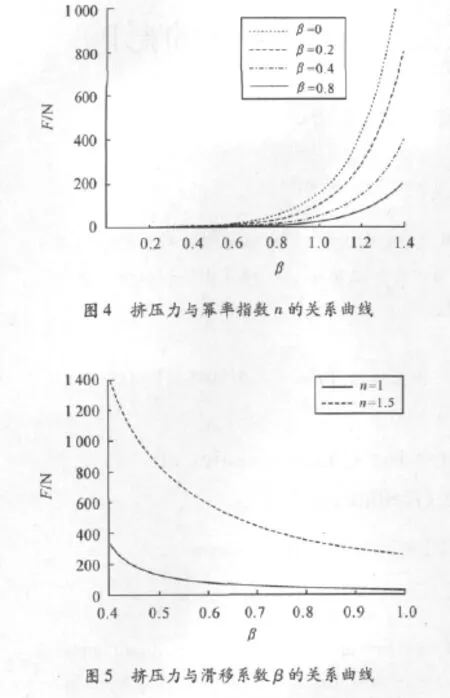
在圓盤擠壓流的實際應用中，圓盤在不同的運動狀態下擠壓力的大小以及它與某些重要參數的關系都有著重要的意義。假設臨界剪切應力為一定值，即取τL=10 kPa進行分析。圖4和圖5分別分析了冪率指數n和滑移系數β對擠壓力的影響。

從圖4可以看出，當n一定時，擠壓力隨著滑移系數的增大而變小。而當n增大時，擠壓力不斷增大。但當n小于1時，擠壓力增大的幅度很小，擠壓力受到的影響幾乎可以忽略。當n大于1時，擠壓力明顯增大，且隨n的增大而不斷遞增。這也驗證了田煜等［5］發現的磁流變液的剪切增稠現象。由于n小于1時，其對擠壓力的影響很小。圖5只取了n=1和n=1.5兩個值進行分析。可以明顯地看出，擠壓力隨著滑移系數的增大而變小。但在n=1時，擠壓力大小的變化很平坦，而n=1.5時，擠壓力的大小變化幅度很大。

4 結束語

在原有的雙黏度模型基礎上，考慮了磁流變液的冪率特性和邊界滑移，建立了新的擠壓模型，將流場分為牛頓區和雙黏區，得到了磁流變液在圓盤間的徑向速度和擠壓力的表達式。通過對圓盤間流場的分析可以看出，屈服區與未屈服區的徑向流動差異很大，邊界滑移對流場的影響也不可忽視。而冪率指數大于1后，其對擠壓力的影響比較明顯，即磁流變液的剪切增稠現象較明顯。為了完善磁流變液的擠壓理論，還應在磁場強度和臨界剪切應力對速度分布和擠壓力的影響上進行深入討論和實驗對比。

［1］Huang J，Zhang J Q，Yang Y，et al.Analysis and design of a cylindrical magneto-rheological fluid brake［J］.JournalofMaterials Processing Technology，2002(129):559－562.

［2］賀建民，黃金，鐘銀輝.磁流變液在圓筒間的粘塑性流動［J］.功能材料，2006，37(6):992 －993.

［3］He J M，Huang J，Fu L J.Design Analysis of Magnetorheological Dampers［J］.Proc SPIE，The International Society for Optical Engineering，2006，6040:475 －480.

［4］Jin Huang，Song Chen，Ping Wang.Analysis and Design of a Cylindrical MR Valve［J］.Advanced Materials Research，2011，197 －198:265 －268.

［5］Alireza Farjoud，Ryan Cavey，Mehdi Ahmadian，et al.Magneto-rheological fluid behavior in squeeze mode［J］.Journial of Smart Materials And Structures，2009，18:1－7.

［6］Laun H M，Rady M，Hassager O.Analytical Solutions for Squeeze Flow with Partial Wall Ship［J］.Journal of Non2 Newtonian Fluid Mechanics，1999，81(1/2):1－15.

［7］徐春暉，黃文彬，徐泳.平行剛性圓盤間有壁面滑移賓漢流體的擠壓流動［J］.中國農業大學學報，2003，8(2):7－10.

［8］廖昌榮，駱靜，李銳，等.基于圓盤擠壓模式的磁流變液阻尼器特性分析［J］.中國公路學報，2010，23(4):107－112.

［9］田煜，蔣繼樂，孟永剛，等.電/磁流變液中的剪切增稠現象［C］//第七屆全國液體和軟物質物理學術會議摘要.西安:西北工業大學出版社，2010.

［10］溫詩鑄，黃平.摩擦學原理［M］.3版.北京:清華大學出版社，2008.

［11］麻建坐，賀建民，黃金.圓筒式磁流變離合器傳動特性分析［J］.重慶理工大學學報:自然科學版，2009，23(3):24－28.

［12］楊士普，任玲，朱克勤.平行圓盤間電流變液的擠壓流研究［J］.功能材料，2006，37(5):690 －696.