基于激勵效用的理想解法

王金山，文 秘

(陸軍軍官學(xué)院，合肥 230031)

理想解法［1］是一種基于理想點的決策方法，其基本思路是定義決策問題的最優(yōu)向量和最劣向量，計算各評價單元與最優(yōu)向量和最劣向量的距離及相對貼近度，并以相對貼近度的大小進行決策。但理想解法存在“理想點”不理想，標準化不成比例，刻意避開主觀偏好的缺點。針對這些缺點，本文提出了基于激勵效用的理想解法，利用激勵效用化方法對決策矩陣進行處理，科學(xué)合理地描述了決策者的主觀偏好，提高了可信度，能更好地解決多指標決策問題。

1 激勵效用

1.1 激勵

按照美國心理學(xué)家費斯延格的公平理論［2］，對組織中員工的有效激勵源于員工個體對組織公平性的認識水平，即員工個體通過“橫向”、“縱向”2種形式的比較，來判斷其所得報酬的公平程度。同樣，決策者在2種方案中間作出選擇時通常面臨如下的激勵判斷:

1)QAIA=QBIB，表示2種方案是一致的，沒有激勵產(chǎn)生的偏好。

2)QAIA＞QBIB，A方案的相對收益要比付出多，產(chǎn)生了正向的激勵，決策者偏好于A方案。

QA為自己對A方案所獲報酬的感覺;IA為自己對A方案投入量的感覺。

“人們對激勵做出反應(yīng)，其余內(nèi)容都是對此的解釋”［3］，決策者的偏好是由于某種激勵產(chǎn)生的。激勵值的大小是一個很好的描述效用值的指標。

1.2 激勵指標的建立

激勵的大小除與收益、付出的相對大小有關(guān)外，還與他們的差值有關(guān)，因此令:

其中:p為激勵指標，刻畫激勵的大小;Q為對方案所獲報酬的感覺;I為對方案合理投入量的感覺。當(dāng)p＜0為負向激勵，p＞0為正向激勵，p=0沒有激勵，p越大激勵程度越高。如果在方案確定之前不知道合理的投入量，可以用各個方案的投入量的平均值代表合理的投入量，即

1.3 激勵的效用

設(shè)效用函數(shù)為U(x)，由于激勵的方向不一致，因此采用歸一化的“S”型效用函數(shù):

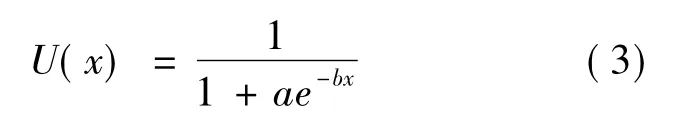
其中a、b為風(fēng)險系數(shù)。可以定義，當(dāng)激勵為1時，效用值為 0.9;激勵為 0時，效用為 0.5。即U(1)=0.9，U(0)=0.5。代入式(3)，可以求出:a=1，b=2.2。那么效用值就代表了決策者對于激勵為p時的偏好程度。可以看出在效用值0.5附近，不論正向激勵還是負向激勵的微小改變都將對效用值產(chǎn)生較大的影響，這符合人們風(fēng)險厭惡的心理。

2 激勵效用理想解法

2.1 決策矩陣

設(shè)有m個方案n個決策屬性指標構(gòu)成的矩陣X=(xij)m×n稱為決策矩陣。應(yīng)該注意，決策屬性指標根據(jù)指標變化方向，大致分為3類:效益型(正向)指標、成本型(逆向)和中間型指標。效益型(正向)指標具有越大越優(yōu)的性質(zhì)，成本型(逆向)指標具有越小越優(yōu)的性質(zhì)，中間型指標具有越靠近理想值越優(yōu)的性質(zhì)。

2.2 決策矩陣的激勵化

在決策矩陣X=(xij)m×n中，根據(jù)決策屬性指標的類型，利用式(2)計算相應(yīng)的激勵指標:

1)對于正向指標fj，取則:pij=

2)對于逆向指標fj，取則:pij=

3)對于中間型指標fj，取ˉx=理想值，則:

矩陣 P=(pij)m×n稱為激勵化矩陣，變換后pij∈(－∞，+∞)，正向指標、逆向指標及中間型指標均被轉(zhuǎn)化為正向指標。

2.3 激勵效用矩陣

將激勵化矩陣 P=(pij)m×n代入式(3)，進行效用化。

得到效用化矩陣 Y=(yij)m×n，滿足 0≤yij≤1，且是正向指標，最優(yōu)值是1，最劣值是0。

2.4 各指標權(quán)重的確定

確定屬性權(quán)重的方法［4］可分為主觀賦權(quán)法、客觀賦權(quán)法兩大類。主觀賦權(quán)法如專家調(diào)查法、標定系數(shù)法、AHP法等，是根據(jù)決策者主觀偏好信息間接或決策者根據(jù)經(jīng)驗直接給出屬性權(quán)重。客觀賦權(quán)法如熵權(quán)法、主成分分析法、多目標優(yōu)化方法等，是根據(jù)決策矩陣信息，通過一定的數(shù)學(xué)模型計算出。記得出的權(quán)重為:

其中ωj表示第j個指標的權(quán)重。由此可以得到加權(quán)激勵效用矩陣

2.5 系統(tǒng)的理想解

很顯然，理想及逆理想效用為

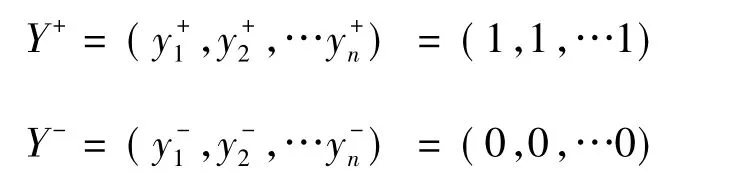
其中:yj+為第j個指標的理想效用;yj－為第j個指標的最不理想效用。所以加權(quán)激勵效用矩陣的理想及逆理想方案分別為

2.6 各方案到理想及逆理想方案的距離

設(shè)系統(tǒng)i到理想系統(tǒng)Z+和到逆理想系統(tǒng)Z－的距離為Di+、Di－，則:

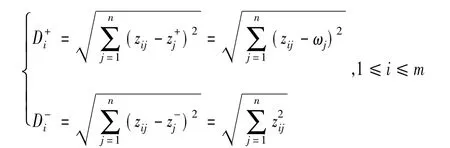
2.7 相對貼近度并排序

3 實例分析

假設(shè)某系統(tǒng)的配置有7種配置方案［5］，如表1所示，利用基于激勵效用的理想解法對7種配置方案的系統(tǒng)效能、費用、生命力、適應(yīng)性、兼容性等指標進行綜合比較，得出最優(yōu)的配置方案。

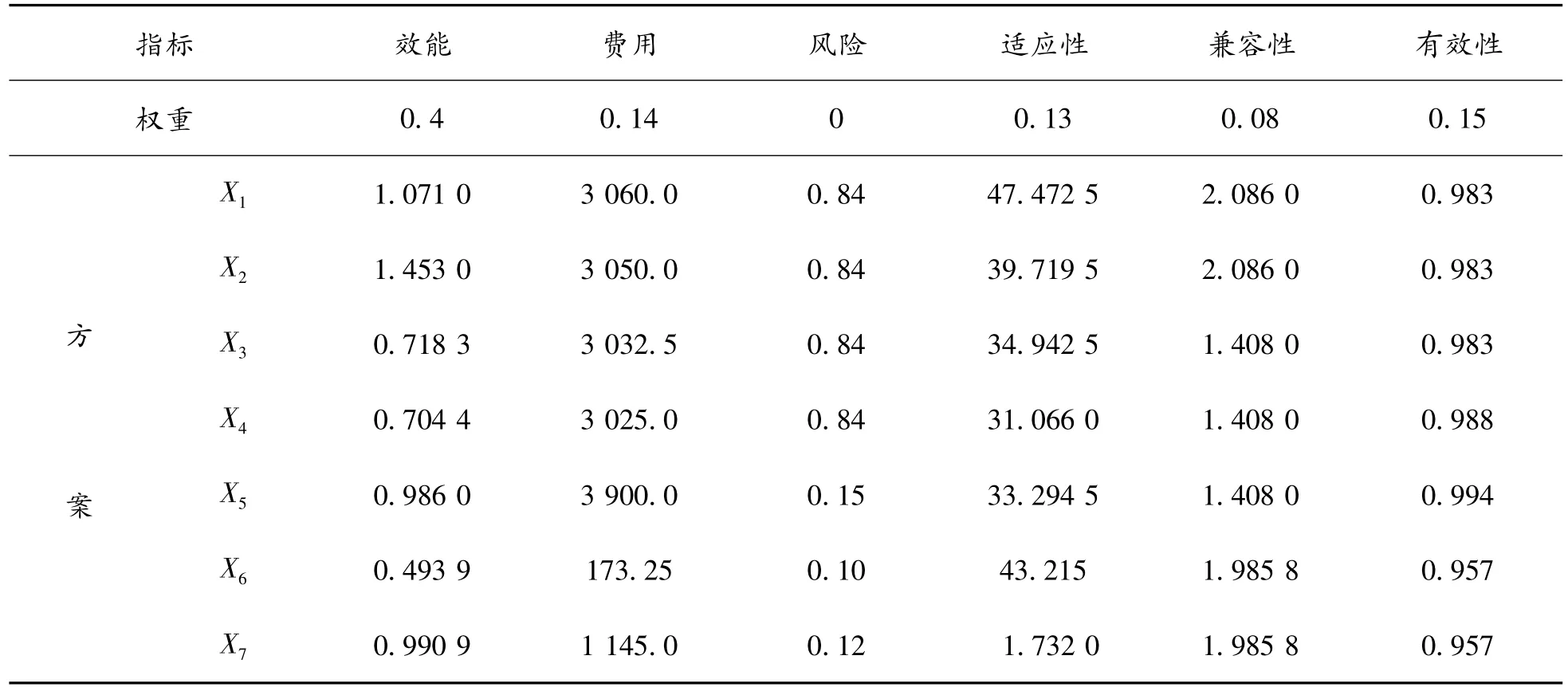
表1 各配置費方案的指標值及各指標值的權(quán)重

在決策指標中，f1、f4、f5、f6是正向指標，f2、f3是逆向指標。由AHP法得到各指標權(quán)重:W=(0.4 0.14 0.1 0.13 0.08 0.15)T。利用激勵化準則及式(4)得到激勵化效用矩陣:

計算各方案的相對貼近度:U+=(0.549 0.654 0.393 0.384 0.510 0.41 0.568)，各個方案的排序結(jié)果為:X2＞X7＞X1＞X5＞X6＞X3＞X4。由排序結(jié)果知，決策者應(yīng)該采用方案X2進行炮兵系統(tǒng)的配置，與參考文獻［5］中的結(jié)果一致。然而，對加權(quán)效用矩陣Z=(zij)m×n各行求和，按總效用的大小進行決策，結(jié)果為X7。可以看出，基于激勵效用的理想解法不僅對傳統(tǒng)的理想解法進行了改進，而且克服了多品質(zhì)因素間的干擾，比直接加權(quán)求總效用的決策準則更加優(yōu)秀。

4 結(jié)束語

建立了基于激勵效用的理想解法，科學(xué)描述了主觀偏好，克服了理想解法“理想點”不理想，標準化不成比例，刻意避開主觀偏好的缺點，擴大了實用性。通過某系統(tǒng)配置方案選取的案例，可以看出該算法能更好地解決多指標決策問題。

［1］崔振才，程興奇，杜守建，等.應(yīng)用逼近理想解法綜合評價水環(huán)境質(zhì)量［J］.水資源保護，2006，22(4):50－52.

［2］李愛媚.基于決策效用的公務(wù)員激勵模型及其應(yīng)用［D］.武漢:華中科技大學(xué)，2007:14－15.

［3］［美］曼昆.經(jīng)濟學(xué)原理:微觀經(jīng)濟學(xué)分冊［M］.4版.梁小民，譯.北京:北京大學(xué)出版社，2006.

［4］袁世龍，王金山.基于熵權(quán)理論理想解法的炮兵C4ISR系統(tǒng)效能評估［J］.火力與控制，2008，33(12):18－83.

［5］周林，王君等.軍事裝備管理預(yù)測與決策［M］.北京:國防工業(yè)出版社，2007:40－41.

［6］慧劍，聶成，安芹力.一種基于改進理想解法的威脅估計方法［J］.彈箭與制導(dǎo)學(xué)報，2003(2):200－201.

［7］顏麗華.效用理論下的再保險研究［D］.秦皇島:燕山大學(xué)，2009:17－18.

［8］JENSON MICAEL，MURPHY KEVIN J.Performance pay and top management incentives［J］.Journal of Political Economy，1990，98(2):255 －264.

［9］Arrow K J.Social choice and individual Values［M］.2ndEd.NEW York:whey，1963.