基于信息熵擴散技術的建筑材料價格水平確定

□文/朱亮亮

引言

發展綠色建筑、開展建筑節能、建設一個環境友好型社會是實現我國可持續發展的必然之路，綠色建筑評價則是實現節能、節耗的必要保障。在綠色建筑評價體系中，一個非常重要的問題是關于建筑材料價格水平測定及統計數據處理。但是，應用傳統建筑材料價格水平測定方法，經常會遇到信息量不足的情況，即所謂的小樣本問題。當用小樣本對母體進行估計時，會產生較大誤差，使得統計分析結果不能體現真實情況。信息擴散技術可以較好地解決這一難題。

一、傳統建筑材料價格水平測定統計數據分析方法

傳統建筑材料價格水平測定及統計數據處理方法為：

1、計算統計數據中材料價格算術平均值：t1；

2、計算統計數據中材料運距算術平均值：t2；

3、計算材料運輸費：t3=t2×運輸費率＋裝卸費＋調車費；

4、計算損耗費：t4=（t1＋t3）×損耗率；

5、計算運輸總費用：t5=t3+t4；

6、計算材料價格：t6=（t1+t5）×（1+保管費率）。

例：某市某種建筑材料有甲、乙、丙三個供貨地點，甲地點出場價格為40元/t，甲距市中心28km；乙地點出場價格為45元/t，乙距市中心30km；丙地點出場價格為38元/t，甲距市中心35km；該材料途中損耗率為5%。該市汽車運輸費0.5元/t.km，裝卸費 3元/t，調車費 1元/t，采購保管費率為2.5%，計算該市該種材料的價格水平。

根據上述傳統建筑材料價格水平統計分析方法，最終可得該市該種材料的平均價格為65.11元。顯然，這里是用容量相對較小的統計數據樣本均值代替母體均值，誤差較大，使得統計分析結果不能體現真實情況。

針對傳統建筑材料價格數據統計分析方法所存在的缺陷，采用信息擴散技術可以實現樣本容量的拓展，較好地解決樣本容量不足的弊端，從而能精確測定出實際價格水平。

應用信息擴散技術的關鍵是合理地確定擴散函數和擴散系數，熵理論為擴散函數和擴散系數的確定提供了理論依據。

二、信息擴散函數的選擇

目前，信息擴散經常使用正態擴散函數和對數正態擴散函數。以一維正態分布信息擴散為例，其擴散函數為：

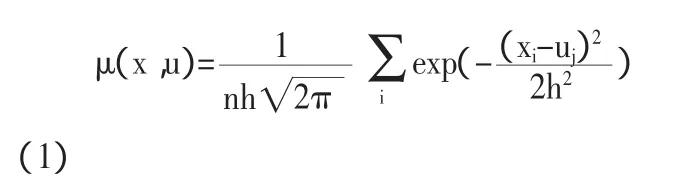
其實，在進行信息擴散時，擴散函數的選擇并不是唯一的，根據部分信息進行信息擴散時，必須選擇具有最大熵的擴散函數，因為在滿足約束條件且熵最大狀態下的概率分布是最不確定、最可能、最隨機，也是最客觀的分布，這就是極大熵原則。

通過應用極大熵原理對各個擴散函數的優劣性進行比較分析得出：正態分布信息擴散函數出現的概率大于其他信息擴散函數。

三、信息擴散系數的確定

對同一擴散函數而言，當采用不同信息擴散系數時，其擴散結果也不同。常規信息擴散系數的確定方法簡單，應用方便，但其需要根據經驗確定，計算結果精度方面有一定的局限性。

應用極大熵原則，提出確定信息擴散系數的新方法，經證明，可得擴散系數：

四、案例分析

以上例為例，應用信息熵擴散技術測定建筑材料價格方法步驟如下：

1、信息擴散步長的確定。取任意兩個樣本值之差的絕對值中的最小值為步長：

2、信息監控點的確定。給定監控初始點u1，步長△，以及監控點個數為m，即：u1＝32，△＝2，m＝10

則擴散監控點為：

uj＝｛32，34，36，38，40，42，44，46，48，50｝

其中，uj是信息擴散的第j個監控點。

3、擴散系數的確定。根據（2）式可得擴散系數：

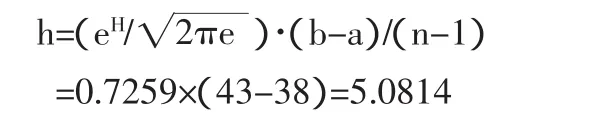
根據（1）式，則一維正態熵擴散估計為：

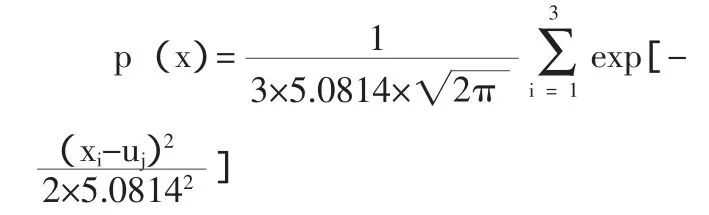
4、計算擴散樣本算術平均值。利用一維正態熵擴散估計最終計算可得擴散材料價格樣本算術平均值：t1；即：t1＝40.93（元）（由于篇幅有限，其計算過程在此省略）；同理，可得擴散材料運距樣本算術平均值：t2；即：t2＝30.2（km）。

5、計算材料平均價格

運輸費：t3=30.2×0.5＋3＋1＝19.1（元/t）

運輸損耗：t4=（40.93＋19.1）×5%＝3（元/t）

運輸總費用：t5=19.1＋3＝22.1（元/t）

材料價格 ：t6=（40.93 ＋22.1）×（1+0.025）＝64.61（元/t）

對于兩種方法所測定的材料價格水平，本文通過對某地區材料價格全面調查的基礎上發現：應用信息熵擴散技術所測定的材料價格平均值與實際所測定的材料價格平均值偏差較小，其精度高于傳統材料價格水平方法所測定的平均價格。

五、結語

傳統材料價格數據統計分析方法，由于實際條件有限，在樣本統計數據收集上，經常會遇到信息量不足的情況，即所謂的小樣本問題，使得統計分析結果不能準確進行材料價格水平測定。本文通過應用信息熵擴散技術，對樣本數據進行分析和推理，將不完備或不確定的知識按特定的擴散函數來近似刻畫，實現樣本容量的擴大，從而實現定額的精確測定。

[1]黃崇福.自然災害風險評價理論與實踐[M].北京：科學出版社，2004.

[2]朱亮亮.基于信息熵擴散技術的網絡計劃工期研究.合作經濟與科技，2009.

[3]閆文周，朱亮亮.基于熵理論的信息擴散系數確定.西安建筑科技大學學報，2009.