基于AWE的工藝轉向架構架優化設計研究

李鵬程，熊禾根

（武漢科技大學 機械自動化學院，武漢 430081）

0 引言

動車組的出現，大大提高列車的運行速度，促進我國經濟與社會的全面發展。但動車的快捷、安全運行，需要相關配套的工藝設備為動車定期檢修服務。動車組檢修共分為五級，通常一級、二級檢修時動車組整列進入檢修基地進行作業；三級及以上級別檢修時需要機車車體與轉向架分離，此時需要由配套的設備承載機車車體。工藝轉向架可以滿足各型動車的需求，可以在機車車體和轉向架分離后，替換轉向架，牽引承載車體，完成車體在各檢修工位間移動的專用工裝設備，因此對工藝轉向架的設計與分析，有很重要的現實意義和應用前景。

一套工藝轉向架通常由動力工藝轉向架和非動力工藝轉向架組成，兩者配對使用，支撐單節機車車體。動力工藝轉向架主要由構架、橫梁、輪對、減速機與電機、軸箱和彈性支撐部件等組成；非動力工藝轉向架無需電機部件，其余結構與動力工藝轉向架相同。動力工藝轉向架的結構模型如圖1所示。

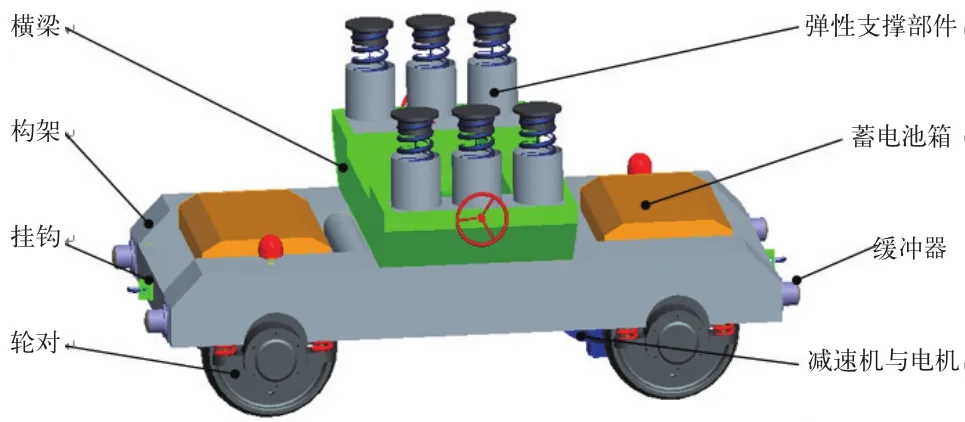
圖1 工藝轉向架結構模型

構架是工藝轉向架的主要承載部件，其空間安裝位置如圖1所示。構架兩側為兩根側梁，每根側梁由內側板、外側板、頂板、彈性支撐板以及筋板焊接而成，其中內、外側板及頂板的厚度均為12mm,筋板厚度為30mm;兩端一根為牽引梁，另一端為端梁，兩者結構完全相同，可實現雙向牽引；中間由兩鋼管橫向連接；另有四根角鋼橫向連接以支撐兩個蓄電池箱。根據現有動車不同車體的要求，參考起重機設計手冊[3]和設計經驗，構架初步設計的總體尺寸：長3800mm,寬2100mm, 高450mm，每根側梁寬425mm，構架模型如圖2所示。

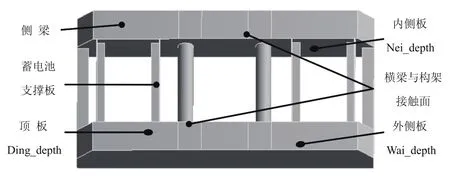
圖2 構架的實體模型

1 構架的有限元模型

為了更好地分析構架在工作中的受力與變形情況，精確的有限元模型是至關重要的。構架的有限元分析是在AWE環境中參數化建模，并對構架模型進行適當的簡化處理，忽略對構架有限元分析影響很小的特征，如安裝在構架上的報警燈、緩沖器、牽引鉤等。該構架采用普通碳鋼Q235材料，其屬性為：屈服極限為235MPa、泊松比為0.3、彈性模量為2×105MPa、密度為7.85×10-9T/mm3。

構架結構復雜，采用切分的方法將構架分割成有規格的結構，采用掃略的方法對其進行有限元網格劃分。網格劃分采用網格形狀比較規則的SOLID186單元（20節點六面體單元），將其離散為27452個節點，3511個單元。構架的AWE有限元模型如圖3所示。

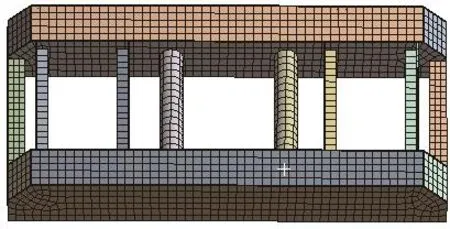
圖3 構架的有限元模型

2 靜力學分析

2.1 邊界條件與載荷的施加

構架主要承受來自機車車體重量的垂直方向載荷，車體重量通過彈性支撐部件作用在橫梁上，再通過橫梁與側梁的四個接觸面作用于側梁上。構架承載的設計要求是50噸，考慮單節機車車體的綜合重量、動載荷等因素，設計按60噸計算與分析。

如前所述，單節機車車體由動力轉向架和非動力轉向架配合支撐，故每臺轉向架構架的垂向載荷為60×9.8/2=294KN，四個接觸面面積為：4×300×425=510000 mm2，計算知施加在四個接觸面上的壓強為0.576 MPa 。靜力學分析時在構架與橫梁的四個接觸面（如圖2所示的橫梁和構架側梁的四個接觸面）處以壓強形式施加載荷，并在構架兩側梁內的四塊彈性支撐板處施加全約束。

2.2 靜力學結果分析

在AWE環境中DS（ANSYS Analysis）模塊對構架進行靜力學分析，構架在壓強載荷作用下，后處理中得到構架的等效應力云圖（如圖4所示）和總變形云圖（如圖5所示）。

由圖4可知構架的等效應力最大值出現在兩側梁的頂板與筋板連接處，最大應力值為85.756MPa。TB/T1335-1996中規定，對焊縫區，最大可能載荷或超常載荷下的許用應力為材料的屈服極限除以1.1倍的安全系數；在運用載荷下許用應力為材料的屈服極限除以1.65倍的安全系數。而本次計算為運營工況，因此Q235鋼板焊接結構材料在運營工況下的許用應力為142MPa，構架的等效應力遠小于構架的許用應力，故構架結構尺寸尚有較大的優化空間。

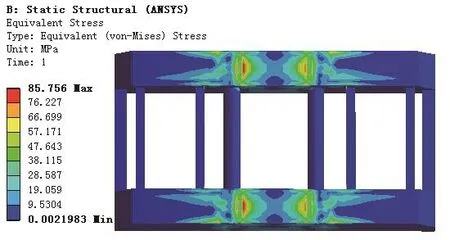
圖4 等效應力云圖

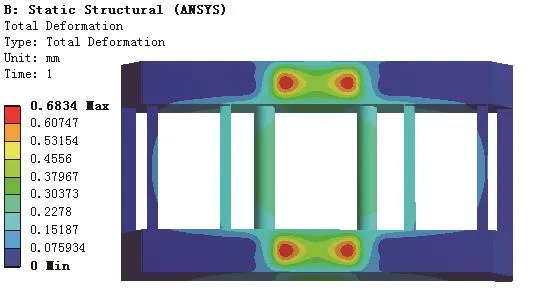
圖5 總變形云圖

由圖5知構架在0.576Mpa壓強下的總變形量最大值為0.6834mm,且出現在構架與橫梁的四個接觸面處。參考《起重機械金屬結構》知構架的許用撓度值為L/700（L代表構架的跨距：2500mm），計算其許用撓度值為3.57mm,故構架的變形量遠小于許用撓度值，其剛度足夠且有很大的冗余空間。

3 構架的優化設計

構架的優化是在靜力學分析的基礎上進行的，由靜力學分析結果知構架有優化的必要。

A W E環境有兩類優化方式：S h a p e Optimization模塊的形狀拓撲優化和Design Explorer（DX）模塊的參數優化。形狀拓撲優化是在線性靜力學和減少實體結構體積的基礎上，尋找需要去除材料的區域的形狀優化方式，此方法比較粗略、簡單、快捷； DX模塊優化是針對結構設計參數的優化。在DX模塊中進行優化設計分析是通過響應面（線）來完成的，其支持的方法是實驗數據法（The Design of Experiments Method）,簡稱DOE法。一旦運算結束，響應面（線）的曲面（線）的擬合就是通過設計點（Design point）來完成的。

構架的優化是采用D X模塊的目標驅動GDO(Goal Driven Optimization)方法的參數優化。GDO法實際是一種多目標優化技術，是從給出的一組樣本（即一定量的設計點）中得到“最佳”的設計點。GDO法根據設計參數的數量，采用DOE實驗設計方法，得到多組設計點。DOE法采用蒙特卡羅抽樣技術，采集樣點并計算每個樣點的響應結果，采用二次插值函數構造設計空間的響應面或設計曲線。構架在AWE環境中采用GDO法優化后可得到三組“較佳”的優化結果，而優化結果主要取決于目標函數，目標函數包括了響應面輸入，輸出變量的目標取值和重要性級別。設計人員可根據多個目標重要性級別的不同和其他目標函數約束條件（如應力值），選出一組綜合性能最佳的設計參數做為優化結果。

3.1 定義設計變量與目標函數

構架的建模、靜力學分析與優化設計均在AWE環境中實現，而優化主要是針對構架兩側梁板厚的優化且兩側梁對應位置板厚一致。

設計變量是在DM模塊中定義的，側梁的主要鋼板厚度作為輸入變量：外側板板厚（Wai_depth）、內側板板厚（Nei_depth）、頂板板厚（Ding_depth），如圖2所示。

目標函數變量是在DS模塊中定義的：構架質量（geometry mass）、最大等效應力（equivalent stress maximum）、總變形（total deformation）。

3.2 優化設計

構架的設計要求是希望在滿足材質強度和剛度的情況下，盡可能降低構架的重量。參考《起重機設計手冊》[3]，知構架的側梁板厚應不小于6mm。各設計變量采用連續型變量，且各變量取值范圍設為6mm～12mm。DX模塊根據三個輸入參數及參數范圍，自動生成15組設計點。結合生成的15組設計點，并確定優化結果時需要設置三個目標函數為求解的最小值（minimize）和重要級別，可得到三組較好的優化方案結果[7]（如表1所示）。重要性級別設置如下：geometry mass為較高級別（higer）、equivalent stress maximum和total deformation為默認等級（default）。

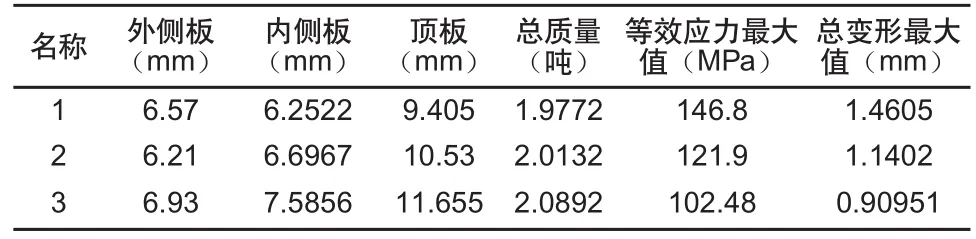
表1 三組較好的優化結果

由表1可知三組優化方案結果中第一組質量最小，第二組等效應力和總變形最小，且三組優化結果的等效應力值均小于142MPa。但優化結果的板厚是小數，需要對其小數部分圓整，便于選材。為保證構架的安全、可靠、輕量化設計等綜合要求，本設計選取頂板板厚為10mm,內側板與外側板板厚均為7mm。

表2 優化前后設計變量與質量參數對比

從表2可知，優化后的參數都有較大的變化，并驗證分析知優化后的方案不僅滿足強度、剛度要求，而且質量比優化前大約減少13.78%，大大減輕構架的重量和降低了生產成本。

4 優化前后構架的模態分析

構架結構重量減輕后，其固有頻率必然降低，因此存在因工作激振頻率引起共振的可能，為此需要驗證優化后構架的振動穩定性。根據構架的工作條件，通常系統發生共振的固有頻率在低階模態處，利用有限元中的模態分析模塊可計算出構架優化前后前6階的固有頻率與振型，結果如表3所示。

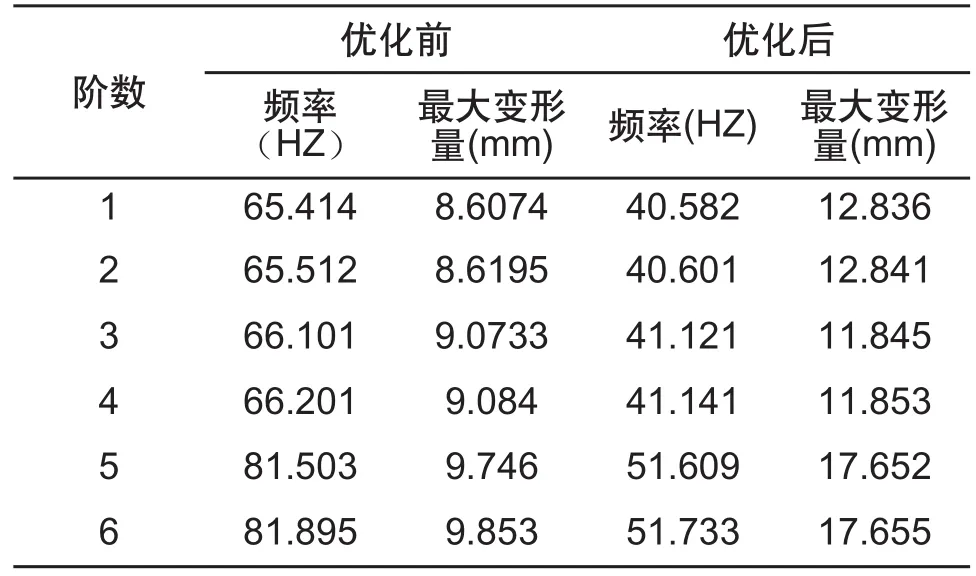
表3 優化前后模態分析結果對比

由表3可知構架在優化后的頻率比優化前小很多，主要是因為構架在減少重量的同時也降低了構架的剛度；另外構架的振型與優化前有較小的變動，且變形主要發生在構架兩側梁的外側板處。電機的額定轉速為1450 r/min，對應頻率為24.167 Hz，小于優化后構架的各階固有頻率，由此可知，優化后的構架可避免共振的發生。

5 結論

根據不同動車車體的要求，初步設計構架尺寸，并在AWE環境下對構架參數化建模、靜力學分析和模態分析，分析可知初步設計的構架尺寸可以滿足強度、剛度與動力學性能；最后對構架進行輕量化設計，在保證強度、剛度的前提下，質量減輕大約13.78%，降低構架的生產成本，同時也避免構架發生共振的現象。輕量化設計沒有大的改變構架的結構，僅對構架兩側梁的板厚進行優化，對構架的研發和生產有重要的參考價值。

[1] 濮良貴,紀名剛.機械設計[M].北京:高等教育出版社,2006.

[2] 周建方.材料力學[M].北京:機械工業出版社,2001.

[3] 張質文等.起重機設計手冊[Z].北京:中國鐵道出版社,1997.

[4] 李兵,何正嘉,陳雪峰.ANSYS Workbench設計、仿真與優化[M].北京:清華法學出版社,2008.

[5] 郄彥灰,王秀紅,劉波,等.基于ANSYS Workbench的中部槽優化研究[J].河北工業大學學報,2010.

[6] 陳俊.基于AWE的滾齒床身結構剛度優化設計[D].南京:南京信息工程大學,2007.

[7] 曾詳亮,李力,肖露.基于ANSYS Workbench的鋼模臺車優化設計[J].工藝與裝備,2009.