在役公路橋梁壽命評估與預測分析

王 旭，管錫琨，黃桂林

(1.黑龍江省交通科學研究所;2.東北林業大學)

在役公路橋梁壽命評估與預測分析

王 旭1，管錫琨2，黃桂林2

(1.黑龍江省交通科學研究所;2.東北林業大學)

大量在役橋梁承載能力不足、老化、破損使得在役橋梁的技術狀況預測和壽命預測成為國內外十分關注的課題。因此，在建立在役橋梁抗力衰減模型及荷載模型的基礎上，引入時變可靠度理論，建立橋梁極限狀態方程。利用Jc法計算橋梁結構時變可靠度指標。引入橋梁工程中的0.85β0這個系數來預測混凝土橋梁的剩余使用壽命。并編制計算混凝土橋梁剩余使用壽命的計算程序，可為同類工程提供參考。

在役橋梁;壽命;預測;可靠度

1 引言

隨著我國經濟的發展，交通運輸事業取得長足的進步，具體表現為交通量猛增，載重量增大。由于設計標準的改變，載重能力的提高，使得許多在役橋梁的承載力變得偏低，橋面偏窄，線型不良。

我國在役混凝土橋梁存在大量的問題。根據有關部門統計，僅公路橋梁就有5 000多座危橋，鐵路橋梁有病害橋6 137座，占橋梁總數的18.8%，其中混凝土橋為2 675座，混凝土裂損722座。隨著混凝土橋梁使用年限的增長，舊橋老化日益嚴重，在我國近20年來，公路交通量和車輛載重不斷增加，公路橋梁負荷日趨加重，這就必然加劇既有橋梁的損傷。而如何預測混凝土橋梁的使用壽命以及采取何種有效的預防措施成為一個迫切需要解決的課題。

混凝土的使用壽命是一個與時間有關的過程。Rostam認為，幾乎所有的混凝土的劣化都經過兩個階段:初始階段和擴展階段。在初始階段，沒有明顯的材料弱化或結構功能退化等現象出現，但保護層被某些侵蝕介質破壞;擴展階段，將出現主動性的損傷并加速發展。Geiker等人將使用壽命定義為三部分時間的和，即t=t1+t2+t3，其中:t1為達到穩定狀態所需要的時間;t2為暴露的混凝土中鋼筋處的氯離子達到臨界濃度所需要的時間;t3為達到必須修補狀態所需時間。

2 預測方法

目前橋梁使用壽命預測的方法有:基于經驗的預測、性能相似對照法的預測、加速試驗法的預測、數學模型法的預測、隨機方法的預測。

2.1 基于經驗的預測

這是一種基于實驗室、現場設定以及經驗知識來預測混凝土服役壽命的方法。這種是在經驗知識的前提下進行直觀推斷。這種方法假定，如果混凝土是遵循標準化生產原則，它必然會有使用壽命期限。此方法擔供了一種假定的混凝土服役壽命預測方法，尤其是當設計年限很短或者混凝土在非嚴酷的環境中工作時，在使用期內混凝土能充分地滿足性能要求。但這個理論使用時有如下一些局限性。

(1)要預測的混凝土服役期大于已有期限內混凝土的經驗知識時。

(2)遇到新的環境或存在侵蝕性的環境時。

(3)應用全新的混凝土材料時。

對混凝土使用壽命進行半定量預測的常用方法是基于試驗或由具有豐富現場經驗的專家判斷。只要按照標準設計與施工，則混凝土應該具有所需要的壽命。這一方法的缺點是:當所需預測的混凝土壽命超過專家經驗、應用于新的環境或使用新型混凝土材料時容易產生失誤。而且研究實例表明，對混凝土耐久性的經驗性或者定性評論僅僅是一種預測，尚不能形成有效預測服役壽命的基礎，認為根據經驗或定性估計不能作為使用壽命預測的可靠基礎。

2.2 性能相似對照法的預測

這種預測方法尚未普遍應用。但其應用會隨著老化混凝土結構的增加而增長。用這種相似對照材料性能的方法假定，如果混凝土在確認時間內是可靠的，則處于相似環境內的類似混凝土也應具有相同的可靠期。此方法存在的問題是任何混凝土結構由于材料、尺寸、施工情況、所處工作環境與施加荷載的不同都具有唯一性;而且多年來混凝土材料的性能也發生了改變。而且不同的微氣候(混凝土表面的環境)會對混凝土耐久性造成不可預測的影響。相對應的是化學和礦物外加劑的發展也促進了高耐久性的高性能混凝土的應用，而且外加劑、摻合料也在變化，所以，即使所處環境是基本一致，相似對照法比較新舊混凝土之間的耐久性也相當困難，且存在著相當大的局限性，所以預測混凝土的壽命仍然不能一擊而中。

2.3 加速實驗法的預測

混凝土的耐久性與滲透性聯系密切，因此國內外學者對混凝土的滲透性能進行了大量研究工作并提出了相應的測試方法，有透水法、透氣法、混凝土氯離子滲透性測試法。

目前，普遍認為混凝土的滲透性能可以由氯離子的傳輸性來體現，而且只要鋼筋周圍的氯離子達到一定的濃度，而且其他條件同時具備就會發生鋼筋銹蝕。此時即可認為結構壽命達到終結。因此，可以將混凝土中氯離子達到臨界濃度的時間看作混凝土結構的使用壽命。

上述橋梁使用壽命預測方法只注重一個老化、劣化過程，然而多個損傷進程會同時發生，或者存在環境與荷載的交互作用，都會導致劣化。在役橋梁因導致劣化的因素難以識別，這種交互作用效應使壽命預測復雜化。制約鋼筋混凝土結構的服役壽命的主要因素包括:氯離子侵蝕、碳化作用、化學物質(酸性物質和硫酸鹽)侵蝕、凍融循環、荷載(疲勞、振動、局部超載)。特殊情況下，只考慮一個主要制約因素的作用并據此進行壽命預測;當多因素作用時，因可用的交互作用影響資料有限，著重關注前述的顯著環境因素的影響。因而應用概率方法進行結構的剩余使用壽命預測是非常合理的方法。

3 隨機方法的預測

影響在役橋梁的使用壽命的各因素都是隨機變量，甚至是隨時間變化的隨機過程，所以，應用隨機方法進行橋梁的剩余使用壽命的預測是非常合理的。

隨機方法是在建立在橋梁抗力衰減模型及荷載模型的基礎上，引入時變可靠度理論，建立橋梁極限狀態方程。利用Jc法計算橋梁結構時變可靠指標。引入橋梁工程中的0.85β0這個系數來預測混凝土梁橋的剩余使用壽命。并編制計算混凝土橋梁剩余使用壽命的計算程序。

(1)建立在役橋梁的抗力模型

首先考慮混凝土碳化、鋼筋銹蝕、鋼筋強度、混凝土強度等因素對橋梁結構的抗力衰減的影響，建立結構的抗力衰減模型。

(2)建立在役橋梁的荷載模型

公路橋梁的荷載模型主要由活載和恒載組成，活載效應取決于車輛荷載、軸重、軸的類型、橋上的車輛數、路面狀況及結構構件的剛度等。這些參數在整個服役過程中都是隨時間變化的隨機變量。對于在役橋梁結構，應盡量使用現場檢測、調查得到的數據來估計及修正荷載效應模型。

(3)進行壽命預測

①建立可靠度極限狀態方程

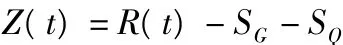
②計算結構的時變可靠度指標

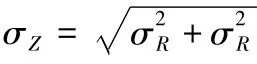
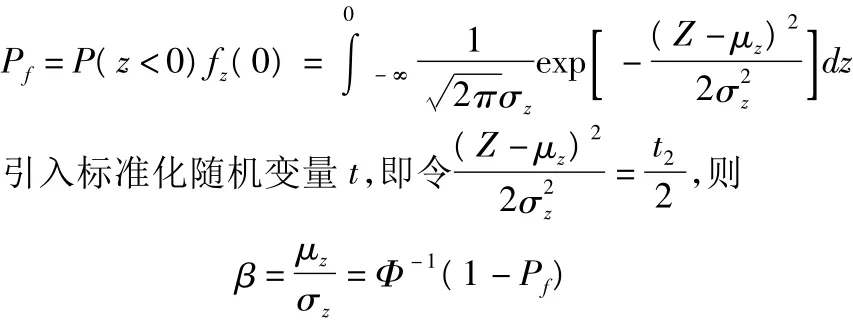
根據結構可靠度的定義，結構服役過程中的動態可靠度可定義為

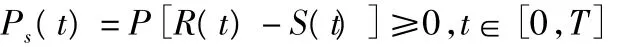
式中:R(t)為結構抗力隨機過程;S(t)為作用效應隨機過程;t為結構使用壽命。

結構動態可靠指標可以表示為

可靠指標是結構服役時間t的函數。

利用Jc法求解可靠度指標迭代計算可知β值的一般式為

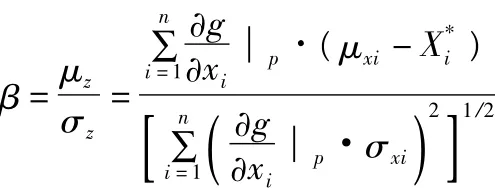
③以0.85β0為準則，編制計算程序，預測在役橋梁在一定可靠度水平下的使用壽命。

4 工程實例

4.1 工程概況

某大橋位于綏北公路海倫至北安段，建于1993年，橋跨布置為10×20 m鋼筋混凝土T形梁橋。設計荷載為汽車－20級;掛車－100。橋面鋪裝為8 cm厚瀝青混凝土。墩臺采用樁柱式橋臺，樁柱式橋墩，鉆孔樁基礎。橋面寬為凈－10 m+2×1 m防撞護欄。

4.2 壽命預測

本橋梁的荷載橫向分布系數采用剛接橫梁法計算，經過計算得出1#梁荷載橫向分布系數為0.507，2#梁荷載橫向分布系數為0.432，3#梁荷載橫向分布系數為0.407。由于進行橋梁剩余使用壽命預測時，將該橋的七片T梁看作是串連系統，若任何一片梁失效將導致整座橋梁失效，因1#梁的荷載恒向分布系數最大，故以1號梁為受力最不利梁來計算橋梁的使用壽命。

首先寫出耐久性極限狀態方程，即

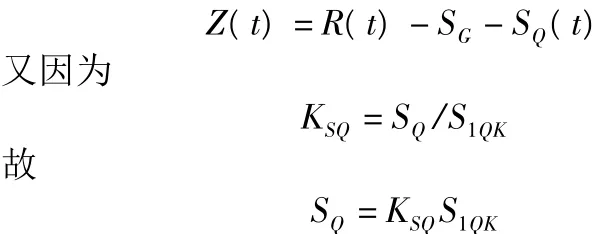
考慮按彎矩失效模式取值，即

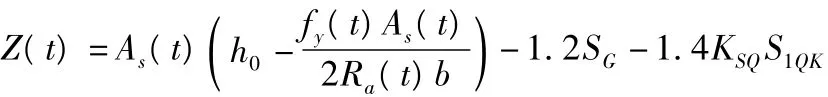
式中各個參數的意義如下

b為受壓區梁寬，為常量;h0為梁的實際有效高度;fy(t)為鋼筋抗拉強度隨時間變化的函數，正態變量;Ra(t)為混凝土抗壓強度隨時間變化的函數，正態變量;As(t)為鋼筋截面面積隨時間變化的函數;SG為恒載效應值;S1QK為標準車輛荷載計算的效應值;KSQ為荷載效應比。

在本案例中，經計算

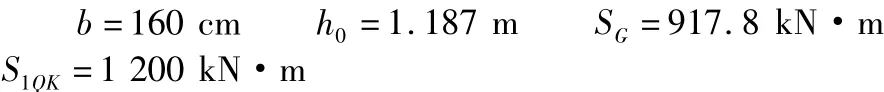
鋼筋截面面積平均值取76 cm2，鋼筋截面面積標準差取3 cm2;鋼筋強度平均值取為360 MPa，鋼筋強度標準差為21.4 MPa;混凝土強度的平均值為14.3 MPa，混凝土強度的標準差為0.78 MPa;其余各值根據前面所列表格的內容取值。然后把這些數據輸入到橋梁剩余使用壽命預測程序中。

取目標可靠指標β0=4.2，對橋梁剩余使用壽命進行預測，首先輸入各參數到程序界面。

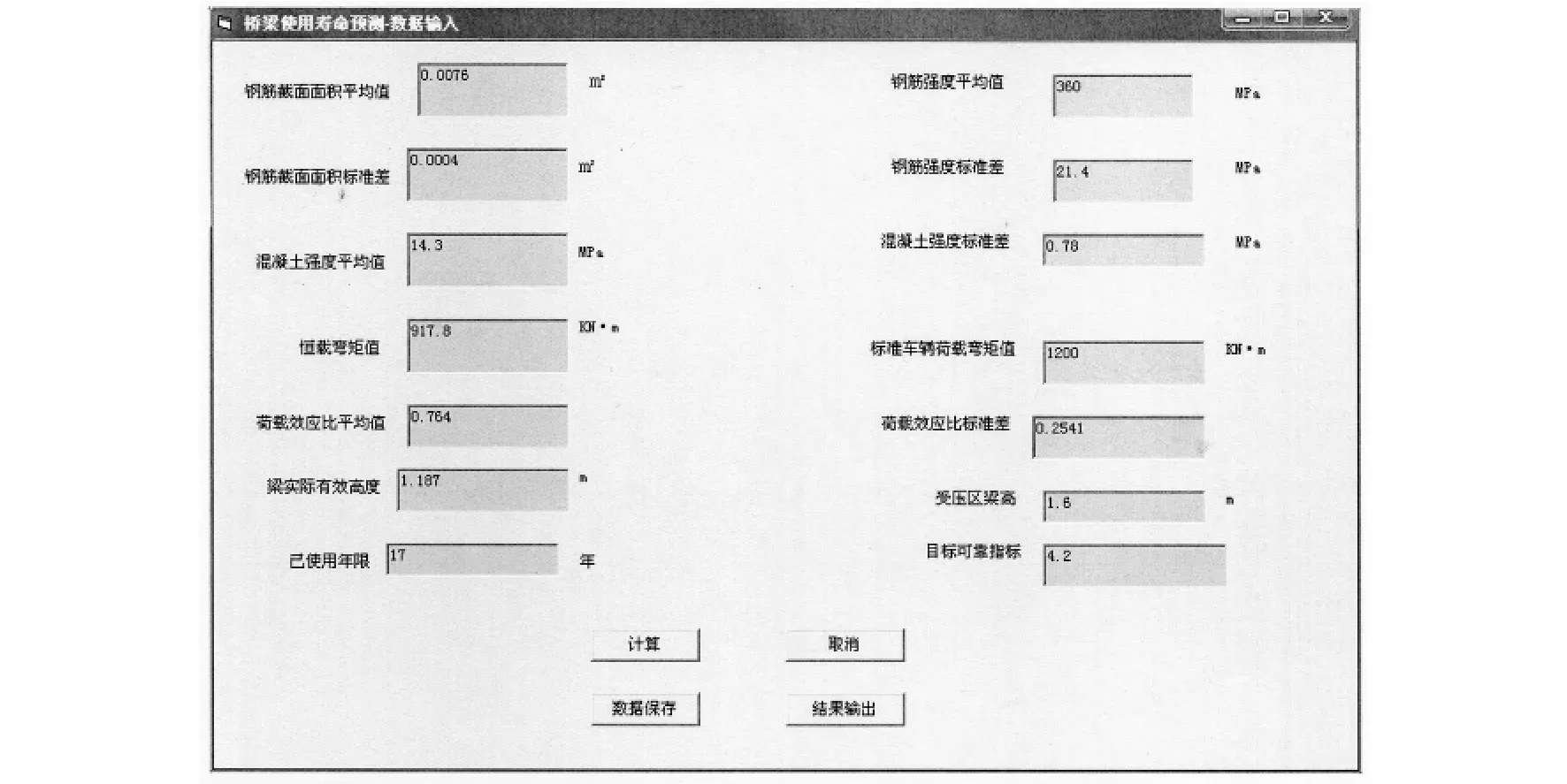
圖1 數據輸入圖

點擊結果輸出，輸出如下結果。

圖2 結果輸入圖

由程序輸出結果可知，該橋梁在已經使用17年后，剩余使用壽命為38年。

5 結論

(1)在役橋梁是社會的寶貴財產，是保證交通安全暢通的關鍵。但大量在役橋梁承載能力不足、老化、破損己成為世界性的問題。在役橋梁技術狀況預測和壽命預測，己成為國內外十分關注的課題。

(2)基于經驗的預測法僅僅是一種預測，尚不能形成有效的預測服役壽命的基礎;相似對照法比較新舊混凝土之間的耐久性相當困難，且存在著相當大的局限性，所以預測混凝土的壽命仍然不能一擊而中;而加速實驗可操作性差、實驗年限過長;而影響在役橋梁的使用壽命的各因素都是隨機變量，甚至是隨時間變化的隨機過程，所以，應用隨機方法進行橋梁的剩余使用壽命的預測是非常合理的。

(3)建立在役橋梁抗力衰減模型及荷載模型的基礎上，引入時變可靠度理論，建立橋梁極限狀態方程。利用Jc法計算橋梁結構時變可靠指標。引入橋梁工程中的0.85β0這個系數來預測混凝土梁橋的剩余使用壽命。并編制計算混凝土橋梁剩余使用壽命的計算程序，可為同類工程提供參考。

［1］王有志等.橋梁的可靠性評估與加固［M］.北京:中國水利水電出版社，2002.

［2］徐海軍.混凝土耐久壽命預測的研究方法綜述［J］.廣州建筑，2006，(1).

［3］Clifton J R .Predicting the service life of concrete 2000.london:E＆FN Spon 1993.

［4］郝曉麗.氯腐蝕環境混凝土耐久性與壽命預測［M］.西安:西安建筑科技大學，2004.

［5］焦鵬飛.在役混凝土橋梁剩余使用壽命預測研究［D］.長安大學碩士學位論文，2004.

U445

C

1008－3383(2011)12－0067－03

2011－10－11