環量控制尾梁參數對直升機尾梁側向推力的影響
董振興,高亞東,王華明
(南京航空航天大學直升機旋翼動力學重點實驗室,江蘇南京 210016)
0 引言
無尾槳概念(NOTAR)是直升機技術的新發展,它改變了傳統的尾槳設計概念,利用環量控制尾梁提供旋翼反扭矩所需的力,從而取消尾槳,從根本上解決尾槳給直升機帶來的各種問題。其結構簡單,安全性好,改善了可靠性和維護性,減少了直升機的振動和噪聲,使乘坐舒適性得到改善。
環量控制由邊界層控制發展而來,指的是后緣為圓弧形的翼型后部上表面開縫,從縫中噴出氣流,挾帶著上面的氣流繞后緣流動,直到后緣附近某點分離,這樣在該翼型上形成環量,產生升力。普通翼型的上表面氣流不可能繞過尖削后緣,而是在后緣分離。環量控制翼型后緣為圓弧形,圓柱[1-2]就是這種翼型的特例。無尾槳直升機,就采用了環量控制技術。這種直升機的機身為圓柱或近似為圓柱,以旋翼的尾流為來流,在機身上引出壁面噴流后,產生一側向力以平衡旋翼的扭矩,從而取代了尾槳,簡化了直升機的設計。
1 計算模型
1.1 建立幾何模型
MD520N是一架技術成熟的無尾槳直升機,它采用的環量控制尾梁縫隙寬度與尾梁直徑之比h∶D=0.009,縫隙長度與旋翼直徑之比為 0.18。參照該機型數據以及文獻[3],建立本文的計算模型。模型的主要參數如表1所示。
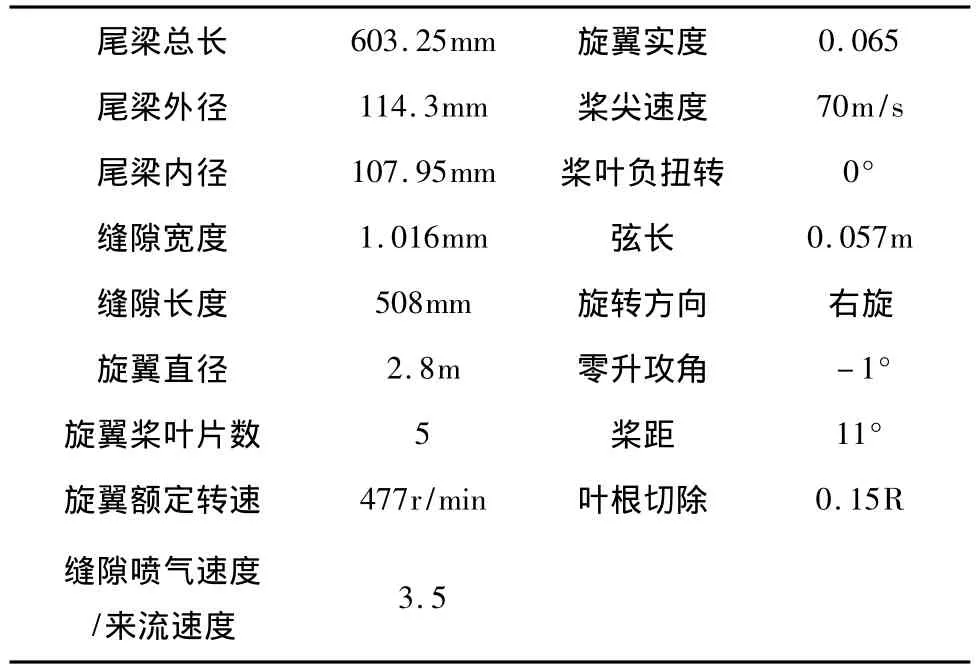
表1 旋翼及尾梁模型主要參數
動量源方法[4]是把槳葉對氣流的作用以動量源的形式來表示,并忽略槳葉附近流場的細節特征,把周期性流動通過時間平均轉化為“準定常”流動。在保證旋翼下洗流流場本質屬性的前提下,上述方法舍去求解旋翼槳葉周圍流場的流動細節給計算精度提出的高要求。同時,由于用圍繞整個槳盤的網格來取代圍繞槳葉的貼體網格,減小了網格生成難度和網格數目,有效節省了計算時間。確定動量源項需要通過配平獲得,根據力平衡關系得到輸入參數并加入到自定義函數中,實現動量源項的模擬。一般計算流程如下:已知旋翼的轉速、來流速度和槳葉幾何參數,使用葉素理論求出槳葉微段在剖面坐標系下的升力、阻力,然后通過坐標變換,把槳葉微段在剖面坐標系下的受力情況轉化為在計算域坐標系下的受力情況,得到槳盤前后的壓力差,即為動量源。本文采用動量源方法模擬旋翼下洗流流場,旋翼槳葉將由槳盤模型(圓盤)代表,即通過槳盤對流場力的作用來模擬旋翼槳葉對流場影響。由于本文主要研究環量控制尾梁的工作原理,以及風洞和旋翼下洗流中動量系數、縫隙幾何參數等對尾梁氣動力的影響,所以工作重點是建立環量控制尾梁分析模型,對機身則進行了適當的簡化處理。除此之外,為減少后期網格劃分工作量,降低網格生成難度,本文對幾何模型作了合理簡化:
1)對尾梁的簡化處理。把真實的尾梁簡化為一個圓柱體,并在適當位置開縫。由于噴氣錐側向噴氣,產生側向力,且處于尾梁尾部對環量控制影響不大,所以未在模型上構建。
2)對旋翼的簡化處理。把真實的五片槳葉簡化為一個等半徑的作用盤,除去中間槳轂部分,在計算時向槳盤的面網格單元載入動量源項。
利用三維設計軟件CATIA建立機體模型,主要采用曲面造型設計和分塊設計兩大模塊來完成,最后封閉成一個實體,再檢查連續性,避免出現開口,生成模型如圖1所示。

圖1 機體三維模型
1.2 建立計算域
為了更好地模擬尾梁氣動特性,本文建立了一個長為10m,半徑為2m的圓柱形計算域。為了減少網格數量,提高計算效率,把圓柱形計算域與機身之間的區域分為4個部分,從外到里分兩層,外層為一個區域,內層從前到后依次為入口段、中間段與出口段。
1.3 劃分網格
為了簡單而準確地滿足邊界條件,首先生成貼體(單域)計算網格,即附面層網格,然后分區域劃分體網格,即根據外形特點將總體流場分成若干子域,對每個子域分別建立網格。本文中機身和尾梁表面(不含縫隙)采用非結構三角形網格,縫隙處采用四邊形結構網格,兩側小三角面采用非結構網格,旋翼用一圓盤來代替,在圓盤上劃分結構化網格,除去中間槳轂部分,體網格從內向外逐塊生成,首先生成縫隙噴口處小體的結構六面體網格,然后生成內層小體的非結構四面體體網格,最后是中間層和外層的結構六面體網格,從而完成整個計算域網格。體網格生成需要花費較多時間,需進行初始化與細化等操作,完成后約為216萬體網格。
2 計算結果及分析
本文采用k-ε湍流模型,由于旋翼下洗流速度不高,考慮氣流粘性影響,計算時控制方程采用了定常、不可壓、有粘的納維爾-斯托克斯方程[5],將動量源程序導入到FLUENT軟件中模擬旋翼下洗流,根據下洗流的速度改變縫隙的噴氣速度,即改變動量系數,得到了尾梁模型上氣動力隨縫隙數目、大小和位置、動量系數等基本參數的變化情況。
2.1 表面壓力分布
圖2給出無環量控制(縫隙不噴氣,Cμ=0)時尾梁壓力分布曲線。曲線1表示通過勢流理論計算的結果。曲線2和3分別為模擬旋翼下洗流和風洞流場中尾梁表面壓力分布。由于尾梁表面分離區壓力基本保持不變,曲線平坦,曲線端點就是分離點。從風洞中尾梁表面壓力分布曲線可知分離點大約在75°附近,而在旋翼下洗流中的壓力分布曲線上,分離點分別在150°和240°附近。從圓柱體邊界層分離理論可知,分離點位置不但與雷諾數有關,還與模型表面粗糙度和來流紊流度有關。實際旋翼下洗流不是垂直下降的,而是螺旋下降的極不穩定的氣流,其紊流度很高,盡管雷諾數較低,但紊流使尾梁表面邊界層在分離前就已經由層流過渡到紊流,使分離點后移,引起負壓增大,因而圖2中曲線2的最高點(駐點)并不在0°,而是在10°左右,這是由于旋翼下洗流并不是垂直下降的,而是呈螺旋形斜向下打到尾梁上,相對尾梁頂部存在大約10°的夾角,使分離點推遲10°,即分離點距前駐點140°。
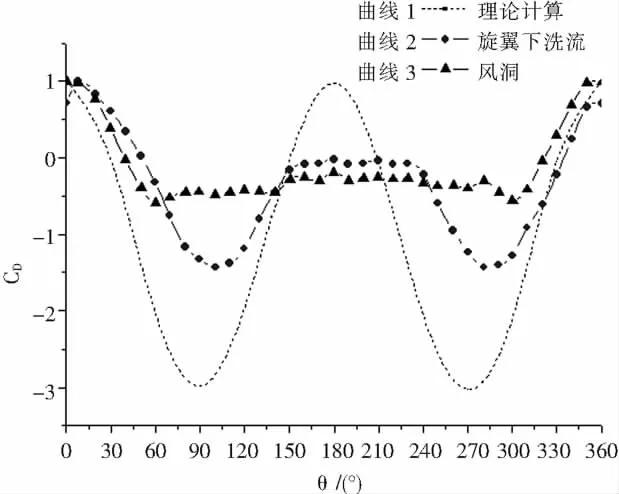
圖2 尾梁表面壓力分布

圖3 有環量控制時尾梁截面附件流場流線圖
圖3為尾梁附近流場流線,從圖中看出當有環量控制時,縫隙噴出氣流給尾梁表面氣流增加能量,使氣流大量流向尾梁未開口的一側,局部負壓大大提高,分離點后移,造成尾梁兩側壓力分布不對稱;處于90°一側的尾梁表面負壓顯著增加,而另一側變化不大,從而在尾梁上產生指向負壓較大一側的側向力。其中,尾梁尾部的環量控制效率低于中部。在尾梁與機身的結合處氣流分離嚴重,對旋翼下洗流干擾嚴重,導致單縫隨方位角變化時,尾梁氣動力變化劇烈,環量控制效率較低。因而,環量控制效率沿尾梁從前到后的順序先逐漸變高后逐漸變低,同時也決定了單縫不適合工程應用。
2.2 動量系數的影響
從圖4中C1隨Cμ的變化曲線可以看出,同前期風洞流場中相似,處于旋翼下洗流內的尾梁的升力(側向力)系數C1隨動量系數Cμ的增大而增大,開始曲線斜率較大,當Cμ>0.4時逐漸變得平緩,綜合考慮阻力系數和升阻比后得出最優動量系數Cμ大約在0.4附近,此時環量控制效率最高。該規律與麥道公司的風洞實驗結果[6]相符。
2.3 縫隙幾何參數的影響
對于旋翼下洗流中縫隙大小和位置對環量控制尾梁氣動力的影響如圖5中所示,縫隙寬度越大,升力系數越小,且與風洞中單縫最佳位置不同,在旋翼下洗流流場中,單縫開在140°方位時升力系數最大,環量控制效果最好,該結論與文獻[7]研究結果相符。
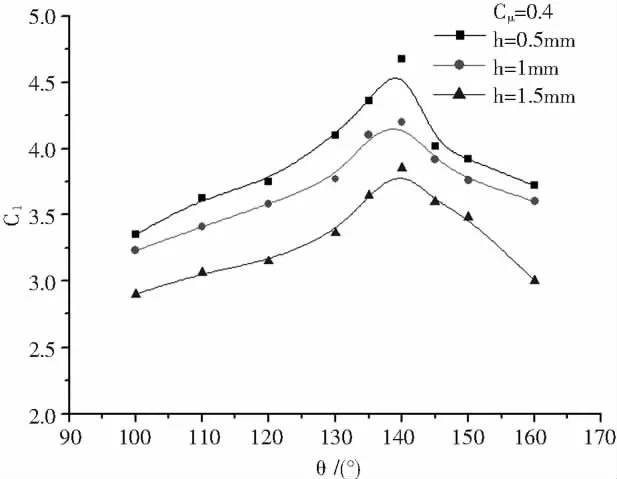
圖5 升力系數隨方位角變化的曲線
前期的研究發現,風洞中最佳雙縫位置之間的夾角是60°,旋翼下洗流中氣流速度與尾梁縱向對稱面的夾角的影響可看作是縫隙位置的影響,可按照這個夾角以及縫隙方位角由小到大的順序,縫隙寬度前小后大的布置方式建立模型。改變縫隙的位置,計算雙縫在不同位置時尾梁氣動力的變化。圖6表示升力系數、阻力系數和升阻比隨雙縫方位角變化規律,其中橫坐標是第一條縫的方位角。當第一條縫位于140°,即雙縫方位角分別為80°和140°時,升力系數Cl最大,此時升阻比Cf也最大。麥道公司無尾槳直升機MD520N的環量控制尾梁雙縫正是這兩個值[3]。由此確定在旋翼下洗流中雙縫最佳方位角為80°和140°。
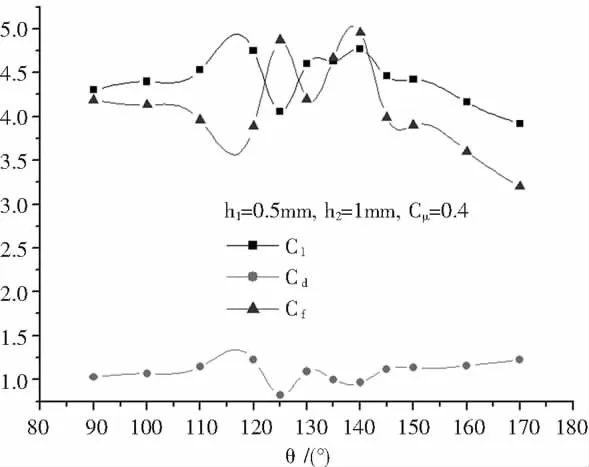
圖6 升、阻力系數和升阻比隨雙縫方位角變化的曲線
3 結論
本文主要研究了處于旋翼下洗流中的環量控制尾梁的氣動特性,以及動量系數、縫隙幾何參數等對尾梁側向氣動力的影響。
1)通過仿真計算,并與以往實驗對比,環量控制尾梁最佳動量系數在0.4附近。
2)對于單縫,最佳方位角為140°;對于雙縫,雙縫的最佳位置為80°和140°。
3)雙縫環量控制效率比單縫高,適用于工程應用。按方位角從小到大的順序,縫隙寬度采用前小后大方式布置時,環量控制效率明顯大于前大后小的布置方式。
[1]Sun M,Pai S I.Aerodynamics force calculations of an elliptical circulation control airfoils[J].J of Aircraft,1996,23(9):679-680.
[2]Ghee T A ,Leishman J G.Unsteady circulation control aerodynamics of a circular cylinder with periodic jet blowing[J].AIAA J,1992,30(2):289-299.
[3]Fisher D T.Wind Tunnel Performance Comparative Test Results of a Circular Cylinder And 50%Ellipse Tailboom for Circulation Control Ant-torque Application[D].Thesis of Naval Postgraduate School.March,1994.7-30
[4]王博.基于CFD方法的直升機旋翼/機身流場模擬及分析[D].南京:南京航空航天大學,2007.20-30.
[5]錢翼稷,編著.空氣動力學[M].北京:北京航空航天大學出版社,2005.2.65-70.
[6]Logan,A H.Evaluation of a Circulation Control Tail Boom for Yaw Control[M].Hughes Helicopters,Inc.,USARTL-TR-79-10,April 1978.10-20.
[7]Chaffin M S,Berry J D.Navier-Stokes simulation of a rotor using a distributed pressure disk method[C].Proceedings of 51st Annual Forum of AHS,1995.25-45.

