鋁泡沫復合材料夾芯梁的彎曲性能

周廣濤，王新筑

(1.華僑大學 機電及自動化學院，廈門 361021;2.重慶大學 a.工程力學系力學博士后流動站，b.煤炭災害動力學與控制國家重點實驗室，重慶 400044)

金屬泡沫材料是20世紀80年代后期國際上迅速發展起來的一種物理功能與結構一體化的新型工程材料，多孔結構和金屬特征使其得以具備其他實芯材料未有的功能，如防震、吸聲、屏蔽、質輕及結構功能一體化等突出特點。其中最有前途的應用是作為輕－硬夾芯結構的芯子，使得金屬泡沫夾芯結構在具有低密度的同時兼有良好的抗剪切和斷裂強度。金屬泡沫夾芯結構比目前廣泛使用的蜂窩夾芯結構具有一系列突出特點，如在溫度超過300°時力學性能仍能保持穩定，抗腐蝕性強，能加工成復雜形狀等［1－2］，一度成為研究的重點。彎曲載荷是夾芯結構在工程應用中受到的主要載荷形式，因此在力學性能的研究上，彎曲載荷是該材料研究的主要領域。何德坪等［3－5］根據球形孔鋁泡沫合金和鋁泡沫夾芯梁的三點彎曲載荷－位移曲線，研究了4種常見破壞模式，并建立了破壞模式圖。虞吉林等［6］利用霍普金森裝置研究了開孔金屬泡沫芯子鋁面板夾芯結構在靜載和動載彎曲作用下的失效機制。Gibson等［7－9］研究了三點彎曲載荷作用下的金屬面板鋁泡沫夾芯結構分別在常溫和高溫下的失效模式和蠕變行為，得到了失效載荷圖。Fleck等［10］從理論和試驗上研究了不同邊界條件下的鋁面板鋁合金泡沫芯子夾芯結構在三點彎曲載荷作用下的失效機制，并繪制了失效機制圖。還有其他一些學者對完好和面板含缺陷的金屬面板金屬泡沫夾芯結構在四點彎曲載荷下的破壞模式、失效機制及承載能力進行了研究［11－15］。

目前，國內外學者研究的金屬泡沫夾芯結構其面板多為金屬面板，金屬泡沫復合材料面板要比金屬泡沫金屬面板夾芯結構具有更明顯的優勢。因此，本文自行設計和制造了金屬泡沫復合材料夾芯結構，并對該結構的彎曲力學性能進行了研究，具有一定的理論意義。

1 材料制備

本文所設計的金屬泡沫復合材料夾芯結構的面板為高強玻璃纖維/環氧樹脂(S2/TDE－85，固化劑為70#酸酐)層合板。它由單層預浸料按一定鋪層角度(45/－45/0/－45/45)手糊鋪設而成，通常00單層用來承受軸向載荷，±450單層用來承受剪切載荷。單層預浸料厚度0.2 mm，纖維體積含量54%，固化度97%。芯子為閉孔鋁泡沫，厚度為10 mm，相對密度0.15，平均孔徑為2 mm左右。單層預浸料和鋁泡沫芯子的力學性能參數見表1。

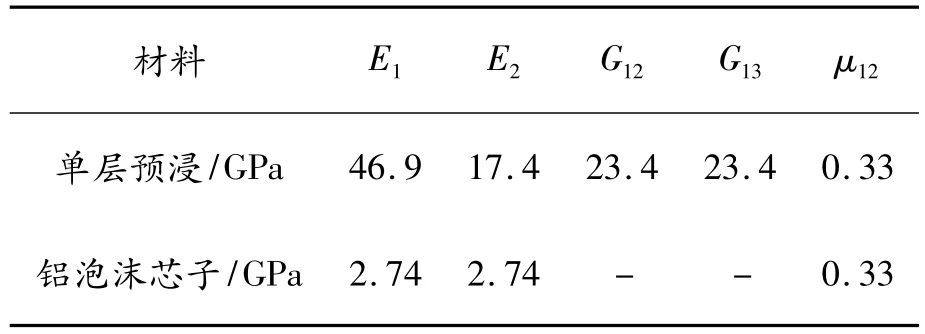
表1 單層預浸料和鋁泡沫芯子的力學性能參數

復合材料層合面板和鋁泡沫芯子采用二次固化方法粘接在一起。具體步驟:將常溫下的膠膜放置在金屬泡沫上;然后將固化后并按試樣尺寸加工的面板置于膠膜之上，將其放置在熱壓機上，加溫加壓，并保持1 h;最后將其取出，常溫下冷卻即成金屬泡沫夾芯結構。膠膜采用J47A，其屬于中溫固化結構膠，可產生較小的翹曲變形和內應力，產品外形精度較高，廣泛用于復合材料二次成型。

2 彎曲試驗

三點彎曲性能實驗參照ASTM C393－06標準［16］進行。試件尺寸為200 mm×60 mm×12.2 mm，每組5個試件。試驗溫度23%，濕度56%，所有試驗均在INSTRON5569型萬能電子試驗機上進行。外伸梁的跨距L為160 mm。加載壓頭為高強度鋼平壓頭，壓頭寬度15 mm。采用位移控制加載，加載速率為2 mm/min，連續加載，計算機自動記錄彎曲載荷和彎曲位移，并繪制載荷－位移曲線。采用奧林巴斯顯微鏡(SZ-STU2)觀察試件破壞模式。為了減少壓頭和試件之間摩擦，在加載壓頭與試件之間墊上一塊硬質橡膠墊片，其寬度大于壓頭寬度，厚度為3 mm。

圖1和圖2分別為芯子厚度10 mm的夾芯結構試件破壞的顯微鏡照片和P－δ響應曲線。

3 分析和討論

3.1 失效模式和曲線分析

由圖1可知，芯子厚度為10 mm的彎曲試件失效模式為面板皺曲。鋁泡沫復合材料夾芯結構的P－δ曲線可分為3個階段(圖2)，即線彈性段、彈塑性段和破壞后的失穩段。在線彈性段，夾芯結構發生線彈性彎曲變形，卸載后變形可以恢復;位移繼續增加，面板內部的薄弱位置達到屈服應力，夾芯梁發生不可恢復的塑性變形，載荷增加的速度變緩。極限載荷以后的失穩段是由于夾芯梁的面板發生皺曲，此時梁的承載能力開始明顯下降。

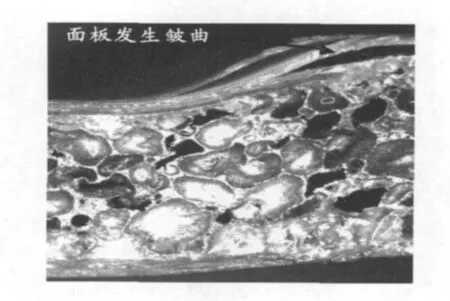
圖1 彎曲夾芯結構試件的破壞微觀照片

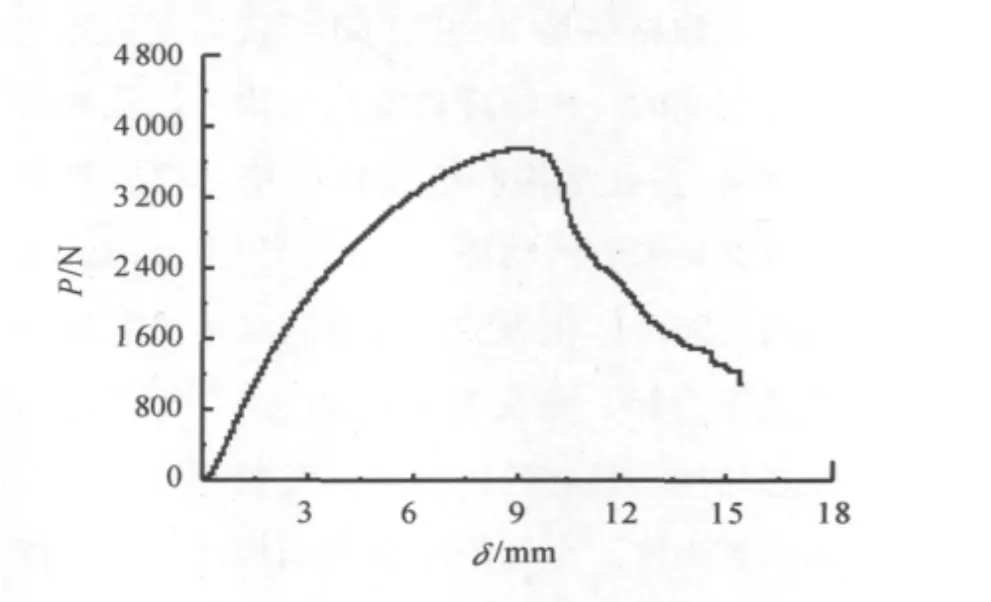
圖2 彎曲夾芯結構試件的的P－δ曲線

3.2 抗彎剛度

圖3為一典型的夾芯梁示意圖，梁中點作用一載荷P，兩端簡支，跨距L。用下角標f和c分別表示面板和芯子，面板厚為tf，芯子厚度為tc，夾芯梁上、下面板形心之間的距離d=tc+tf，夾芯梁寬為b。Ef為面板彈性模量，Ec和Gc分別為芯子彈性模量和剪切模量。

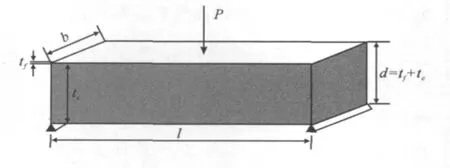
圖3 夾芯梁

梁的抗彎剛度又稱為彎曲剛度，用EI來表示，E為彈性模量，I是面積的二次矩。可用P/δ描述鋁泡沫復合材料夾芯結構的彎曲剛度。P/δ曲線初始直線段的斜率表示夾芯梁的加載剛度。1969年，Allen［17］給出了夾芯梁在三點彎曲載荷下中點撓度δ的計算公式，即

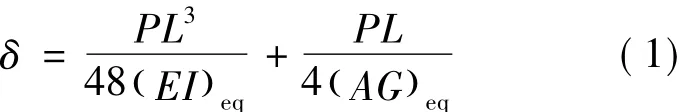
其中:(EI)eq為等效抗彎剛度;(AG)eq為等效剪切剛度。

如果 Ec≤Ef、tf≤tc，則(EI)eq和(AG)eq分別為

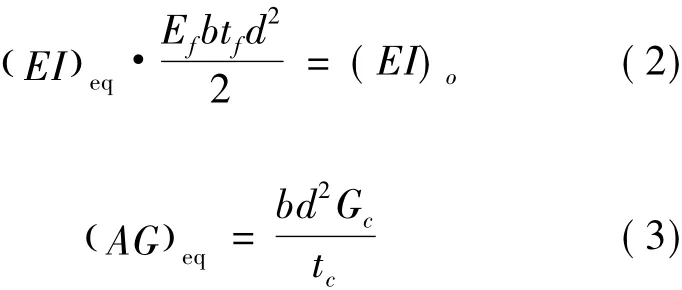
式中Gc為芯子的剪切模量。

將已知各參數代入式(2)，可得到加載剛度理論值。試驗的平均值與理論值見表2。

表2 鋁泡沫夾芯梁的彎曲剛度理論結果與試驗值對比

由表2可知，試驗結果大于理論值，這可能是理論公式中沒有考慮膠層對剛度的貢獻，而且對于芯子為多孔材料的夾芯結構，面板和芯子粘接時，結構膠會滲入與面板相鄰的泡沫孔中形成膠釘，其對剛度也有所貢獻。

3.3 比剛度

文獻［18］指出，一般可用比剛度E1/2/ρ來綜合評價夾芯結構的抗彎特性。其中E為夾芯結構的彎曲彈性模量，ρ為夾芯結構的密度。金屬泡沫夾芯結構的等效彎曲彈性模量為

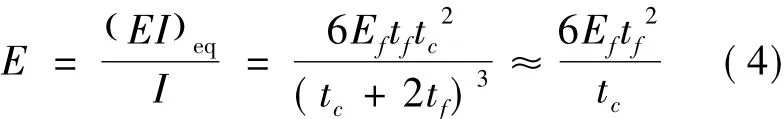
把求解結果和文獻［16］中的3種金屬泡沫夾芯結構進行了對比，結果見表3所示。

由表3可見，與其他3種常見金屬泡沫夾芯結構的彎曲比剛度相比，本文所設計的金屬泡沫復合材料夾芯結構具有較高的彎曲比剛度和明顯的重量優勢，而且復合材料面板具有良好的可設計性，通過對其優化設計，可以提高夾芯結構的比剛度。

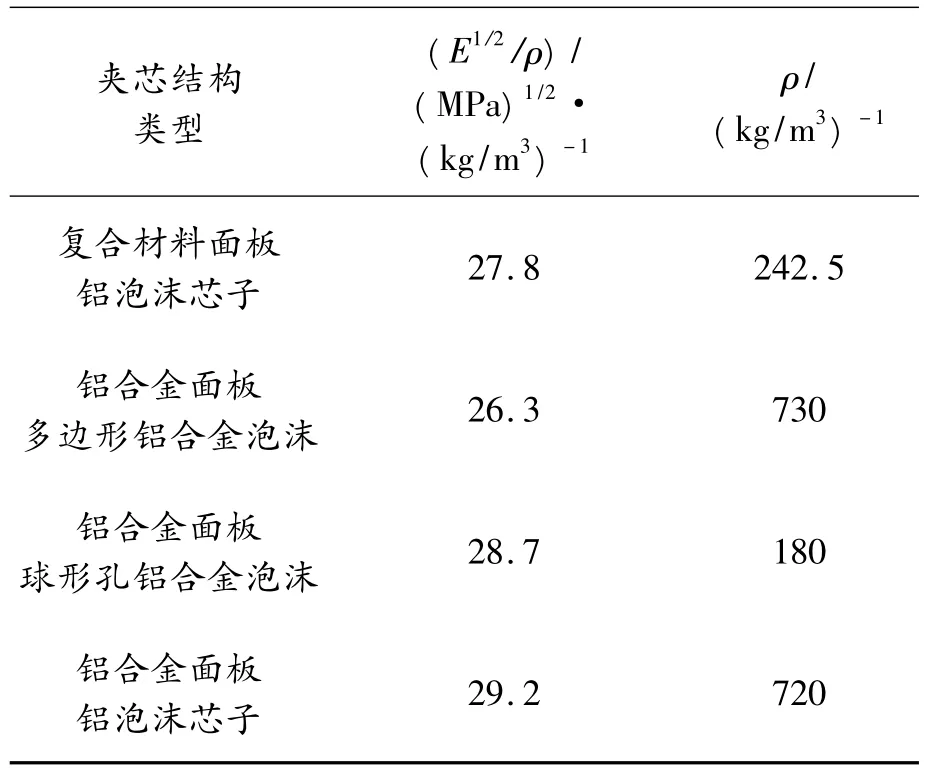
表3 幾種金屬泡沫夾芯結構的比剛度

3.4 失效模式和失效載荷的驗證

將已知各參數帶入文獻［18］各失效模式對應的方程中，可得到各種失效模式下對應的失效載荷，其中最小的失效載荷即為本文所研究的夾芯結構發生失效時的最小載荷值，其對應的失效模式即為該結構的失效形式。鋁泡沫復合材料夾芯梁的尺寸及極限載荷如表4所示。

表4 鋁泡沫夾芯梁的幾何尺寸和極限載荷

由表4可知，在給定幾何參數tf、tc和L以后，鋁泡沫夾芯梁的預測破壞模式與實際破壞模式符合較好，極限載荷理論值高于試驗值，主要原因如下:理論求解是在假設夾芯結構完好的基礎上進行的，但實際上由于制備和加工原因，鋁泡沫夾芯結構內部肯定存在損傷，會使夾芯結構整體性能略有下降。

4 結束語

本文所設計的鋁泡沫復合材料夾芯結構在三點彎曲載荷作用下的失效模式為面板層間脫層。鋁泡沫復合材料夾芯結構的彎曲剛度理論預報值與試驗值吻合較好。與其他3種常見的金屬泡沫芯子金屬面板夾芯結構相比，本文所設計的金屬泡沫復合材料夾芯結構具有較高的彎曲比剛度和明顯的重量優勢及可設計性。鋁泡沫復合材料夾芯梁的預測破壞模式與實際破壞模式符合較好，極限載荷理論值高于試驗值。

［1］Dirk Schwingela，Hans-Wolfgang Seeligera，Claude Vecchionaccib，et al.Aluminium foam sandwich structures for space applications［J］.Acta Astronautica，2007，61:326－330.

［2］John Banhart，Seeliger H W.Aluminium Foam Sandwich Panels:Manufacture，Metallurgy and Applications［J］.Advanced Engineering Materials，2008，10:793 －802.

［3］張林，何德坪.球形孔泡沫鋁合金三明治梁的三點彎曲變形［J］.材料研究學報，2005，19(4):361 －368.

［4］趙龍，何德坪，單鍵.高比強高孔隙率泡沫鋁合金三明治梁［J］.材料研究學報，2004，18(5):485 －493.

［5］尚金堂，何德坪.泡沫層合梁的三點彎曲變形［J］.材料研究學報，2003，17(1):31 －38.

［6］Yu J L，Wang X，Wei Z G，et al.Deformation and failure mechanism of dynamically loaded sandwich beams with aluminum foam core［J］.International Journal of Impact Engineering，2003，28:331 －347.

［7］McCormack T M，Miller R，Kesler O，et al.Failure of sandwich beams with metallic foam cores［J］.Solids and Structures，2001，38:4901 －4920.

［8］Kesler O，Crews L K，Gibson L J.Creep of sandwich beams with metallic foam cores［J］.Materials Science and Engineering A，2003，A341:264 －272.

［9］Kesler O，Gibson L J.Size effects in metallic foam core sandwich beams［J］.Materials Science and Engineering，2002，A326:228 －234.

［10］Tagarielli V L，Fleck N A.A Comparison of the Structural Response of Clamped and Simply Supported Sandwich Beams With Aluminium Faces and a Metal［J］.Journal of Applied Mechanics，2005，72(3):408 －417.

［11］Chen C，Harte A M，Fleck N A.The plastic collapse of sandwich beams with a metallic foam core［J］.Mechanical Sciences，2001，43:1483 －1506.

［12］Harte A M，Fleck N A，Ashby M F.The fatigue strength of sandwich beams with an aluminium alloy foam core［J］.Fatigue，2001，23:499 －507.

［13］Bart-Smith H，Hutchinson J W，Fleck N A，et al.Influence of imperfections on the performance of metal foam core sandwich panels［J］.Solids and Structures，2002，39:4999－5012.

［14］Sha J B，Yip T H.In situ surface displacement analysis on sandwich and multilayer beams composed of aluminum foam core and metallic face sheets under bending loading［J］.Materials Science and Engineering，2004，A386:91－103.

［15］Tagarielli V L，Fleck N A，Deshpande V S.The Collapse Response of sandwich beams with Aluminium Face sheets and a metal foam core［J］.Advance engineering materials，2004，6(6):440 －443.

［16］ASTM Standard C393 －06.2006，Standard Test Method for Core Shear Properties of Sandwich Constructions.Philadelphia［S］.American Society for Testing and Materials.

［17］Allen H G.Analysis and Design of Structural Sandwich Panels［M］.Oxford:Pergamon Press，1969.

［18］Ashby M F，Evans A G，Fleck N A，et al.Metal Foams:A Design Guide［M］.Oxford，UK:Butterworth-Heinema nn，2000.