三次NURBS樣條曲線插補加工螺旋轉子建模與加工研究*

余道洋 韓 江 夏 鏈

(合肥工業大學機械與汽車工程學院，安徽合肥 230009)

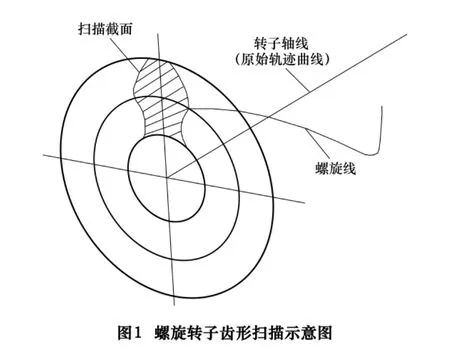
螺旋轉子流量計是20世紀90年代末新推出的一種新型流量計，它具有如下優點:動平衡良好，振動及噪聲小，體積小，計量容量大;不產生脈沖;轉子表面無負荷，在旋轉過程中不產生磨損，使用壽命大大延長［1］。螺旋轉子是其中最關鍵的零件，其端面輪廓齒形截面如圖1所示。

螺旋轉子端面輪廓曲線由3段曲線組成:漸開線、擺線和圓弧。圓弧可以由數控系統圓弧插補來實現，漸開線和擺線現在一般采用微小直線段來擬合實現。但是，微小直線段不僅代碼量非常巨大，而且直線段間的不連續破壞了曲率的光滑性，會導致速度加速度的不連續［2］，存在加工效率低的問題，在四軸加工中心上加工模數為13.5 mm的螺旋轉子需要3 h，加工模數更大的螺旋轉子需要更長加工時間，有的甚至需要20 h以上。要克服這些不足，提高加工效率，必須采用自由曲線插補。本文提出用三次NURBS樣條插補來擬合漸開線和擺線，大大提高了加工效率。

1 三次NURBS曲線構造與計算

1.1 構造三次NURBS曲線

本文以端面輪廓其中擺線段為例，說明三次NURBS曲線的構造過程。三次NURBS曲線可以表示為1個分段有理多項式矢函數。

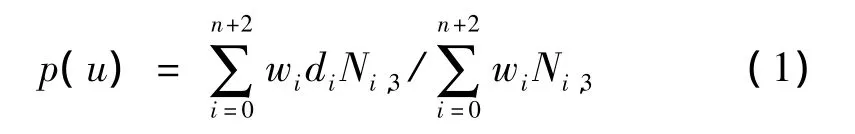
式中:型值點個數為n+1;控制頂點為di(i=0，1，…，n+2)，其順次相連構成控制多邊形;wi為與控制頂點di相對應的權因子;Ni，3是3次B樣條基函數。

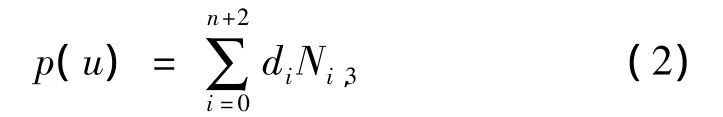
圖2是螺旋轉子端面輪廓曲線擺線上的7個型值點(本文中設n=6)，型值點坐標如表1所示，求通過這些點的三次NURBS曲線。

表1 NURBS曲線上型值點的坐標

1.2 確定節點矢量

根據曲線上的型值點 pi，i=0，1，…，n(n=6)，采用平方根法確定節點矢量。設7維矢量a=(a0a1…a6)，求得a的各個分量如表2所示。

根據式(2)，兩端采用四重節點，構造n+7(即13)維節點矢量

分別在曲線兩端構造4次重節點，即u0=u1=u2=u3;u9=u10=u11=u12，求得各分量的值如表3所示。

1.3 計算基函數

采用 De Boor－Cox遞推算法［3］，

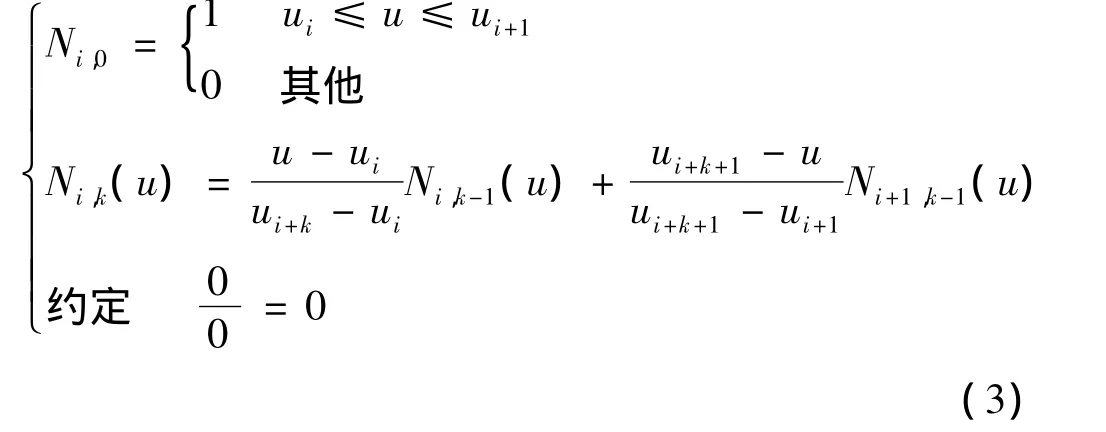
計算時需分別求出0、1、2、3次B樣條基函數，亦即將k=0，1，2，3依次代入公式，通過遞推關系計算得三次B樣條基函數。由于篇幅關系，本文只列出三次B樣條基函數。三次B樣條基函數為:

1.4 反求控制頂點

用于擬合n+1 個型值點pi，i=0，1，…，n的三次B 樣條曲線可表示為［4－5］:

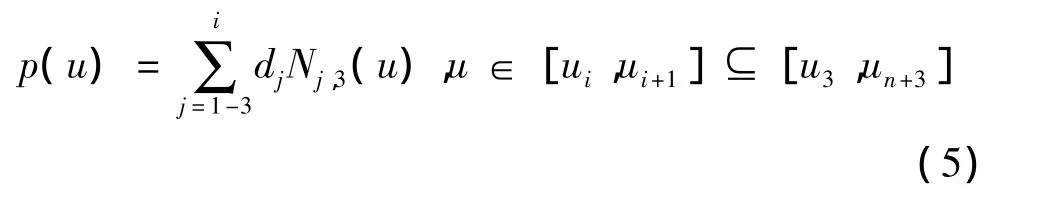
表2 7維矢量a各分量值

表3 節點矢量各分量值

將定義域u∈［u3，un+3］內的節點值依次代入式(5)，有

取n=6，結合邊界條件可求解;設NURBS曲線的控制頂點 d0、d1、d7、d8和NURBS相切，從而可以求出控制頂點的坐標，如表4所示。

表4 控制頂點的坐標

2 計算三次NURBS樣條曲線插補刀位數據

由于大多數高端數控機床都具有刀補功能，計算出三次NURBS樣條曲線的基函數和控制頂點后，可以直接用這些點的數值進行編程［6］。

由式(5)可知:

由1.3節已求出Ni，3，由 1.4節已求出控制頂點的坐標，設i=3時，即u∈［u3，u4］時，可以用三次NURBS樣條曲線來擬合求出螺旋轉子端面輪廓擺線段其中一段:

同理可求出其他幾段，這樣就實現了用三次NURBS樣條曲線來擬合端面輪廓擺線段。

由三次NURBS樣條曲線性質［7］，經過矩陣變換，將式(6)變換成數控系統所需要的三次樣條曲線插補方程，就實現了用三次樣條插補加工螺旋轉子端面輪廓擺線段。

3 刀位數據模擬與誤差分析

將式(6)輸入到Pro/E軟件中，結果如圖3，細線條表示理論擺線輪廓，粗線條是式(6)表示的三次樣條曲線的擬合曲線，經過分析比較三次樣條插補曲線與理論擺線誤差后得出，最大誤差為:0.048 mm，小于螺旋轉子的加工制造允許誤差范圍。同理可以分析比較其他幾個三次樣條曲線的擬合曲線和理論擺線輪廓誤差，經過分析計算，輪廓曲線誤差都在允許的誤差范圍之內。

4 在加工中心上加工驗證

螺旋轉子的實際加工運用立式四軸加工中心進行數控銑削加工。經過實際加工試驗，采用三次NURBS樣條曲線插補加工螺旋轉子，比采用微直線段插補加工螺旋轉子大大提高了螺旋轉子的加工效率，在保證螺旋轉子制造加工精度的前提下，可以提高螺旋轉子的加工效率50%以上。同時，本文采用的三次NURBS樣條曲線插補加工方法對于加工一些特殊曲線和曲面也具有一定的借鑒意義。

［1］余道洋，韓江，夏鏈.螺旋轉子數控加工的數學建模分析與研究［J］.合肥工業大學學報，2007，30(11):1433 －1435.

［2］李建剛，張婷華，李澤湘，等.數控加工中的連續多段直線軌跡B－Spline擬合［J］.哈爾濱工業大學學報，2008，40(10):1606－1608.

［3］施法中.計算機輔助幾何設計與非均勻有理B樣條［M］.北京:高等教育出版社，2001.

［4］王乾廷，桂貴生，劉全坤.三次NURBS曲線輪廓數控加工刀位數據計算［J］.組合機床與自動化加工技術，2003，6:19 －21.

［5］俞芙芳，王乾廷，江吉彬.鞋楦曲面混合有理Bezier構造及刻楦過程仿真［J］.機械工程學報，2005，16(21):1899 －1903.

［6］WANG Yongzhang，CHEN Liangji.A real－ time NURBS surface interpolator for 5 － axis surface machining［J］.Chinese Journal of Aeronautics，2005，18(3):263 －272.

［7］吉貝·德芒熱，讓皮爾·晡熱.曲線與曲面的數學［M］.北京:商務印書館，2000.