數學分析教學中應培養的幾種思想與方法

鮑 芳

（太原大學外語師范學院，山西 太原 030012）

數學分析教學中應培養的幾種思想與方法

鮑 芳

（太原大學外語師范學院，山西 太原 030012）

針對師范院校《數學分析》教學現狀與適應新課程的教師教育改革，提出當前師范院校數學分析課程應體現的數學思想與方法的滲透與教學，這是實現師范院校培養實用型優秀教師的有效途徑。

數學分析；數學思想；數學方法

師范院校承擔著為國家培養未來教師的重任，在大力提倡實施素質教育，培養學生創新能力的今天，師范院校的教學應站在培養具有實際應用能力的人才的高度上來改進教學，用現代教學觀指導教學。對于數學專業而言，要提高本專業的綜合素質，必須培養學生的專業素質即數學素質。數學素質主要是一種數學思維方式，它既包括邏輯思維，也包括從現實生活中提煉數學問題的直覺，形成數學概念的抽象，運用數學語言的能力，構造數學模型的實踐以及運用數學知識去解決問題的意識和能力。《數學分析》是師范數學專業最重要的基礎課之一，其內容豐富，教學垮時長，對學生影響深遠。《數學分析》不僅是學習某些后續課程的基礎，而且在中學數學教學中，如：求切線方程、求極值、判斷函數增減性、證明不等式、求弧長等都具有很大的指導作用，它的基本概念、思想和方法可以說無處不在。因此在教學的每一個環節都要注重數學思想方法的滲透。

1．現狀

師范教育歷經百年，其教育體制和模式有當時的合理性和歷史貢獻，但也應看清它的時代局限。

1.1 教材內容幾乎是純理論敘述，教師在授課時過分注重理論體系而忽視了應用，與社會實際聯系不明顯，很難引起學生的興趣；

1.2 教材內容普遍只見定義、定理、推導、證明，而對思想方法則很少提及，教師在數學分析的教學中只重邏輯思維能力和分析運算能力的培養，輕培養學生解決問題的思想方法能力的培養；

1.3 教師的教學方法單一，教師教育培養模式大多以封閉模式為主，教育理論和教育實踐嚴重脫節，照本宣科，學生提不起興趣。

這些缺陷不利于師范生形成寬厚的知識基礎、良好的職業技能和優秀的綜合素質，制約師范生職后的發展。

2．數學思想

2.1 極限的思想

極限思想是數學分析的精髓， 是用來衡量na和a的接近程度的， 愈小，表示接近得愈好，它除限于正數外，不受任何限制。盡管 有它的任意性，但當一經給出，就應暫時看作固定不變的，即 又有確定性，給定以后，便可根據它來確定N。正是極限概念中扮演主要角色的 的二重性，即 的任意性和確定性，深刻地反映了有限與無限的對立統一的辯證關系，有機地將有限和無限、初等數學與高等數學結合起來。而數學分析中最重要的一些基本概念

例如：設函數 f (x)在區間（ ?a,a）上連續，證明：

2.2 數形結合思想

數形結合的思想，就是充分利用形的直觀性和數的規范性，通過數與形的聯系轉化來研究數學對象和解決數學問題。

分析：如果按課本那樣直接去證明，學生知道了這個等式可用換元法來推導，但是理解起來似乎不那么容易。如果用數形結合的思想方法進行分析，那么結果就很明顯了。

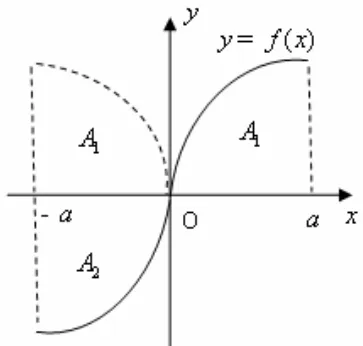
圖1

圖2

在圖1中， f (x)是奇函數， A1表示由 y = f(x)， y =0及圍成圖形的面積， A2表示由 y = f(x)， y =0及圍成圖形的面積，而則

在圖2中， f (x)是偶函數， B1表示由圍成圖形的面積， B2表示由圍成圖形的面積，而

在數學分析中，還有很多結論可用數形結合的思想來解決，如拉格朗日中值定理、閉區間上連續函數的性質、利用積分區域的圖形求重積分等。在教學中可引導學生用數形結合的思想來得出這些結論，這要比純理論證明更好理解。而在中小學數學中，數形結合思想同樣有著廣泛的應用。所以對于師范院校，數學分析課程就要注重培養師范生這種數學思想的形成，這對他們今后的教學將會有很大的幫助。

2.3 數學建模思想

培養學生的數學素質，數學建模是有效的途徑。在信息時代，數學已經不僅僅是一種基礎理論，而且還是一種可以直接產生經濟效益的數學技術，計算機給數學研究和數學教學帶來了深遠的影響。因此，在數學分析教學中，充分利用數學建模的思想來進行教學，對培養學生觀察力、想象力、邏輯思維能力以及分析、解決實際問題的能力都起到了很好的作用。

例如，在引入無窮級數這一個概念時，可以介紹古希臘哲學家芝諾所提出的“阿基里斯追龜悖論”。芝諾的悖論在于他把阿基里斯追烏龜時，烏龜向前爬的距離分成無限段，然后一段一段加以敘述。芝諾認為阿基里斯永遠追不上烏龜，實質就是在無限次追趕中，烏龜向前爬的距離之和為無窮大。在此提出了無限項求和的問題。此前，學生熟知的是有限項求和的概念，如何將有限轉為無限呢?很自然地就用到了極限這一概念。利用已知的有限項求和，結合極限方法，得出了無限項求和的基本方法。這樣的設計不但能更好地引進無窮級數的概念，也能極大地激發學生的興趣。

新課程改革中強調要加強課程內容與學生生活以及現代社會和科技發展的聯系，培養學生分析和解決問題的能力，這就要求師范院校在教學過程中要注意將知識與實際生活多聯系，在數學分析教學中利用建模的思想來培養師范生分析、解決問題的能力就是非常有效的一個途徑。

2.4 轉化的思想

將我們要解決的問題通過轉化為已經解決或者容易解決的問題上來，從而使問題得到解決的思想就是轉化的思想。如海涅定理實現了數列極限與函數極限的轉化，格林公式給出了平面上的第二型曲線積分與二重積分之間的轉化，無窮小與無窮大、廣義積分與級數、重積分與累次積分等都可進行轉化。可見，轉化是數學分析中常用的一種基本思想。

3. 數學方法

數學中有很多常用的方法，如類比推理法、歸納推廣法、猜想發現法等。在解題中，引導學生選取適當的方法解決問題，也是提高學生解題能力的途徑之一，同時還可以促使學生多創新，得出更多的結論。

3.1 歸納推廣

在《數學分析》中，數學概念是比較抽象的，學生往往不明白為什么要這樣來定義，有什么用處，所以在講授數學概念時需要讓學生理解問題是怎樣提出的，概念是如何形成的。在對相關概念進行講授時，可通過案例教學，由學生自己歸納得出。例如，對導數這部分內容，不應只停留在要求學生掌握幾個求導公式，會進行簡單求導上，而應由具有實際背景的實例來引入。導數概念一般是由瞬時速度和切線斜率引入的，當然還可通過研究增長率、膨脹率、效率、密度、加速度、電流強度等反映導數應用的實例來引入，引導學生在實例中歸納出瞬時變化率就是導數。

再如，利用導數討論函數圖像，是大可結合中學實際的。就拿二次三項式的圖像的討論來說，我們知道它的圖像是一拋物線，利用導數知識，從知道當 a > 0 時，曲線開口向上，是凸的，而當 a < 0 時，曲線開口向下，是凹的。當y ' = 2 a x + b = 0時，即處函數有極值

經過這樣簡單的討論，利用導數知識，對二次三項式的圖像的認識就更清楚了。中學數學中許多極值問題的研究，正是依據二次三項式的知識引出的。而導數的知識給予我們一個更有力的方法，它可以推廣到解決更為廣泛的極值問題上來。在這部分的教學中，既要注意把應用導數解決極值問題的一般原理教給學生，同時可選取一些中學課本里的極值問題給學生用新的方法去解決，進行比較，讓學生體會出用導數求極值的方便之處。

3.2 類比推理

類比推理法是指根據兩個問題有一部分特征相類似，從而推出其他特征也可能相類似的一種推理方法。

例如：在講函數極限的概念時，學生理解起來比較困難，但是，學生對數列極限概念比較熟悉。教師在講函數的極限定義時，可與數列極限定義相類比來啟發學生自己給出定義。首先教師指出函數的極限與數列的極限相類似，都是描述在自變量無限增大的過程中，函數值無限接近于一個常數的變化狀態。根據這一特點，可類比數列極限定義來定義函數的極限。接著讓學生找出數列極限與函數極限的對應關系來：最后學生根據這個對應關系很容易得出 f (x) (x→+∞)的定義。這時，教師要向學生說明這種得出定義的方法是類比推理法，在數學分析中有著廣泛的應用，如廣義積分與定積分、格林公式與高斯公式等的類比，并向學生介紹類比推理法的內涵及在數學分析中應用這種方法所得出的一些重要結論，讓學生充分認識到這種方法的重要性。

函數關系式nay= )(xfy=定義域 N ),(+∞a自變量的變化趨勢 ∞→n ∞→x函數值的變化趨勢 aan→ Axf→)(

在教學中還要合理運用啟發式和發現猜想等方法，注重培養學生的創新思維能力、形象思維能力、發散性思維能力等。如在函數凸性的教學中可以使用直觀發現法進行教學，對于萊布尼茲公式，可先讓學生觀察 y ' = u 'v + u v '，

y '' '= ( u''v + 2 u'v '+ u v '' )'= u '''v + 3 u''v '+ 3 u'v '' + u v '''，學生不難發現，上述幾個式子與二項式(u + v )n展開式極為相似，則學生會猜想出，接下來只需用數學歸納法證明這個式子是正確的。對于這個公式的理解，學生通過自己猜想、證明來得出相關結論就要比教師直接證明要有效的多。

培養學生的數學素質，是一項細致而長遠的艱巨任務。教師只有努力提高自身數學思想方法的素養，通過數學教學教會學生數學思想方法，才能有效地提高學生的數學素質，以求達到教育的最終目的——為社會輸送高素質的實用型的教師。

[1] 周煥琴. 論師范數學教育中的素質教育[J]. 安康學院學報，2008，1.

[2] 華東師范大學數學系．數學分析(第三版) [M]．高等教育出版社，2001．

[3] 戴振祥. 數學分析課程如何聯系中學教學的實際[J]. 徐州教育學院學報，2008，3.

[4] 林遠華. 數學分析課程中的數學思想方法研究[J]. 河池師專學報，2001，2.

[5] 譚偉明，李連芬，蘇芳. 數學思想方法與學生數學素養的培養[J]. 梧州學院學報，2009，6.

[6] 樊仲光. 新升本科院校數學分析教學的幾點思考[J]. 廣西教育學院學報，2010，2.

G42

A

1008-7427（2011）03-0123-02

2010-12-31

山西省教育科學規劃課題，項目編號：GH-09228；太原大學外語師范學院教育科學研究課題，項目編號：XYYL-011。