超長混凝土結構溫度應力分析

中國建筑東北設計研究院 栗樹文

超長混凝土結構溫度應力分析

中國建筑東北設計研究院 栗樹文

現代建筑業中出現了越來越多體量巨大的建筑，其長度可達100～200m。規范規定：超過55m的框架結構應在其中部設置若干溫度伸縮縫。但常常由于使用功能和構造上的要求，不適宜在建筑結構中設縫斷開，因此不設縫的設計思想被越來越多的設計人員所認同。一般來說，結構越長，溫度及收縮變形就越大，約束內力也就越大，往往引起結構開裂，影響其正常使用，此時超長混凝土的溫度應力分析成為設計中的一個重要環節。溫度作用（收縮）應力（內力）的計算與外荷載作用下的主內力計算不同，其值的大小取決于支撐形式及其抗側移剛度，且兩者互為因果關系。

一、溫度應力計算原理

實際結構在環境溫度作用下的應力分布、開裂形態是一個時變的、非線性的復雜問題，環境溫度變化時，結構兩側分別向內收縮或向外膨脹，在結構的平面剛度形心附近存在一個不動點。距離不動點越遠的地方，產生的變形越大。以圖1所示的框架結構為例，在沒有柱子約束的條件下，第i根柱子處的變形計算公式為：

式中，i為不動點為基準的柱子序號，l為框架跨度，Δt1為與混凝土成型時的環境溫度相比較的變化量,αT為混凝土的熱脹系數，一般為1×10-5m/(m·℃)。

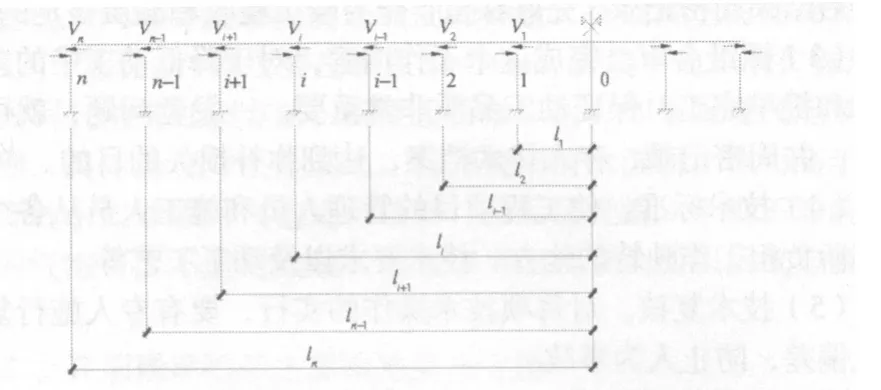
圖1 某榀超長框架示意圖

當樓蓋與柱子整澆在一起時，樓蓋的變形會帶動柱子產生側向位移。如果柱的上下端位移一致，柱子中將不產生內力。顯然，為了協調這一變形，柱子上會產生剪力、彎矩等內力。這些因素相互作用，使實際各支撐柱處產生的變形比式（1）計算的略小。因此，如果柱頂、柱底處于不同的環境溫度時，第i根柱子的剪力Vi可以由下式得出：

式中，Δt為柱子上下端所處的環境溫度差；D為柱抗側移剛度，根據結構力學公式，可得到D=12EcIc/ H3，式中H為柱子高度；Ec、Ic為柱子的彈性模量、慣性矩。而樓蓋中的平均拉應力為：

式 中，Nj為不動點起第j跨的樓蓋軸力，A為樓蓋橫截面面積。柱子的剪力同時將引起彎矩，其峰值為：

式中，β為反彎點距離柱頂、柱底的距離與柱子高度的比值。

此彎矩由與柱子相連的框架梁（包括翼緣板）承擔，對于頂層樓蓋，中柱情況下，兩側梁剛度基本一致，彎矩由左右梁平均分配這一彎矩，而對于邊柱，這一彎矩僅由一根梁平衡，因此，與中柱、邊柱相連梁的最外層纖維所受到的彎矩拉應力分別為：σM,中=βHVj/ 2W，σM,邊= βHVi/ 2W。可以預見，這一拉應力同時也會影響作為翼緣的樓板應力。

二、多層框架結構溫度應力的特點

溫度應力實際上是一種約束應力，約束應力包括內約束應力和外約束應力。引起溫度應力的溫度荷載一般可分為季節溫差、驟然溫差和日照溫差等，長期緩慢的季節溫度變化作用于結構整體，對結構的變形影響較大，依據大量的實踐經驗，多層鋼筋混凝土框架結構的溫度應力計算有如下特點。

1. 假定基礎上地下室不變形，多層框架按兩層計算（只考慮地面以上兩層框架，頂層計算時只考慮頂部兩層框架）。

2. 多層框架的最不利部位是變形不動點的橫梁，此處承受著最大的軸拉力（收縮時）。假定是對稱結構，結構中間部位橫梁可能開裂，并且在下部1、2層開裂較嚴重；端部柱子承受著最大的彎矩和剪力，可能出現主根彎曲和剪切破壞，如圖2、圖3所示。

3. 多層框架中間部位橫梁內力最大，變形最小，端部內力最小，變形最大。

圖2 降溫時典型框架的彎矩

圖3 降溫時典型框架的軸力（梁）和剪力（柱）

三、溫度應力對樓板的影響

溫度作用引起的板中應力可分為兩部分，其一為軸向拉力引起的拉應力，其沿樓板橫向截面基本均勻分布，沿樓板厚度方向也基本均勻分布，危害較大。其二為彎矩引起的拉應力，其引起的拉應力不會形成貫通裂縫，同時，開裂后內力將會發生重分布，由未開裂部分承擔內力，影響要小得多。需要注意的是，溫度作用下的彎曲應力將會與正常使用下的荷載作用相疊加，在不利組合下，會加劇、加速裂縫的發生和發展，特別是梁的支座截面。

四、結論

通過對溫度作用的理論分析，可以得出如下結論。

1. 豎向構件的抗側剛度對超長結構溫度應力影響很大，剛度越大，受溫度作用影響就越大。

2. 溫度作用中存在一個“不動點”，距離不動點越遠，豎向構件的受力就越大；越近，水平構件的受力就越大。

3. 超長混凝土結構受降溫影響較大，升溫作用對結構無太大影響。

4. 計算溫度作用時，可以僅考慮地面以上兩層或頂部兩層，中間層溫度作用基本可以忽略不計。

5. 板中會產生均勻的拉應力和局部的彎曲拉應力，一般情況下均勻拉應力對板影響較大，可能產生貫通裂縫，但在某些情況下局部彎曲拉應力會大于平均拉應力，其影響不容忽視。