可靠度理論在隧道襯砌結(jié)構(gòu)設(shè)計(jì)中的應(yīng)用

陜西鐵路工程職業(yè)技術(shù)學(xué)院 高攀科

可靠度理論在隧道襯砌結(jié)構(gòu)設(shè)計(jì)中的應(yīng)用

陜西鐵路工程職業(yè)技術(shù)學(xué)院 高攀科

可靠度理論在工程結(jié)構(gòu)設(shè)計(jì)中的應(yīng)用從20世紀(jì)40年代開始。我國(guó)從20世紀(jì)50年代開展了極限狀態(tài)設(shè)計(jì)方法的研究工作，20世紀(jì)50年代中期，采用了前蘇聯(lián)提出的極限狀態(tài)設(shè)計(jì)方法。20世紀(jì)60年代，土木工程界廣泛開展結(jié)構(gòu)安全度的研究與探討。20世紀(jì)70年代開始在建筑結(jié)構(gòu)領(lǐng)域開展可靠度的理論和應(yīng)用研究工作，并把半經(jīng)驗(yàn)半概率的方法應(yīng)用到工業(yè)與民用建筑、水利水電工程、港口工程、公路工程和鐵路橋梁等6種有關(guān)結(jié)構(gòu)設(shè)計(jì)的規(guī)范中。目前，我國(guó)以可靠度理論為基礎(chǔ)修訂鐵路隧道設(shè)計(jì)規(guī)范的工作取得了重大進(jìn)展，并完成了新的《鐵路隧道設(shè)計(jì)規(guī)范》（JB10003—99），其機(jī)構(gòu)采用“荷載—結(jié)構(gòu)”模式。

在隧道建設(shè)理論中，隨著巖石力學(xué)的發(fā)展和錨噴支護(hù)的應(yīng)用，逐漸形成了以巖石力學(xué)理論為理論基礎(chǔ)的，支護(hù)與圍巖共同作用的現(xiàn)代支護(hù)結(jié)構(gòu)原理。當(dāng)前國(guó)際上廣泛流行的新奧地利隧道設(shè)計(jì)施工方法，就是基于這一支護(hù)原理。本文，筆者簡(jiǎn)述了用隨機(jī)有限元對(duì)隧道錨噴支護(hù)結(jié)構(gòu)進(jìn)行分析的基本方法和過程，在現(xiàn)場(chǎng)勘察資料還比較欠缺的情況下，按概率及數(shù)理統(tǒng)計(jì)原理，利用蒙特卡洛法（Monte—Carlo），通過計(jì)算機(jī)對(duì)隨機(jī)變量取樣，然后對(duì)某隧道二次模注混凝土襯砌的承載能力極限狀態(tài)可靠度作了初步評(píng)估。

一、蒙特卡洛法簡(jiǎn)介

當(dāng)前在工程實(shí)踐中均采用可靠指標(biāo)β作為構(gòu)件或結(jié)構(gòu)可靠度的度量指標(biāo)：

其中，μZ、σZ為構(gòu)件的均值和標(biāo)準(zhǔn)方差。

若要得出結(jié)構(gòu)的可靠指標(biāo)β，首先應(yīng)求得構(gòu)件抗力R、荷載效應(yīng)S的統(tǒng)計(jì)特征μR、μS、σR、σS，就必須有大量用于計(jì)算的原始幾何與物理力學(xué)參數(shù)，但由于現(xiàn)場(chǎng)地質(zhì)勘察資料還不充足，為此，采用較為簡(jiǎn)單且精度較高的Monte—Carlo試驗(yàn)法。Monte—Carlo法對(duì)結(jié)構(gòu)工程中不確定性的統(tǒng)計(jì)分析，特別是對(duì)于那些通過非線性方程來表達(dá)數(shù)量很多的隨機(jī)變量之間關(guān)系的問題，是一個(gè)行之有效的工具。

該方法的基本原理是：首先對(duì)各基本隨機(jī)變量X通過計(jì)算機(jī)進(jìn)行隨機(jī)抽樣，分別獲得其分位值x1，x2，…，xn。利用隨機(jī)函數(shù)產(chǎn)生（0，1）之間的均勻分布隨機(jī)數(shù)u1，u2；將u1，u2轉(zhuǎn)換為標(biāo)準(zhǔn)正態(tài)分布隨機(jī)數(shù)r1，r2；將標(biāo)準(zhǔn)正態(tài)隨機(jī)數(shù)r1，r2轉(zhuǎn)換為基本變量實(shí)際分布隨機(jī)數(shù)xi。其次，根據(jù)所得X的大量樣本求出X的統(tǒng)計(jì)μx、σx、δx，并用假設(shè)檢驗(yàn)方法求出X的概率分布。

二、可靠度分析

由于坍方段的覆蓋層薄、圍巖松散破碎，地表滲水對(duì)洞身圍巖的穩(wěn)定性影響大，且洞身中、下部及仰拱開挖支護(hù)擾動(dòng)時(shí)會(huì)進(jìn)一步影響其穩(wěn)定性，故必須對(duì)地表坍腔及坍塌體、洞內(nèi)坍口及相鄰初期支護(hù)段進(jìn)行緊急加固處理，防止坍方的進(jìn)一步擴(kuò)大。具體實(shí)施簡(jiǎn)述如下。

1.建立分析模型。筆者在對(duì)圍巖與襯砌結(jié)構(gòu)相互作用機(jī)理的處理上采用主動(dòng)荷載加圍巖彈性約束的模型。此模型認(rèn)為在非均勻分布的主動(dòng)荷載作用下，襯砌結(jié)構(gòu)的一部分將發(fā)生向圍巖方向的變形，只要圍巖具有一定的剛度，就必然會(huì)對(duì)襯砌結(jié)構(gòu)產(chǎn)生彈性抗力以抑制它的變形；襯砌的另一部分則背離圍巖向著隧道內(nèi)變形，不產(chǎn)生彈性抗力，形成所謂的脫離區(qū)。如圖1所示。

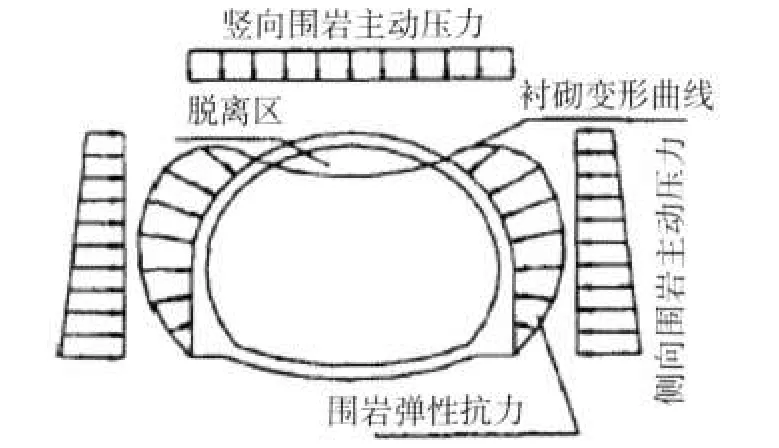
圖 1 圍巖與襯砌結(jié)構(gòu)相互作用機(jī)理模型

2.模型求解。由上述分析可知，襯砌結(jié)構(gòu)的內(nèi)力分析是個(gè)非線性問題，須采用迭代或某些線性化的假定：轉(zhuǎn)換成超靜定結(jié)構(gòu)求解。并將它簡(jiǎn)化成一個(gè)平面應(yīng)變問題。根據(jù)結(jié)構(gòu)力學(xué)原理，把襯砌結(jié)構(gòu)離散成50個(gè)梁柱單元，單元之間采用剛性節(jié)點(diǎn)聯(lián)結(jié)，在節(jié)點(diǎn)上安設(shè)只承受壓力的彈性支座，各單元編號(hào)順序如圖2所示（根據(jù)對(duì)稱性，圖中僅給出半跨的情況）。用矩陣位移法進(jìn)行求解。

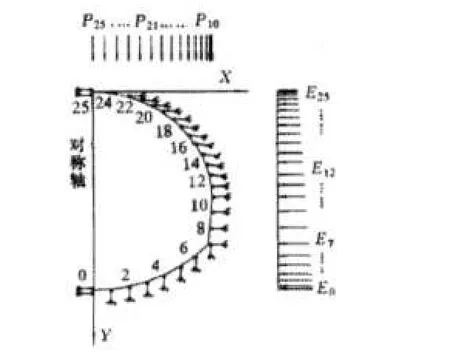
圖 2 襯砌單元編號(hào)示意

3.利用Monte—Carlo法計(jì)算參數(shù)。計(jì)算時(shí)把圍巖容重γr側(cè)壓力系數(shù)λ、垂直荷載高度（或埋深）hq、圍巖的彈性抗力系數(shù)Kr、襯砌結(jié)構(gòu)的彈性模量Ec、混凝土容重γc、結(jié)構(gòu)的厚度d以及混凝土的抗拉強(qiáng)度fcl與抗壓強(qiáng)度fca等幾何與物理力學(xué)參數(shù)均當(dāng)作隨機(jī)變量，對(duì)以上各參數(shù)采用蒙特卡洛法，由此得出襯砌的相關(guān)位移與內(nèi)力的均值和方差，并計(jì)算出襯砌結(jié)構(gòu)的可靠指標(biāo)。

三、工程實(shí)例

分析了某隧道襯砌篩選的3種斷面：?jiǎn)涡膱A、坦三心圓和尖三心圓在Ⅴ級(jí)圍巖（淺埋）荷載作用下，二次模注混凝土襯砌的可靠度進(jìn)行了計(jì)算分析（圖3為推薦的單心圓斷面形式）圍巖與襯砌結(jié)構(gòu)各隨機(jī)變量統(tǒng)計(jì)特征結(jié)果見表1（僅列Ⅴ級(jí)圍巖的統(tǒng)計(jì)結(jié)果）。從表1中數(shù)據(jù)可以看出，與圍巖荷載有關(guān)的計(jì)算參數(shù)多呈對(duì)數(shù)正態(tài)分布，而與襯砌幾何、力學(xué)性能有關(guān)的指標(biāo)側(cè)均呈正態(tài)分布。而襯砌厚度d的變化范圍也大致能反映洞室開挖后內(nèi)輪廓的凹凸不平。

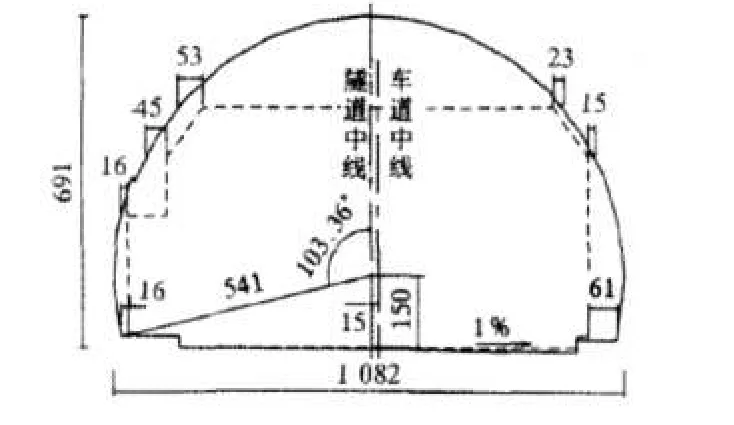
圖 3 隧道內(nèi)輪廓優(yōu)化單心圓（cm）

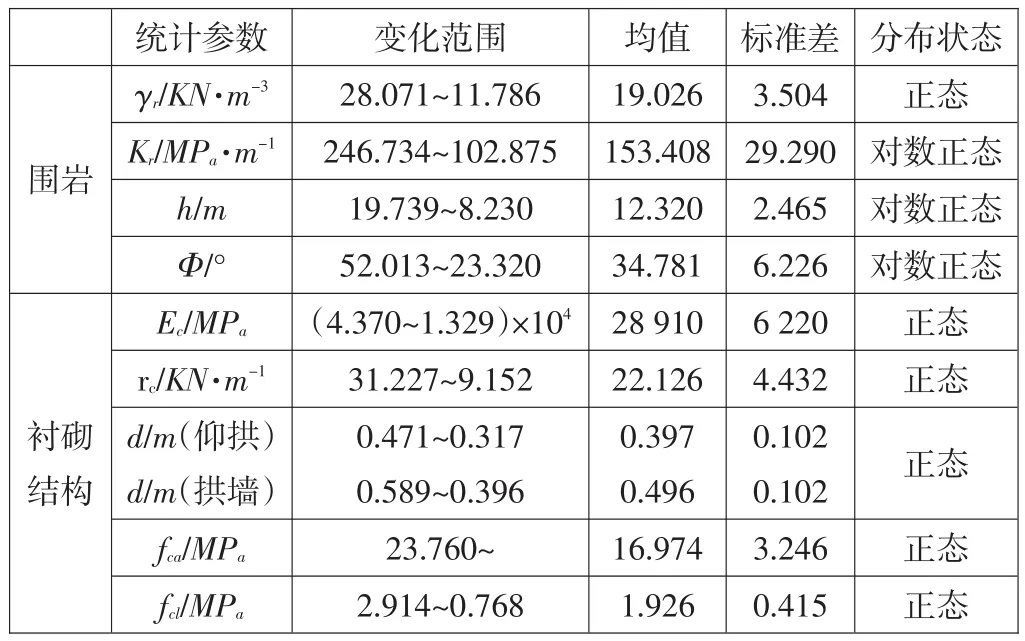
表 1 Ⅴ級(jí)圍巖與襯砌結(jié)構(gòu)各隨機(jī)變量統(tǒng)計(jì)

為便于分析，將襯砌結(jié)構(gòu)的可靠指標(biāo)計(jì)算結(jié)果中幾個(gè)具有可比性的關(guān)鍵部位，如邊墻腳、最大跨度處、限界高度為4m處、拱腰、拱頂以及最小的可靠指標(biāo)列于表2進(jìn)行比較。根據(jù)《鐵路隧道設(shè)計(jì)規(guī)范》襯砌結(jié)構(gòu)截面目標(biāo)可靠指標(biāo)β值在承載能力極限狀態(tài)時(shí)取3.7，正常使用極限狀態(tài)時(shí)取1.0。結(jié)果表明只有拱頂和邊墻局部的值β小于3.7，但都大于1.0。

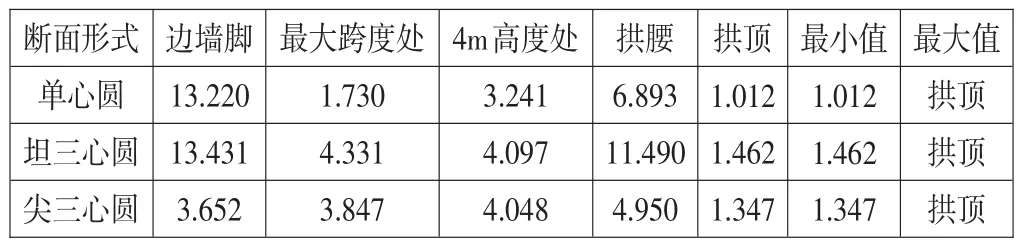
表 2 Ⅴ級(jí)圍巖淺埋3種斷面主要部位可靠度指標(biāo)β值

四、結(jié)論

通過蒙特卡洛法對(duì)該隧道襯砌結(jié)構(gòu)進(jìn)行了承載能力的可靠度分析，得出了以下一些結(jié)論。

1.就整體襯砌結(jié)構(gòu)的力學(xué)性能與施工時(shí)洞室開挖的穩(wěn)定性而言，單心圓最佳，尖三心圓次之，坦三心圓最差。

2.在Ⅴ級(jí)圍巖地段仰拱厚度宜適當(dāng)增加（≥40cm）。Ⅴ級(jí)圍巖深埋地段亦應(yīng)設(shè)計(jì)仰拱。

3.單心圓襯砌結(jié)構(gòu)大部分截面都能滿足承載能力極限狀態(tài)時(shí)的受力要求，雖然還存在局部截面的可靠指標(biāo)不能達(dá)到“理想值”，但不會(huì)導(dǎo)致結(jié)構(gòu)整體失效。工程實(shí)踐證明，只有當(dāng)襯砌的拱圈或邊墻的大部分部位失效時(shí)，襯砌結(jié)構(gòu)才會(huì)失去承載能力。