隨機信息中正態方差的灰色估計
李勇
(重慶工商大學數學與統計學院,重慶400067)
隨機信息中正態方差的灰色估計
李勇
(重慶工商大學數學與統計學院,重慶400067)
利用隨機信息進行參數估計,是數理統計學的基本內容。但經典統計學的理論和方法,都是建立在參數是明確數據的基礎上。而現實社會經濟生活中的參數,具有大量不確定性或認識的模糊灰色性。文章在Neyman的置信區間理論基礎上,借助灰色系統的方法,在隨機樣本的信息下,對正態方差的灰色估計進行了研究,求出了正態方差的灰數估計及其白化權函數;并列舉實例以示其應用。
隨機信息;正態方差;灰色估計
1 灰數的定義
灰色系統理論是1982年鄧聚龍提出的,是處理少數據不確定性問題的理論。少數據不確定性即稱灰性。而灰統計是指將統計對象的實際樣本通過白化權函數抽象為數字量(即灰統計量),按此灰統計量統計出對象所屬灰類的權。
灰數指只知道大概范圍而不知其確切值的數,常指某個區間或某個一般數集內取值的不確定數。本文的灰數主要指三角形(態)的區間灰數?∈[a,b],灰數的白化值記為=ax+(1-x)b,x∈[0,1],灰數的白化權函數主要指三角形(態)(適中測度)白化權函數,其一般形式為:
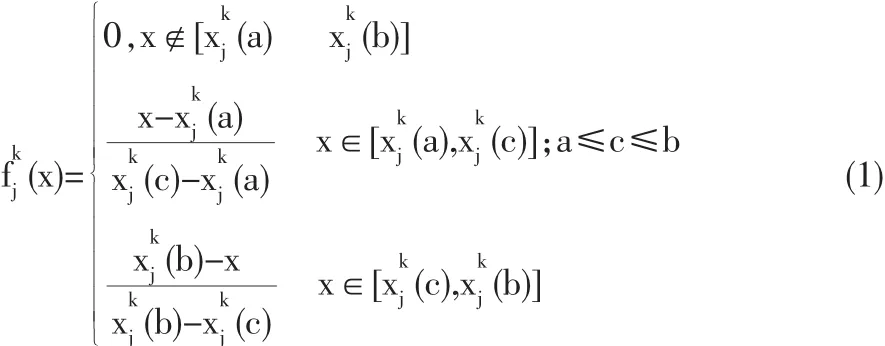
2 灰色估計
灰色估計是指使用灰數作為概率密度函數或離散的概率質量函數的參數估計值。首先,利用Neyman的置信區間理論,來獲得作為參數估計值的灰數。令X為隨機變量且f(x,θ)(θ為參數)為其概率密度函數或概率質量函數。設隨機樣本x1,…xn,令Y=μ(x1,…xn)是用以估計參數θ的統計量,在給定隨機變量值為Xi=xi,1≤i≤n的情形下,能得到θ的點θ*=y=u(X1,…,Xn)。從而得參數θ的(1-β)100%的置信區間,其中β值取為0.01。
其區間表示為:

在(2)中,0.01≤β≤1,當β=1時,即為0%置信區間,此時以點估計值θ*的[θ*,θ*]表示置信區間。


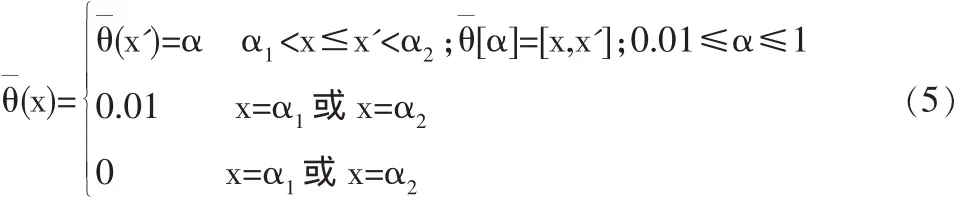
3 正態方差的灰色估計
設X是一個服從正常分布N(μ,σ2)的隨機變量,μ和σ2都是未知參數。現隨機抽取一組來自N(μ,σ2)的隨機樣本X1,……,Xn,估計其參數σ2。設這組隨機樣本值為x1,…,xn,則未知參數σ2的點估計值可表示如下:

又由于(n-1)s2/σ2服從自由度為n-1的卡方分布,因此:
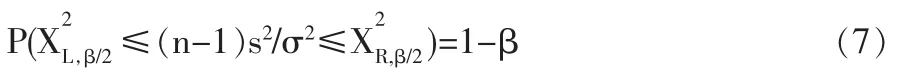

根據上述討論,利用正態方差σ2的(1-β)的置信區間對正態方差σ2進行灰色估計。設正態方差σ2的灰色估計數為是三角形(態)區間灰數。在當0.01≤β≤1時,正態方差σ2的灰色估計數為的白化權函數(x)為:
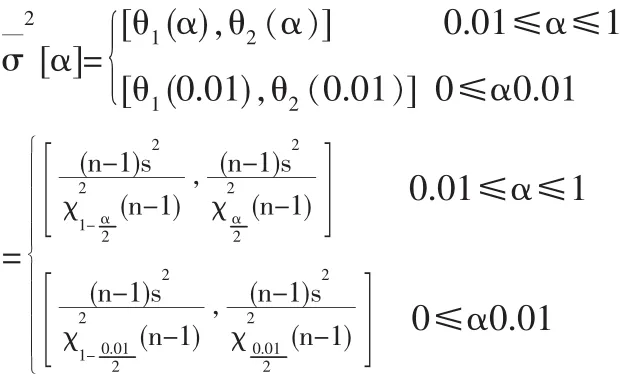
且α1=θ1(0.01),α2=θ2(0.01)。
4 應用實例
例:為了比較不同國家或地區之間的真正實際生活水平,不能簡單地利用貨幣來計算,需要利用“購買力平價”(簡稱PPP)方法來測度。假定根據“PPP”方法測算的重慶市一地區人均月收入(元)X服從正態分布N(μ,σ2),其總體均值μ和σ2未知。現根據簡單隨機抽樣獲得一組來自該總體的有效隨機樣本X1…,X121,樣本均值為2658元,樣本方差為1000。在置信水平99%下,求該正態總體方差σ2的灰色估計。
解:由(8)得,σ2的99%置信區間為:

則可求得該總體方差σ2的灰色估計數,灰數的白化權函數為:

5 結論
利用隨機信息進行參數估計,是數理統計學的基本內容。但經典統計學的方法,都是建立在參數是明確數據基礎上的參數估計理論和方法。而現實社會經濟生活中的大多數參數,具有不確定性或認識的模糊灰色性。本文在Neyman的置信區間理論基礎上,借助于灰色系統的方法,研究了在隨機樣本的信息下,對正態方差的灰色估計研究,這比點估計或Neyman的置信區間能夠提供相對多的有效信息。
[1]陳希孺.數理統計引論[M].北京:科學出版社,1981.
[2]李勇,張維,陳正偉.隨機樣本中正態均值的灰色區間估計研究[J].統計與決策,2010,(13).
[3]劉思峰,黨耀國,方志耕等.灰色系統理論及其應用(第5版)[M].北京:科學出版社,2010.
[4]James J.Buckley.Fuzzy Statistics[M].Berlin:Springer-Verlag,2004.
C32
A
1002-6487(2011)07-0024-02
國家社會科學基金資助項目(09XTJ002);國家自然科學基金資助項目(10871217)
李勇(1970-),男,重慶人,博士,研究方向:統計學理論及應用。
(責任編輯/浩天)

