基于非線性動力系統的我國CPI和PPI非線性關系研究

鄧月明，李興緒

（云南財經大學統計與數學學院，昆明650221）

基于非線性動力系統的我國CPI和PPI非線性關系研究

鄧月明，李興緒

（云南財經大學統計與數學學院，昆明650221）

文章根據我國2002年1月～2009年10月CPI和PPI的月度數據，應用非線性動力學的方法，建立了非線性動力系統（C-PNLDS）模型，來揭示我國CPI和PPI的非線性關系。結果表明：CPI具有自我增長機制，PPI對CPI有加速抑制的影響；PPI也具有自我增長機制，CPI自身對PPI的增長有抑制作用，但它的平方項加速了PPI的增長；耦合項對CPI無影響，而使PPI受損，所以二者是共棲（偏害）的關系。

CPI；PPI；非線性動力系統模型

0 引言

居民消費價格指數簡稱CPI，是度量一組代表性消費商品及服務價格水平隨著時間而變動的相對數，反映居民家庭購買的消費品及服務價格水平的變動情況。生產者價格指數的簡稱PPI，在這里特指工業品出廠價格指數。工業品出廠價格指數是反映全部工業產品出廠價格總水平的變動趨勢和程度的相對數[1]。

居民消費價格指數（CPI）和工業品出廠價格指數(PPI)有著各自的計算方法和用途，但二者之間又存在著密切的聯系。分析清楚二者之間的關系，可以對我國的居民消費情況、工業品內部結構以及經濟運行情況作出基本的判斷，對宏觀經濟政策的制定起著重要的作用。

那么二者究竟是什么關系？是CPI變動帶動PPI變動？還是PPI變動帶動CPI變動？誰決定誰？很多專家學者可謂是見人見智，研究方法也有很多。

研究CPI與PPI關系的方法歸結起來有線性回歸分析、格蘭杰因果檢驗、誤差修正模型、協整檢驗和VAR（向量自回歸）模型，這些方法揭示的都是CPI與PPI線性的關系，但是在復雜、現實的經濟體系中，二者之間的關系很可能是非線性的。本文將選取我國2002年1月～2009年10月的CPI和PPI月度數據，用動態計量經濟學的方法建立CPI和PPI的離散型非線性動態模型，再轉化為CPI-PPI非線性動力系統（C-PNLDS）模型來分析CPI與PPI之間的非線性關系。

1 非線性動力系統（C-PN LDS）模型的建立

1.1 廣義Lotka-Volterra模型介紹

Lotka-Volterra模型最早是由美國生態學家Lotka和意大利數學家Volterra為模擬一些生態現象而提出來并進行研究的,這個模型又稱為捕食者被捕食者模型或弱肉強食模型。生物群體中的兩個物種通過一定的相互作用進而形成的關系是最簡單的動力學系統。兩個物種之間的相互關系可能是相互獨立，也可能是相互競爭，或者是相互促進。

羅納德·肖恩[2]給出了廣義Lotka-Volterra模型，這個模型的標準形式為：

在上述模型中a和b是一次變量反饋系數，如果a和b是正數，x和y回自然增長，反之則會自然下降；c和d是二次變量反饋系數，如果c和d是正數，則x和y回加速增長，反之則會發生阻塞現象；e和f是耦合項xy的系數。當模型（1）用于研究兩個變量之間的關系時，根據e和f的符號，可以得出x和y的9種相互作用的關系（見表1）。

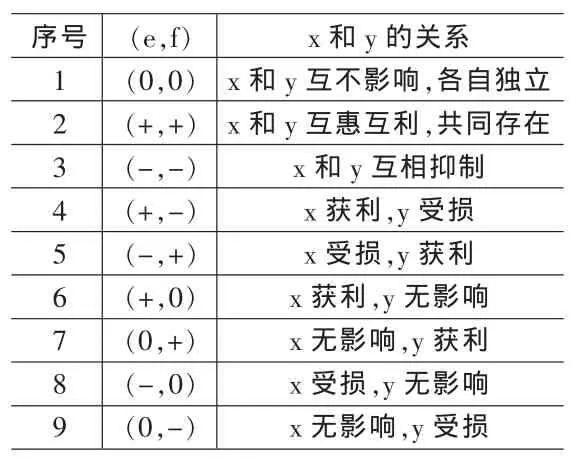
表1 兩個變量相互作用的關系特征表

1.2 非線性動力系統（C-PNLDS）的基本假設

假設1系統性。C-PNLDS是在不考慮其他變量影響的情況下由CPI和PPI非線性相互作用而形成的具有一定結構和功能的整體。

假設2連續性。C-PNLDS是一個連續系統，CPI和PPI都是時間的連續函數。

假設3可差分性。本質上C-PNLDS是一個連續系統，然而直接建立并求解一個微分方程比較困難。所以把C-PNLDS作為一個離散的可差分系統，就可以根據統計數據建立差分方程組進行計算，再轉化為微分方程組。

假設4確定性。C-PNLDS難免受到隨機因素的干擾，但只要隨機干擾因素是平穩的，就可以不考慮隨機因素的影響，而只考慮C-PNLDS中的確定性關系。

1.3 非線性動力系統（C-PNLDS）模型

從模型（1）的表達形式可以明顯的看出來，廣義Lotka-Volterra模型，x和y的相互影響只是通過耦合項xy間接發生，但從實際情況來考慮CPI可能直接影響PPI的增長或減少，甚至是加速PPI的增長或減少；反過來PPI也可能直接影響CPI的增長或減少，甚至是加速CPI的增長或減少。同時，CPI和PPI具有明顯的時間趨勢，還可能有顯性的時間變量。因此，把廣義Lotka-Volterra模型進一步擴展為CPNLDS模型：

模型（2）為非線性動力系統。若m、n不顯著，則為自治平面非線性動力系統，為CPI和PPI的最高冪次不超過二次的系統演化方程。a、b、c、d、e、f、g、h、i、j、m、n為系數，當系數取不同值時，C-PNLDS有以下幾種特殊情況：

(1)e、f、g、h、i、j、m、n均為0，則表示CPI和PPI是兩個獨立發展的系統，具有自我演化的動力機制。當a、b大于0時則表示CPI、PPI兩個系統自我增長；當a、b小于0時則表示CPI、PPI兩個系統自我抑制；當c、d大于0時則表示CPI、PPI兩個系統具有加速發展機制；當c、d小于0時則表示CPI、PPI兩個系統具有減速發展機制，具有阻塞因素。

(2)如果g、h、i、j大于0，則CPI和PPI之間具有互助關系，其中i、j為加速度系數；如果g、h、i、j小于0，則CPI和PPI之間具有互抑關系，其中i、j為減速度系數。

(3)如果e、f大于0，表示CPI和PPI之間產生協同效應，CPI和PPI之間為互惠關系；如果e、f小于0，則表示CPI和PPI之間具有競爭關系；如果e、f一正一負，則表示CPI和PPI之間具有捕食關系；如果e、f有一個為0，則表示CPI和PPI之間具有共棲關系。

(4)如果c、d、e、f、i、j等于0，則C-PNLDS為非自治的線性系統，當m、n也等于0時，C-PNLDS為自治的線性系統，其實就是一階循環式結構模型。

(5)如果a、b大于1，且e、f、g、h、i、j、m、n大于0，則CPI和PPI互為因果關系，相互促進，產生協演化。這是一種最理想的關系。

在這里直接估計模型（2）是很困難的，因為模型（2）中的方程是非線性的微分方程，其中平方項和耦合項是強非線性項，難于確定函數關系。所以，在這里我們采用的是對離散的非線性差分模型的參數進行估計，模型的形式為：

在模型（3）建立好之后，我們要對其進行參數估計，并對u1、u2進行EG平穩性檢驗，如果通過了檢驗，則表明模型（3）中的變量之間存在協整關系。并且在可決系數很高的情況下，模型（3）可以近似的轉化為C-PNLDS模型，即模型（2）。這樣我們通過對模型（3）的參數進行估計，進而得到模型（2）的參數。

2 實證分析

本文選取我國2002年1月～2009年10月的CPI和PPI月度時間序列數據，對模型（3）用OLS進行估計參數，得到表2和表3的結果。

表2 模型（3）第一個方程即CPIt+1參數估計結果

表3 模型（3）第二個方程即PPIt+1參數估計結果

從表2和表3中可以看出，兩個方程的F值和每個變量的T值都在5%的水平下顯著，調整后的很高，所以模型有很好的解釋能力。由于CPI和PPI是時間序列變量，很可能是非平穩變量，變量之間是否存在協整關系對C-PNLDS模型非常重要，所以還要用EG兩步法對其進行協整檢驗，檢驗結果見表4和表5。

表4 序列平穩性檢驗表

從表中的檢驗結果可以看出CPI和PPI兩個變量在沒有差分時T統計量的值均大于5%顯著水平下MacKinnon臨界值，說明這兩個是非平穩變量，而在一階差分后T統計量的值均小于5%顯著水平下MacKinnon臨界值，說明是平穩的。其殘差、T統計量的值均小于5%顯著水平下MacKinnon臨界值，說明u1、u2也是平穩的，所以模型變量之間具有協整性，即存在長期的穩定關系。

因此，可以由模型（3）可以近似的轉化為模型（2），最終得到的C-PNLDS模型為：

模型中有3個非線性項，而且第二個方程時間變量在5%的水平下是顯著的，所以該系統為非自治非線性動力系統。這兩個方程具有明顯不同的增長機制，CPI方程包含一個一階正反饋，表示方程有自我增長機制；還包含一個二階交互項，且系數是負的，表明PPI對CPI有加速抑制的作用。PPI方程包含一個一階正反饋項，表明方程具有自我增長機制；方程又包含一個負的耦合項，表明耦合項（CPI與PPI的乘積項）對PPI有不利的影響，CPI和PPI是共棲偏害的關系；CPI的系數是負的，表明CPI對PPI有抑制作用；方程中還包含一個二階交互項（CPI的平方項），且系數是負的，表明CPI對PPI有加速抑制的作用。

3 結果分析

CPI與PPI之間呈現的上述這種非線性的關系似乎有悖常理，但是結合內容構成和現實經濟的運行狀況進行分析就會看得很清楚。

CPI的調查內容分別為食品、煙酒及用品、衣著、家庭設備用品及服務、醫療保健及個人用品、交通和通信、娛樂教育文化用品及服務、居住等八大類。其權重分別為34%、4%、9%、6%、10%、10%、14%、13%，其中工業消費品的權重大約占了一半，而另一半是食品和服務項目。PPI的調查內容分為生產資料和生活資料，大部分的調查內容是原材料、電子、化工等生產資料，大約占2/3，而用于居民最終消費的生活資料只占1/3。所以，消費品價格上漲對CPI的影響大過對PPI的影響，原材料價格的上漲對PPI的影響大過對CPI的影響。

結合現實的經濟情況來看，從2007后半年開始到2008年8月由于原油、煤炭等自然資源的匱乏，導致原材料價格的大幅度上漲并直接推動PPI飛漲，最高在2008年8月達到110.1。而從2007后半年到2008年2月CPI大幅上漲，最高達到108.7，其原因是在此期間以豬肉為代表的食品類產品價格迅速大幅上漲帶動的。而在國家相關政策和市場機制自我調節的作用下，食品價格逐漸得到了有效的控制。并且2008年我國出口量大幅減少，造成了產能過剩，國內供給增加，加快了物價下降，進而使CPI下降。上述原因使得CPI從2008年2月開始呈逐漸下降態勢。所以，從2008年2月到2008年8月CPI是逐漸下降的，而PPI是上漲的，類似CPI與PPI倒掛的現象在2004年后半年也有出現，這里就不做詳細的分析。

可見，由于二者構成不同，食品價格得到控制逐漸下降，產能過剩導致物價下降，使得CPI逐漸下降；而原材料價格飛漲推動PPI快速上漲，進而導致了二者出現了倒掛的現象，這種現象進而導致了PPI對CPI有加速抑制的作用、CPI對PPI有抑制作用及二者是共棲偏害的關系，即模型（4）中第一個方程中PPI平方項的系數和第二個方程中CPI和CPI*PPI的系數是負的。

4 與VAR模型的比較

現有的對CPI和PPI關系研究的主要方法是向量自回歸模型，即VAR模型。但是VAR模型揭示的只是CPI和PPI兩者之間的線性關系。本文不對VAR模型的建模過程進行詳細闡述，只對比VAR模型和C-PNLDS模型的結果，進而可以比較出這兩種模型在揭示CPI和PPI關系上的優劣。

從表4的結果中可以看出，C-PNLDS模型得出的CPI和PPI調整后的R2都比VAR模型得出的R2要高，這說明C-PNLDS模型比VAR模型的解釋效果要好；而且C-PNLDS模型得出的CPI和PPI的AIC值都要比VAR模型得出的AIC值要小，這也說明用C-PNLDS模型來分析揭示CPI和PPI的關系比VAR模型的效果要好。

5 結論

從以上分析，我們可以得出：整個C-PNLDS模型為非自治非線性動力系統；CPI具有自我增長機制，PPI對CPI有加速抑制的影響，即PPI的平方項對CPI有負的影響；PPI也具有自我增長機制，CPI自身對PPI的增長有抑制作用，但它的平方項加速了PPI的增長，耦合項對CPI無影響，而使PPI受損，所以二者是共棲（偏害）的關系。

CPI和PPI是我國宏觀經濟的兩個重要指標，對宏觀經濟政策的制定有著重要的作用，本文運用非線性動力系統，建立了C-PNLDS模型，揭示了二者之間的非線性關系，希望能對各位學者更清楚地認識和更深入地研究二者之間的關系有所幫助。

表5 參差平穩性檢驗表

表6 C-PNLDS模型和VAR模型主要參數值對比

[1]徐國祥.統計指數理論及應用[M].北京：中國統計出版社，2004.

[2]羅納德·肖恩.動態經濟學[M].北京：中國人民大學出版社，2003.

[3]趙國慶.尋求我國GDP對FDI的最優依存度與FDI最優規模—基于1980～2003年我國GDP與FDI非線性動力系統的研究[J].管理世界，2006，（1）.

[4]劉文華.正確看待PPI和CPI的差異[J].中國統計，2005，(7).

F222.1

A

1002－6487（2011）07－0030-03

鄧月明（1985-），男，吉林長嶺人，碩士研究生，研究方向：統計學方法與應用。李興緒（1967-），男，云南昆明人，博士，教授，研究方向：統計學方法與應用。

（責任編輯/亦民）