Black-Scholes期權定價的修正模型及其應用性研究

陳溟

（內蒙古科技大學數理與生物工程學院，內蒙古包頭014010）

Black-Scholes期權定價的修正模型及其應用性研究

陳溟

（內蒙古科技大學數理與生物工程學院，內蒙古包頭014010）

文章在經典B-S模型的基礎上引入了交易費用和連續支付的紅利，對期權定價公式進行了進一步研究，并且給出了存在交易費用和連續紅利時的期權定價公式。通過馬鋼權證和云化權證的實例分析，進一步說明有交易費用和連續紅利存在對期權價格的影響，并對結果進行簡要的分析。

B-S定價模型；交易費用；連續紅利

1973年，美國芝加哥大學教授Black.F和斯坦福大學教授Scholes.M發表了一篇名為《The pricing of options and Corporate Liabilities》的著名論文，文章給出了Black-Scholes期權定價模型，推導出基于股票的任何一種衍生證券的價格應滿足的微分方程，并成功地求解該方程，因此獲得諾貝爾經濟學獎。該理論及其以后的多種變形，對金融衍生工具市場的發展起了很大的推動作用。

經典的Black-Scholes模型在研究過程中沒有考慮交易費用和連續紅利，這使得該模型在現實金融市場中的實用性降低。為了提高該模型的實際應用性，使其更加符合現實的金融市場，本文在Black-Scholes模型假設的基礎上，引入了交易費用和連續紅利，并且給出了存在交易費用和連續紅利情況下的期權定價公式，然后又引進兩個具有代表性的權證，進一步研究分析，從而說明交易費用和連續紅利的存在對期權價格的影響。

1 Black-Scholes期權定價模型及其修正模型

期權定價的Black-Scholes偏微分方程為：

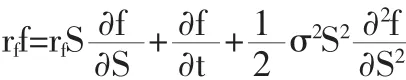
對應于可用標的變量S定義的所有衍生證券，此方程有許多解。解方程時得到的特定的衍生證券取決于使用的邊界條件。對于歐式看漲期權，關鍵的邊界條件為：

f=max(S-X,0)當t=T時

對于歐式看跌期權，關鍵的邊界條件為：

f=max(X-S,0)當t=T時

求解該偏微分方程，可得歐式看漲期權定價公式為：

C（S，t）=SN(d1)-Xe-rf(T-t)N(d2)

看跌期權定價公式為：

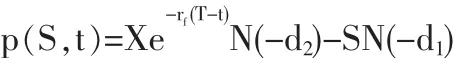
其中：

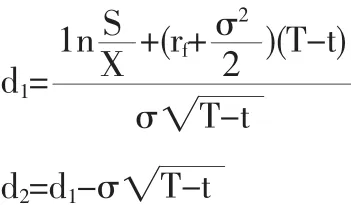
N(x)為均值為0標準差為1的標準正態分布變量的累計概率分布函數，f為期權價格，f=f(S,t)，S為股票價格，X為執行價格，T為到期日，σ為股票回報的波動率，rf為瞬時無風險利率。

實際金融市場中，股票投資者經常會得到一定數量的紅利，紅利的支付有兩種情形，每年在規定時間內支付或者按照一定比例連續支付，這里為方便只討論連續支付的情形，在規定時間內支付可將除權除息日所支付的紅利均攤到每一天，這樣便可認為紅利是連續支付的。現實交易中由于對投資組合的權重進行連續調整可引起交易成本不斷增加，所以在修改模型時將交易成本考慮在內成為必然。Black-Scholes期權定價模型是在連續條件下，先在dt時間內對期權進行套期保值，再令dt→0而得到的，當考慮交易費用時，就不能無限次地對其進行套期保值，否則交易費用也會達到無窮，這是不可能的。因此，我們可適當修改該模型基本假設里的部分條件，對Black-Scholes方程基本假設做如下推廣：

(1)股票價格過程遵循幾何布朗運動，其離散形式為：

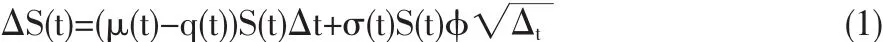
其中，準～N(0,1)其概率密度函數為：

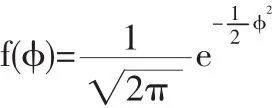
這里△t不再是無窮小量，不再求趨于0的極限。

(2)期權在時刻t的價值遵循伊藤引理，其離散形式為：

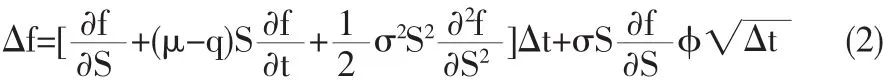
(3)股票連續支付紅利，利率為q(t)，無風險利率為r=r(t)。

(4)交易費用是投資者因買賣股票而產生的直接費用，一般由股票多頭支付,并以交易額的固定比例M來表示。

構造投資組合π，買入一份期權合約f，賣出δ份股票S：

π=f-δS

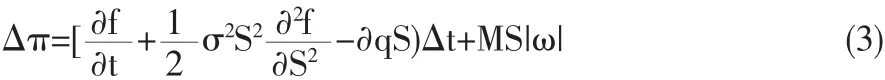
（3）式因套期保值策略而產生的交易份額ω為：

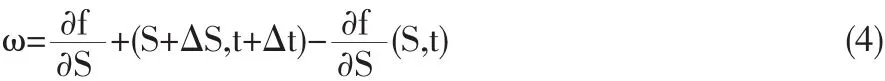
利用泰勒中值定理,將(4)式的第一項展開得：

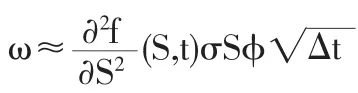
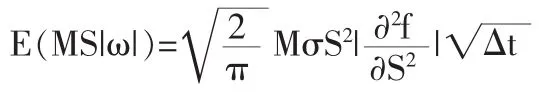
從而可得△π的數學期望為：

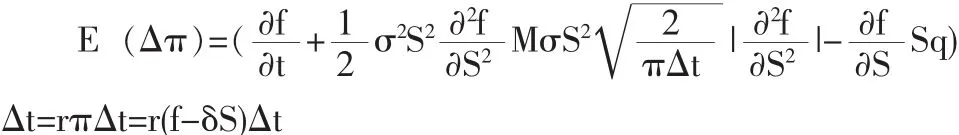
兩邊同時消去△t并移項，即可得到有交易成本和連續支付紅利情況下歐式期權多頭的定價方程為：

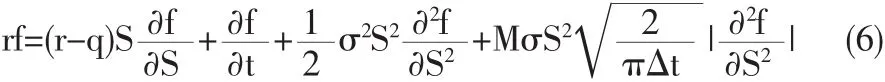
歐式期權空頭的定價方程為：

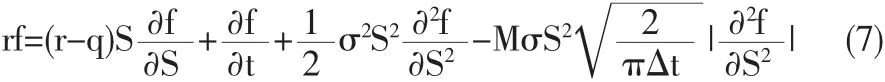
2 求解修正后的Black-Scholes期權定價方程

用偏微分的知識來求解該方程比較繁瑣，我們可以根據Black-Scholes模型的公式來推廣有交易費用和連續支付紅利的情況。將此股票與一只不支付紅利的相似股票進行比較，紅利的支付使得股票價格降低，所以支付連續紅利率q使得股票價格的增長率比不支付時減少了q。

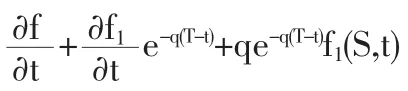
帶入(6)式中，整理后，可得：

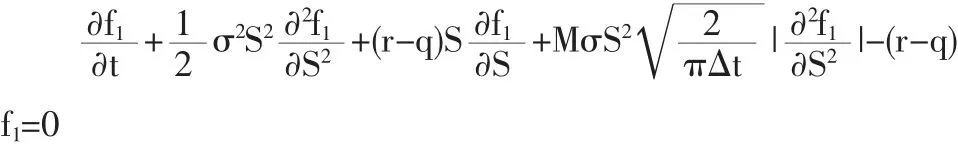
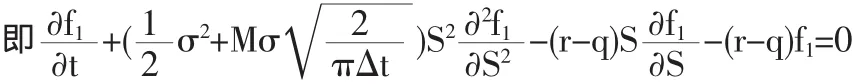
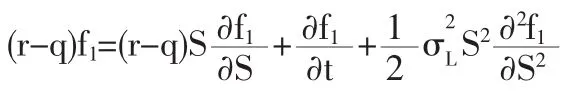
與B-S基本模型相比，我們可以看出有交易費用和紅利的定價模型只差在無風險利率r上，只需r-q用代替r，便可得到有交易費用和紅利的期權定價公式。

于是，有交易費用和紅利的歐式看漲期權定價公式為：

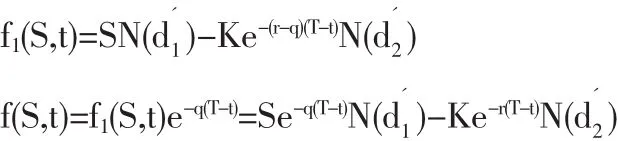
其中

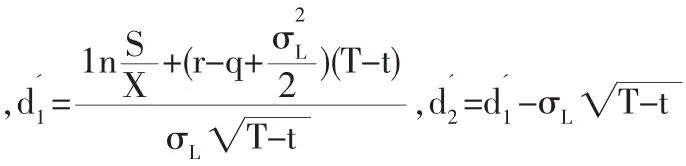
3 添加交易費和連續紅利的期權定價公式的應用研究

我們選取兩個具有代表性的權證—馬鋼權證和云化權證。馬鋼權證選擇2006-11-29至2008-11-28時間段，云化權證選擇2007-3-8至2009-3-7時間段（見表1），通過比較二者的B-S理論價格與修正價格的差異，進而說明交易費用和連續紅利對期權價格的影響。

3.1 馬鋼權證和云化權證的理論價格

3.1.1 馬鋼權證的理論價格

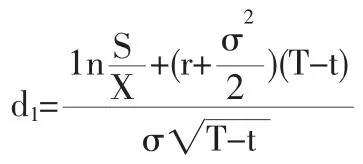
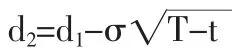
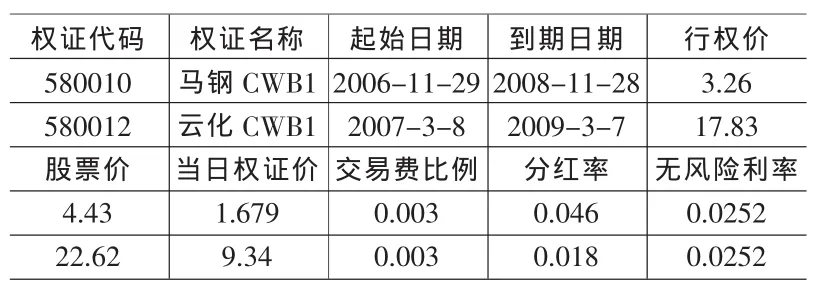
表1 馬鋼權證和云化權證的有關數據

由表1可得，S=4.43,X=3.26,T-t=2,r=0.0252,c=1.679，通過Matlab軟件編程，可得馬鋼權證的隱含波動率σ為0.5136，d1=1.7096,d2=0.9832

表2 B-S理論價格與有交易費和連續紅利的權證價格

查表有：N(d1)=0.956，N(d2)=0.836

則馬鋼權證的B-S理論價格為1.6437。

3.1.2 云化權證的理論價格

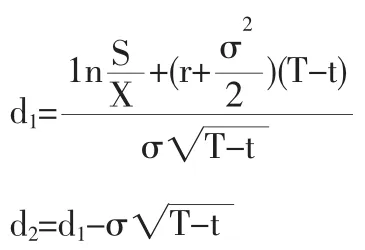
由表1可得，S=22.62，X=17.83,T-t=2,r=0.0252,c=9.34通過Matlab軟件編程，可得云化權證的隱含波動率σ為0.6543，d1=1.5486,d2=0.6232

查表有：N(d1)=0.9384，N(d2)=0.7295

則云化權證的B-S理論價格為8.8589.

3.2 考慮有交易費和支付連續紅利情況下的權證價格

3.2.1 馬鋼權證的修正價格

有交易費用和支付紅利時的期權定價公式為：

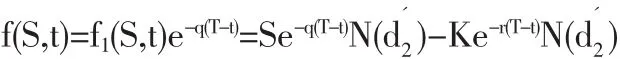
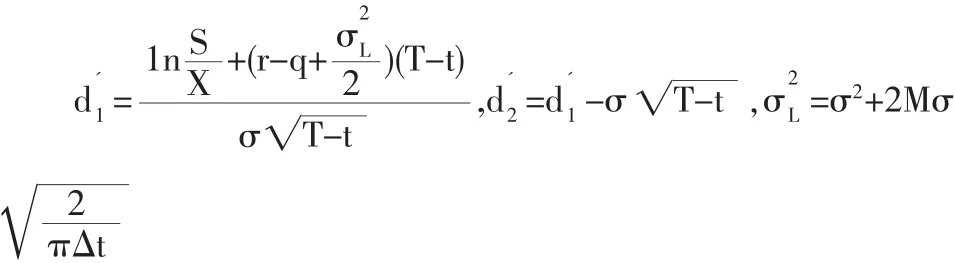
馬鋼權證相關數據：S=4.43,X=3.26,T-t=2,r=0.0252,q=0.046,M=0.003

又由上可得馬鋼權證的隱含波動率為0.5136，則可計算σL=0.517

那么可求得有交易費用和紅利的馬鋼權證的修正價格為1.3836。

3.2.2 云化權證的修正價格有交易費用和紅利時的期權定價公式為：

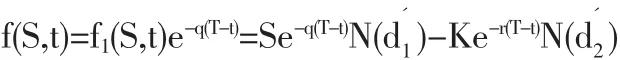
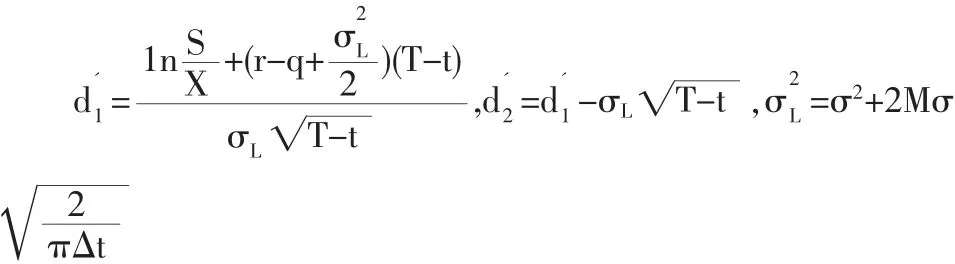
云化權證相關數據如下：

S=22.62,X=17.83,T-t=2,r=0.0252,q=0.018,M=0.003,σ=0.6543,σL=0.6577

則可得有交易費用和紅利時的云化權證的修正價格為8.3104.

3.3 結果分析

馬鋼權證和云化權證的B-S理論價格與修正價格見表2與圖1、圖2。

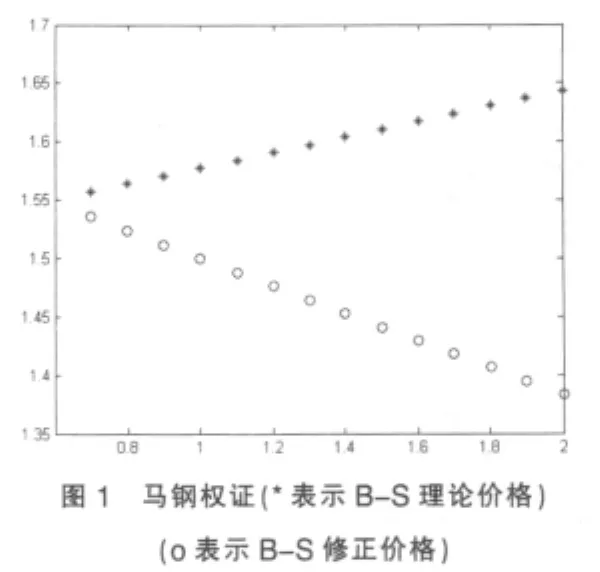
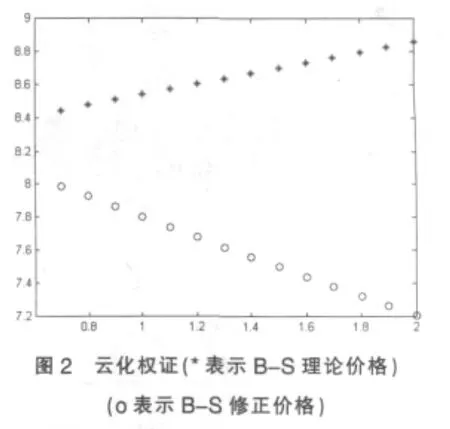
根據以上實證分析，我們將有交易費用和支付連續紅利情況下的權證價格與經典的B-S定價模型的結果進行比較分析，結果如下：

（1）從散點圖中我們可以看出，有交易費用和連續支付的紅利存在時的權證價格比B-S理論價格偏低。

（2）對于馬鋼權證來說，考慮交易費用和支付連續紅利情況下的權證價格比經典的B-S定價模型的權證價格降低了15.82%.

（3）對于云化權證來說，考慮交易費用和支付連續紅利情況下的權證價格比經典的B-S定價模型的權證價格降低了6.19%。

目前，我國權證市場中，交易費用一般為千分之三，如果大客戶和券商協議降傭，那么交易費用將更低，特別是在目前我國股市還沒有做空機制的情況下，不能無限次地進行套期保值，所以就一次單邊交易而言，交易費用通常可以忽略不計。

[1]約翰·赫爾,張陶偉譯.期權、期貨及其它衍生產品[M].北京:華夏出版社，1999.

[2]姜禮尚.期權定價的數學模型和方法[M].北京：高等教育出版社，2003.

[3]鄭曉迎，陳金賢.有交易成本的期權定價研究[J].電子科技大學學報，2000.

[4]李春泉,劉新平.Black-Scholes模型期權定價方法及其應用[J].重慶工商大學學報:自然科學版,2006,23(4).

F201

A

1002－6487（2011）07－0135-03

陳溟（1972-），男，內蒙古包頭人，碩士，副教授，研究方向：金融數學。

（責任編輯/亦民）