基于時間權重的回歸預測模型
殷春武
(西京學院,西安710123)
基于時間權重的回歸預測模型
殷春武
(西京學院,西安710123)
文章充分考慮新舊歷史數據對預測結果影響程度不同,探討并給出了確定時間權重應該滿足的條件,且基于所給時間權重建立了基于時間權重的回歸預測模型,在預測值和歷史數據相對誤差平方和最小的前提下推導了確定回歸預測模型的參數確定公式。該模型更符合實際預測的情況,更具有實用性。
回歸預測;模型;時間權重;參數
客觀世界中很多事物、現象、因素彼此關聯而構成關系、過程、系統。如果這種關系不便于用解析式表示時,則可以運用統計學的方法尋找這些量之間的統計關系,若這些統計關系符合最小二乘法則,則可以運用回歸分析模型進行預測。
經過各學者的共同研究和探討,關于回歸預測模型的研究和運用已經很熟練了,而且該預測方法已經成為通用的預測模型了,并在實際應用中得到較好的運用。但是通觀現有回歸預測研究可以發現,在現有的回歸預測模型的運用過程中并沒有考慮用來建立預測模型的歷史數據的新舊程度對建立模型的影響程度的大小。即對于某一社會經濟問題,由于受到市場環境、社會環境及國家宏觀調控政策等方面的影響,用來建模的近期歷史數據對于最終的預測結果的影響程度肯定要比遠期歷史數據的影響程度要大,所以在對后期數據的預測建模過程中,應該對于所采集的歷史數據的不同時期給與不同的權重,這樣建立的預測模型更符合實際情況,且預測模型的實用性和精度會進一步提高。
本文將充分考慮新舊歷史數據對模型精度的影響程度的不同,在預測值和歷史數據相對誤差最小的前提下,給出一種基于時間權重的回歸預測模型的建模過程,并給出基于時間權重的帶權回歸預測模型參數確定計算公式。
1 回歸預測模型參數確定模型的建立
針對某一預測問題,設采集到歷史數據為:y0=(y1,…,yn)T,現在針對該歷史數據,運用回歸預測模型,得到第t,(t=1,2,…,n)時期的回歸預測模型為
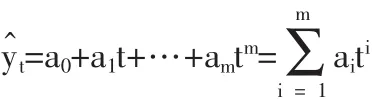
在利用歷史數據建模的過程中,一般離建模時間越近的歷史數據對后期的預測結果影響程度越大,離建模時間越遠的歷史數據對建模結果的影響程度越小,故在建模的時候應該考慮時間的時效性,為了能反映出歷史數據的新舊程度對建模結果的影響程度,可以根據歷史數據的時間先后順序對各時間段的歷史數據賦予一定的權重,即時間權重,下面給出其定義。
定義1設ht為第t時期的歷史數據對模型精度的影響程度的權重,則稱ht為時間權重。
在確定回歸預測模型的參數向量a=(a0,a1,a2,…,am)的過程中,考慮到運用回歸預測模型得到預測的值應該和實際采集到的建模數據的相對誤差的平方和盡可能的小,為此,在考慮歷史數據新舊程度不同對模型精度影響程度大小不同的情況下,建立如下帶時間權重的相對誤差最小的組合預測權重確定模型:其中時間權重為h=(h1,…,hn)
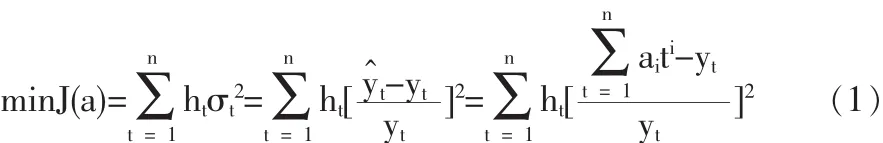
下面討論回歸預測模型的參數向量a=(a0,a1,a2,…,am)的確定。
對函數J(a)關于權重al(l=0,1,2,…,m)求導,得到
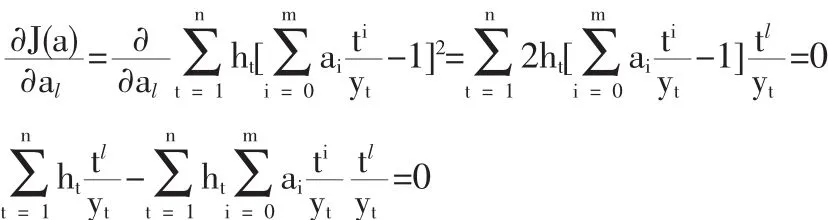
將上式寫成矩陣形式則為:
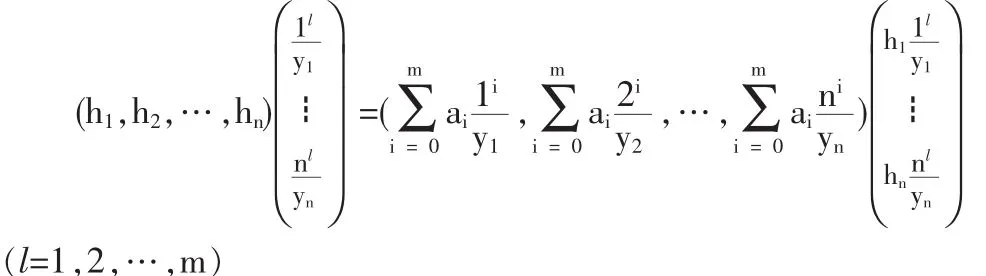

又因為(l=1,2,…,m),將所有的等式帶入則有

h·diag(y0)-1·YT=a·Y·diag(y0)-1·diag(h)·diag(y0)-1·YT
由此式從而可以得到確定回歸預測模型的參數向量a=(a0,a1,a2,…,am)計算公式為
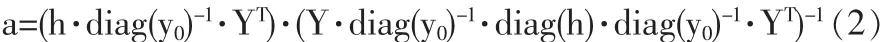
通過該計算公式就能確定出參數向量a=(a0,a1,a2,…,am)。下面給出時間權重確定的討論。
2 時間權重的討論
時間權重函數ρ(t)主要是反映第t時期的數據的對模型精度的影響程度,根據新的歷史數據對預測模型的影響程度要比舊的歷史數據的影響程度大,且相鄰兩個數據的貢獻程度差別不應該過大,同時當t無限增大的時候,最開始的歷史數據和最后面的歷史數據的貢獻程度也不能相差太遠,綜合考慮各方面的因素,時間權重函數ρ(t)應該滿足如下條件:
(1)ρ(t)在t≥1上為單調增加的正函數;
(2)ρ(t)增長趨勢應該比較平緩;

基于以上三個條件并根據已有函數的變化趨勢,通過分析,可以定義時間權重函數為…。因該函數剛好滿足了上面所討論的時間權重所滿足的三個條件。
3 結語
在以往的預測模型建模過程中,從未考慮到新的歷史數據對預測模型的影響程度比成舊數據對預測模型的影響程度要大這個因素,從而使得所建立的模型不一定符合客觀事物的發展規律。隨著統計分析以及最小二乘法的發展,回歸分析預測模型的運用已經非常普遍,本文基于客觀事物的發展規律,充分考慮了歷史數據離預測時刻的遠近程度給出基于時間權重的回歸分析預測模型,并基于歷史數據和預測數據相對誤差最小的原理,運用最小二乘法和矩陣論的原理推導了確定回歸預測模型參數的計算公式,使得回歸預測模型的理論發展有了更深層次的發展。
[1]王惠文,孟潔.多元線性回歸的預測建模方法[J].北京航空航天大學學報,2007,(4).
[2]王振友,陳莉娥.多元線性回歸統計預測模型的應用[J].統計與決策,2008,(5).
[3]王技,鐘海輝.正態模糊數時間序列的回歸預測問題研究?[J].廣州大學學報(綜合版),1998,(2).
[4]許若寧,李楚霖.一類不分明時間序列的回歸預測[J].高校應用數學學報A輯(中文版),2001,(4).
[5]董輝,傅鶴林,冷伍明.支持向量機的時間序列回歸與預測[J].系統仿真學報,2006,(7).
[6]王沫然.Matlab與科學計算(第2版)[M].北京:電子工業出版社,2005.
O21
A
1002-6487(2011)07-0161-02
殷春武(1982-),男,湖北廣水人,碩士,講師,研究方向:決策分析,預測、優化理論。
(責任編輯/易永生)

