Debye series analysis of radiation torque exerted on a sphere
LI Ren-xian,HAN Xiang-e,PARHATJAN T(,, 710071,)
1 Introduction
It is well known that transfer of angular momentum from a laser beam to a particle can produce radiation torques,which can be employed to the manipulation of microscopic objects[1],and it have been widely used in the fields of biology,physics,optofluidics,etc.The torque may be caused by circularly polarized plane wave,which carries spin angular momentum[2,3].In this case,the particle needs to be absorbing.The torque may also occur in the case of a sphere illuminated by an off-axis shaped beam[4].In this case,the off-axis beam has orbit angular momentum.It is obvious that when an absorbing particle is illuminated by an off-axis circularly polarized focused beam,both the spin angular momentum and the orbit one will be transferred from the beam to the particle.
Many researchers have been devoted to the theroretical prediction of radiation torque,and different approaches have been developed.When the size of particle is much larger than the wavelength of incident beam,i.e.d> 10λ(dis the diameter of the particle and λ is the wavelength),the geometrical optics can be employed to the prediction of radiation torque[5].Conversely,the Rayleigh model[6]can be employed to the prediction of radiation torque exerted on a particle which is much small than the wavelength,i.e.d?λ.Both geometical optics and Rayleigh model are approximate approaches.The two limiting cases can be unified by the rigorous theory“Generalized Lorenz-Mie Theory(GLMT)”[7,8],which is the solution to the Maxwell's equations and is suitable for anyd/λ.
GLMT is a rigorous electromagnetic theory,and can exactly predict the radiation torque exerted on a sphere.However,the solution is complicated combinations of Bessel fuctions,and its mathematical complexity obscures the physical interpretation of various features of radiation torque.Of all electromagnetic theories,the Debye Series Expansion(DSE),which is a rigorous theory,expresses the Mie scattering coefficients into a series of Fresnel coefficients and gives physical interpretation of different scattering mode.The DSE is an efficient tool to make explicit the physical interpretation of various features of radiation torque which are implicit in the GLMT.The DSE is firstly presented by Debye in 1908 for the interaction between electromagnetic waves and cylinders[9].Since then,the DSE for electromagnetic scattering by homogeneous[10],coated[11],multilayered spheres[12],multilayered cylinders at normal incidence[13],homogeneous[14],multilayered cylinder at oblique incidence[15],and spherical gratings[16]are studied.In our previous work,the DSE is employed to the theoretical research on the radiation pressure force exerted on a homogeneous[17]and multilayered spherical particle[18]. However, the DSE is,in our knowledge,not employed to the research on radiation torque.This paper is devoted to the theoretical prediction of adiation torque exerted on a sphere using DSE.
2 Theoretical background
We consider a sphere whose radius isaand refractive index ism1embedded in the dielectric medium of refractive indexm2.The sphere is characterized by a size parameter of 2πa/λ,where λ is the wavelength of the incident wave in the surrounding free space.The center of the sphere is located atOPwhich is the center of the Cartesian coordinate systemOPxyz.It is illuminated by a Gaussian beam whose center of beam waist is located atOG,which is the center of the Cartesian coordinate systemOGuvw,withOGuparallel toOPxand similarly for others.The coordinates ofOGin the systemOPxyzare(x0,y0,z0).The time dependent term of incident beam is exp(iωt)with ω being the angular frequency and will be omitted from all formulas.
The longitudinal radiation torqueTzand the two transverse radiation torquesTxandTyare given respectively by
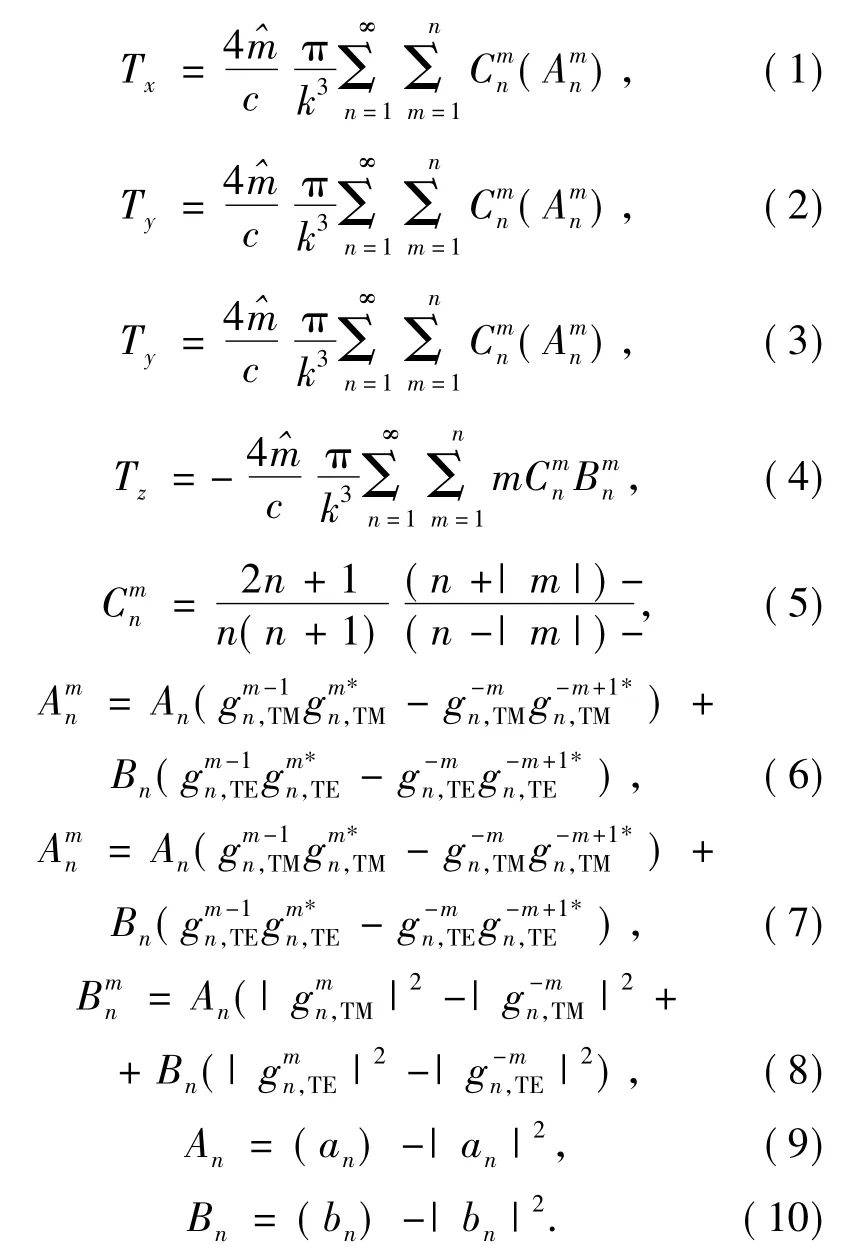
In Eqs.(1) - (3),the prefacto,in whichPis the power of the beam,is omitted.The star denotes complex conjugation.Theandare so-called Beam Shaped Coefficients(BSCs),and their expression in Bessel function can be obtained by the integrated localized approximation.For first-order Davis model,BSCs can be simply expressed by
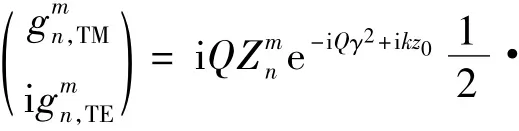
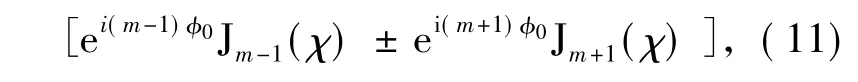
with
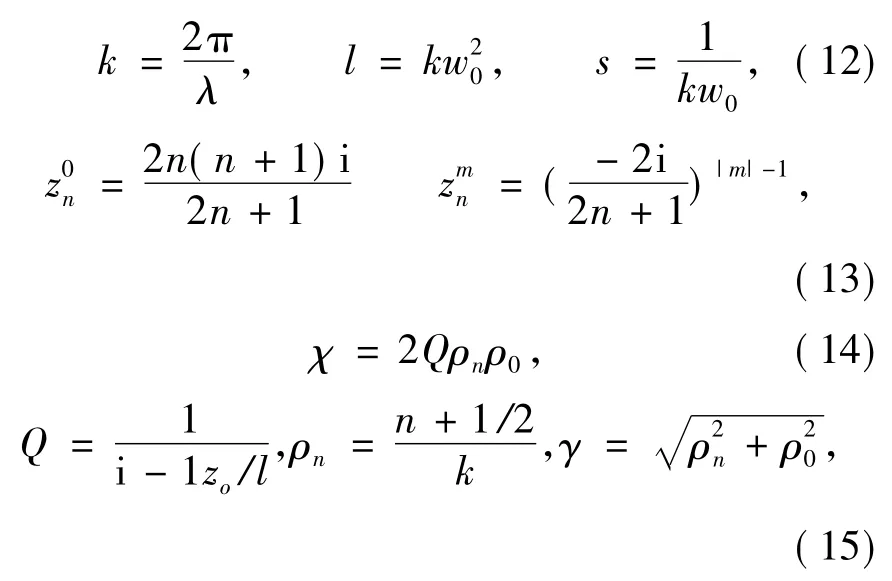
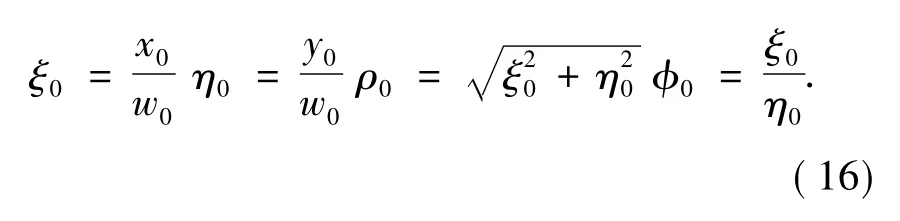
where ω0is the beam-waist radius and Jm(x)is the Bessel function of first kind.
For on-axis illumination(x0=y0=0),BCSsreduce to a single setgn,which can be calculated by using the Localized Approximation(LA)
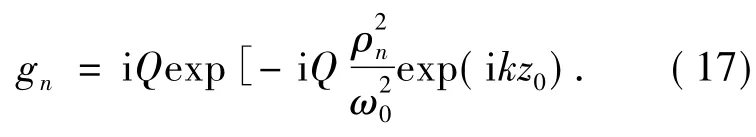
Note that we can obtain the radiation torque induced by other shaped beams by replacing the corresponding BCSs in Eqs.(11) - (17).
Theanandbnin Eqs.(1) - (10)are traditional Mie scattering coefficients,and can be expanded using Debye series as[12]
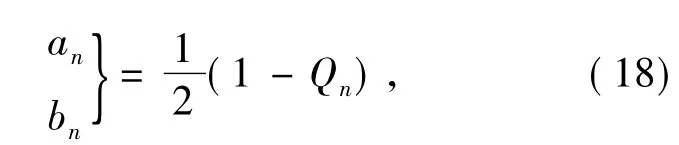
with
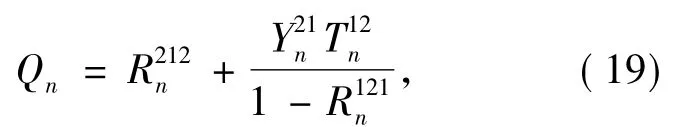
or
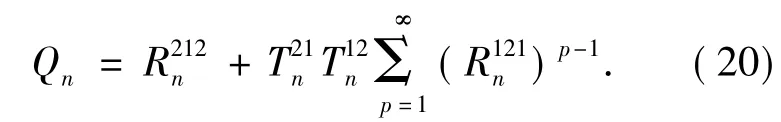
Wherepis the mode of refraction.represent respectively the portions of transmission of wave from region 2 to region 1 and from region 1 to region 2.represent respectively the portions of reflection on the surface of region 2 to region 1 and of region 1 to region 2.They are defined by
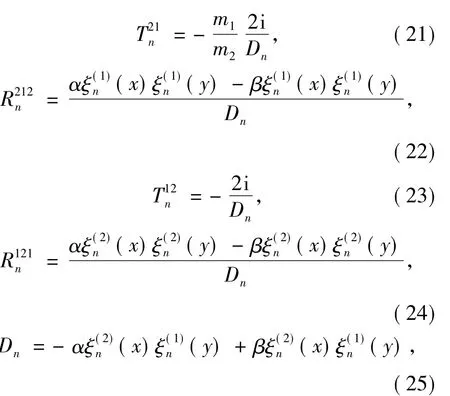
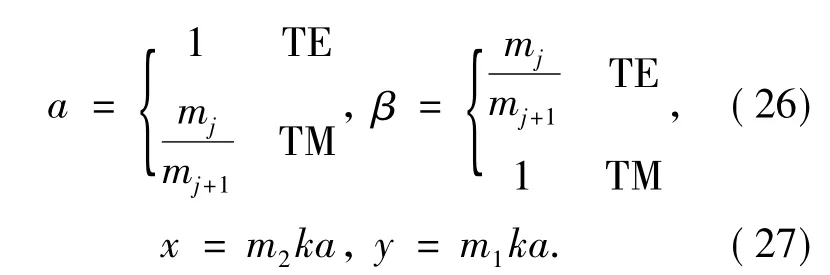
The prime indicates the derivative of the function with respect to its argument.The(z)and(z)are respectively spherical Ricatti-Hankel functions of first and second kinds Here h(n1)(z)and h(n2)(z)are respectively spherical Hankel functions of first and second kinds.
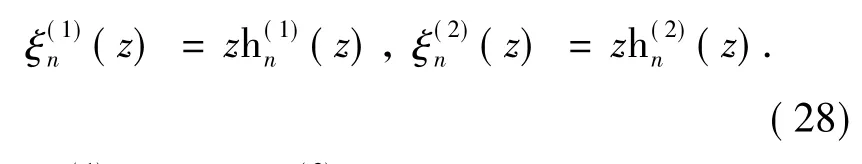
When summed overn,the first term 1/2 in Eq.(18)corresponds to the diffraction and the second term-1/2R2n12to the reflection ray.The third term is a series which describes the contribution of all modes of refraction.Each term in the series represents the contribution of that mode which undergone(p-1)internal reflections,and then emerged from the sphere.We can then choose one or several terms in the series to study their contributions and their characteristics.
3 Results and discussions
In this section,DSE is employed to the analysis of radiation torque exerted on a sphere,and the radiation torque introduced by single Debye mode or multiple modes are mainly analyzed.The cases of both linearly polarized beam incidence and circularly polarized one are considered.During simulation,we assume the particle is a hard polystyrene[19]with radius of 1.0 μm surrounded by air(m2=1.0).The wavelength of incident beam is 0.785 μm,and the beam-waist radius is 1.0 μm.
3.1 Linearly polarized beam incidence
We firstly consider the case of linearly polarized beam incidence.Here we assume the particle is a absorbing polystyrene with refractive index of 1.573-6.0 × 10-4i.When the whole summation overpin Eq.(20)from 1 to∞,the GLMT results are recovered.In fact,whenpranges from 1 to a valuepmaxlarge enough,the results obtained by DSE is identical to that by GLMT.Our results are firstly compared with that by GLMT withpmaxas parameters.In Fig.1,we depict the transverse radiation torqueTyversusx0withpmaxranges from 15 to 100.It is shown in Fig.1 that whenpmax=15,the results is very close to that by GLMT,while whenpmax=100,the results is same to that by GLMT.Herepmax=-1 andpmax=0 represent the diffraction and direct reflection,respectively.

Fig.1 Transverse radiation torque Tyvs x0for linearly polarized beam incidence(a=1.0 μm,λ =0.785 μm,w0=1.0 μm,m1=1.573 -6.0 ×10 -4i.)
We can find from Fig.1 that the torque forpmax=15 is larger than that forpmax=100 andpmax=50,while the torque forpmax=20 is smaller than that forpmax=100 andpmax=50.For explanation of such phenomena,it is necessary to isolate the contribution of single scattering process to the total torque.
Now we consider the contribution of singlepmode to radiation torque.Figs.2 and 3 give the transverse radiation torqueTyversusx0of single mode with modepas parameters.From Figs.2 and 3,we can find that all scattering processes forp=-1-5 can produce transverse radiation torque,and while the directions of torque are different.For example,the torques forp= -1 andp=3 is opposite to that for others.This can be easily expained by using geometrical optics.It can also find that the torques forp= -1,0 and 1 are much larger than that for other modes.This is caused by the decreasing of energe with the increasing of interaction between waves and particles.
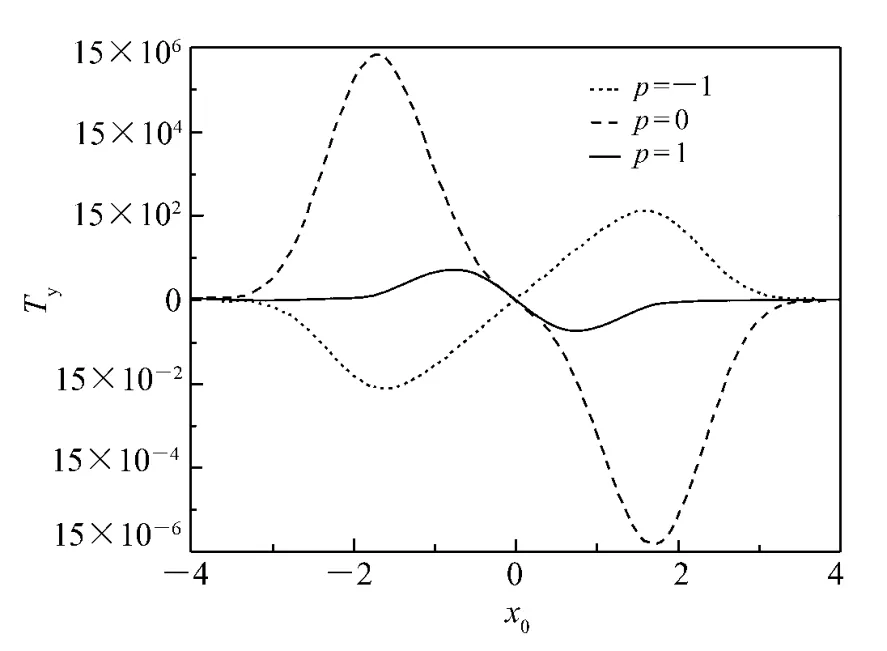
Fig.2 Transverse radiation torque Tyversus x0(p=-1,0,1)(a=1.0 μm,λ =0.785 μm,w0=1.0 μm,m1=1.573 -6.0 ×10 -4i.)
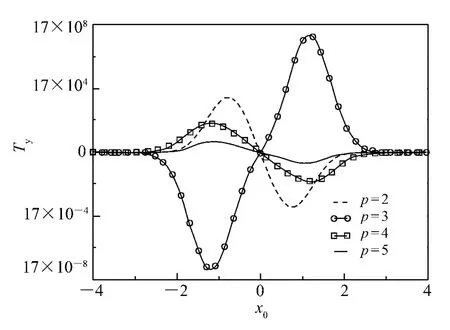
Fig.3 Transverse radiation torque Tyversus x0(p=2-5)(a=1.0 μm,λ =0.785 μm,w0=1.0 μm,m1=1.573 -6.0 ×10 -4i.)
3.2 Circularly polarized beam incidence
In this section,we focus on the case of circularly polarized beam incidence.During simulation,we assume the particle is a transparen polystyrene with refractive index of 1.573.
Similarly,we first depict the transverse radiation torqueTyversusx0with parameterspmax(see Fig.4).From Fig.4,we can firstly find that whenpmaxis larger enough,the GLMT results are recovered.It is shown in Fig.4 that the torque forpmax=50 is larger than those forpmax=15,20 or 100.
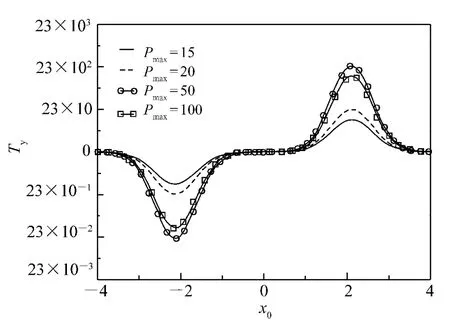
Fig.4 Transverse radiation torque Tyvs x0for circularly polarized beam incidence(a=1.0 μm,λ =0.785 μm,w0=1.0 μm,m1=1.573)
In order to obtain the physical explanation of radiation torque,we calculate the radiation torque corresponding to single scattering process,namely single Debye modep.It is depicted in Figs.5 and 6 for the radiation torque with parameters Debye modep.From Figs.5 and 6,we can find that the torques forp=-1 and 0 are much larger than those forp=1-4.This can be explained in the same way with that for linearly polarized beam incidence.We can also find that the direction of torque forp=0 is opposite with that for other modep.This can also be explained using geometrical optics.
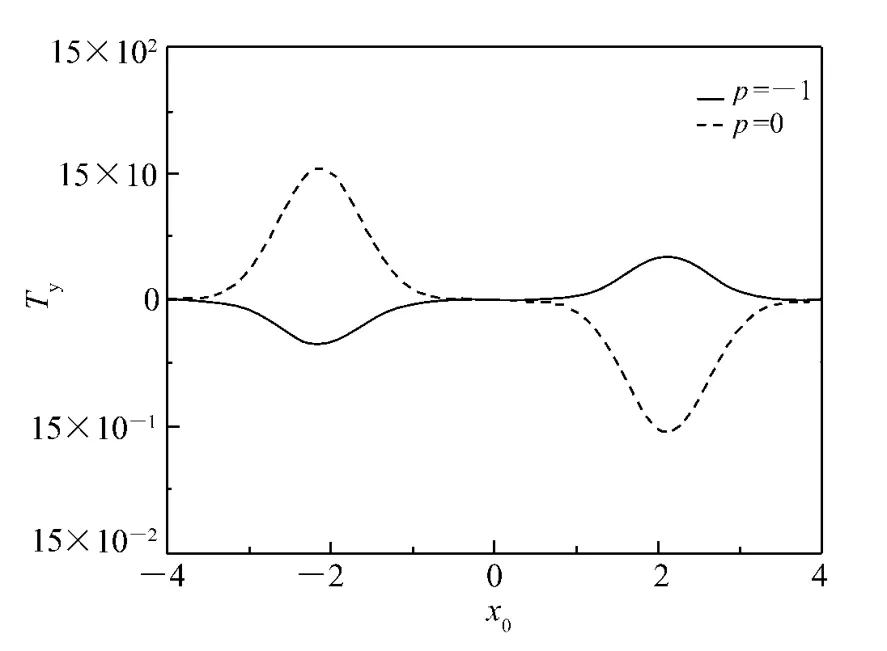
Fig.5 Transverse radiation torque Tyversus x0(p=-1,0)(a=1.0 μm,λ =0.785 μm,w0=1.0 μm,m1=1.573)
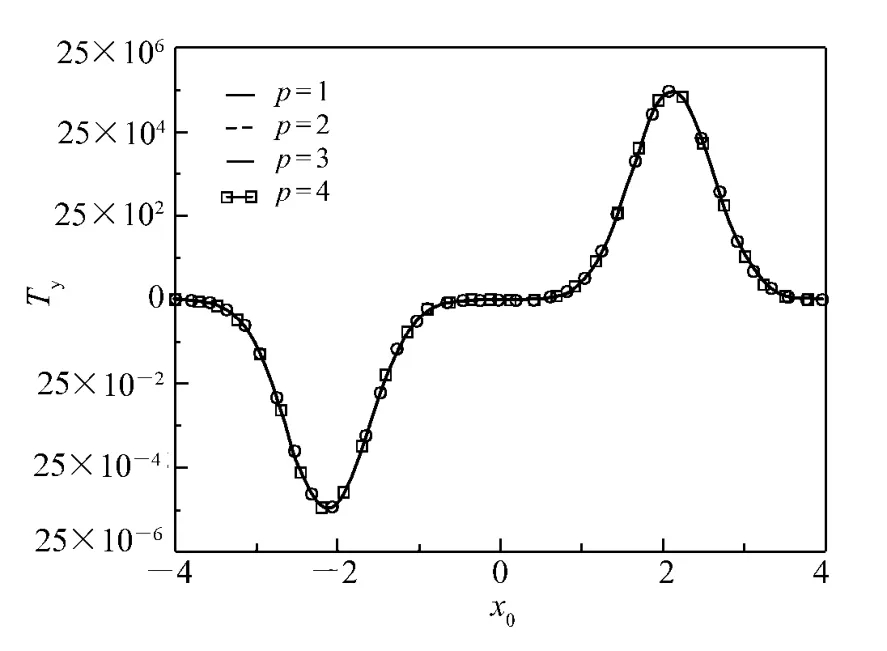
Fig.6 Transverse radiation torque Tyversus x0(p=1-4)(a=1.0 μm,λ =0.785 μm,w0=1.0 μm,m1=1.573 -6.0 ×10 -4i.)
4 Conclusions
DSE is introduced to study of radiation torque exerted on a homogeneous sphere,and it allows the analysis of contribution of single scattering process to full radiation torque,and gives the physical mechanism of radiation torque.The analysis of radiation torque corresponding to single Debye modepor multiple modes is of great importance to the improvement of optical manipulation.
Reference:
[1]ASHKIN A,DZIEDZIC J M.Optical trapping and manipulation of viruses and bacteria[J].Science,1987,235:1517-1520.
[2]FRIESE M E J,NIEMINEN T A,HECKENBERG N R,et al..Optical alignment and spinning of laser-trapped microscopic particles[J].Nature,1998,394:348-350.
[3]STEWART A M.Angular momentum of the electromagnetic field:the plane wave paradox resolved[J].Eur.J.Phys.,2005,26:635-641.
[4]CHANG S,LEE S S.Optical torque exerted on a homogeneous sphere levitated in the circularly polarized fundamentalmode laser beam[J].J.Opt.Soc.Am.B,1985,2:1853-1860.
[5]GAUTHIER R.C.Trapping model for the low index ring shaped micro-object in a focused lowest order Gaussian beam profile[J].J.Opt.Soc.Am.B,1997,14(4):782-789.
[6]ROHRBACH A,STELZER E H K.Optical trapping of dielectric particles in arbitrary fields[J].J.Opt.Soc.Am.A,2001,18:839-853.
[7]POLAERT H,GREHAN G,GOUESBET G.Forces and torques exerted on a multilayered spherical particle by a focused Gaussian beam[J].Opt.Commun.,1998,155:169-179.
[8]GOUESBET G,MAHEU B,GREHAN G.Light scattering from a sphere arbitrarily located in a Gaussian beam,using a Bromwich formulation[J].J.Opt.Soc.Am.A,1988,5:1427-1443.
[9]DEBIJE P.Das elektromagnetische feld um einen zylinder und die theorie des regenbogens[J].Phys.Z.,1908,9:775-778.
[10]HOVENAC E A,LOCK J A.Assessing the contributions of surface waves and complex rays to far-field scattering by use of the Debye series[J].J.Opt.Soc.Am.A,1992,9:781-795.
[11]LOCK J A,JAMISON J M,LIN C Y.Rainbow scattering by a coated sphere[J].Appl.Opt.,1994,33:4677-4690.
[12]LI R,HAN X,JIANG H,et al..Debye series of light scattering by a multi-layered sphere[J].Appl.Opt.,2006,45:1260-1270.
[13]LI R,HAN X,JIANG H,et al..Debye series of normally incident plane wave scattering by an infinite multi-layered cylinder[J].Appl.Opt.,2006,45:6255-6262.
[14]LOCK J A,ADLER C L.Debye-series analysis of the first-order rainbow produced in scattering of a diagonally incident plane wave by a circular cylinder[J].J.Opt.Soc.Am.A,1997,14:1316-1328.
[15]LI R,HAN X,REN K F.Generalized Debye series expansion of electromagnetic plane wave scattering by an infinite multilayered cylinder at oblique incidence[J].Phys.Rev.E,2009,79:036602.
[16]LOCK J A.Debye series analysis of scattering of a plane wave by a spherical Bragg grating[J].Appl.Opt.,2005,44:5594-5603.
[17]LI R,HAN X,REN K F.Debye series analysis of radiation pressure force exerted on a spherical particle[J].SPIE,2009,7507:750708.
[18]LI R,HAN X,REN K.F.Debye series analysis of radiation pressure force exerted on a multilayered sphere[J].Appl.Opt.,2010,49:955-963.
[19]XU F,LOCK J A,GOUESBET G,et al..Radiation torque exerted on a spheroid:analytical solution[J].Phys.Rev.A.,2008,78:013843.
- 中國光學的其它文章
- 不同氣體環境下532 nm激光誘導硅表面形貌的研究
- 皮秒激光透射率法表征高分子薄膜雙光子吸收截面
- 采用飛秒激光誘導制備彩色金屬
- 高功率準分子激光主振蕩功率放大系統光學元件的穩定性
- Formation of microstructure on liquid metal surface under nanosecond laser ablation
- Electron detachment instability and self-organization of gas discharge plasma in working mixtures of chemical non-chain HF(DF)lasers

