一類特殊矩陣特征值的絕對擾動上界＊

孔祥強

(菏澤學院數學系,山東 菏澤 274000)

一類特殊矩陣特征值的絕對擾動上界＊

孔祥強

(菏澤學院數學系,山東 菏澤 274000)

利用矩陣的奇異值分解和矩陣的計算技巧研究了 Hermite矩陣特征值的擾動界,得到了Hermite矩陣特征值的絕對擾動上界,對以往的結果進行了改進,并推廣了W ielandt-Hoffman定理。

Hermite矩陣;特征值;絕對擾動上界

設A∈Cn×n,B=A+E為其擾動矩陣,A,B的特征值分別為λ(A)={λk},λ(B)={μk}關于特征值的傳統誤差界是估計 |μi-λi|,用 Frobenius范數界定矩陣特征值與對應的按一定順序排列的其擾動矩陣特征值的所有距離的平方和的平方根,即其中m in表示對{1,2,……,n}所有的排列π取最小值,稱為矩陣的W ielandt-Hoffm an型絕對擾動上界。本文利用矩陣的奇異值分解,得到了Her m ite矩陣特征值的W ielandt-Hoffm an型絕對擾動上界,改進了以往的結果,并推廣了W ielandt-Hoffm an定理。

1.定義和引理

定義 1[1]設 A∈,存在酉陣 U、V,使得

定義 2[1](Frobenius范數)設則稱它為矩陣A的 F-范數,也可寫成

引理[2]設 A,B ∈Cn×n均為 Her m ite矩陣,X為 Her m ite矩陣且 X為正定陣,即:xHAx>0 ?x∈Cn,x≠0則:

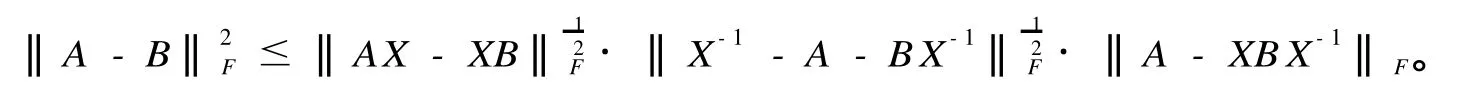
2.主要結果

定理 設 A,B ∈Cn×n,A為 Her m ite陣,即存在酉陣 P,使 A=PΛPH,Λ =diag(λ1,λ2,……λn);B為可對稱化矩陣,即存在非奇異陣 Q,使 B =QΩQ-1,Ω =diag(μ1,μ2,……μn),μi∈R;非奇異陣 X∈Cn×n,則存在 1,2,……,n的某個排列π,使得

[1]孫繼廣 .矩陣擾動分析 [M].北京:科學出版社,2001:1—226.

[2]呂烔興 .幾個矩陣范數不等式及其在譜擾動中的應用 [J].高等學校計算數學學報,2001,(2):162—170.

[3]Stewart GW.A note on non-Hermitian perturlations of Hermitian matrices,CAN-14,AD.745006,1972.

[4]Hoffman A J.andW ielandtHW.The variation of the spectrum of a normalmatrix,Duke Math.J.1953,20,37—39.

Absolute Perturbation Bounds for Eigenvalues of Herm iteMatrices

KONG Xiang-Qiang
(Department of M athematics of Heze University,Heze274000,China)

Using the singular value decomposition,some newW ielandt-Hoffman type absolute perturbation bounds of Hermite matrix are obtained.We get the results,which improve and extend the corresponding results in other papers.

Hermite matrix;eigenvalue;absolute upper bound of perturbation

O241.6

A

1671-7406(2011)03-0020-03

菏澤學院 2008年教改課題項目 (200825)。

2010-11-23

孔祥強 (1983—),男,山東菏澤人,助教,碩士,研究方向:計算數學。

(責任編輯 劉洪基)