GPS整周模糊度搜索算法的可靠性和時效性比較*

夏傳甲

(中國地震局地震研究所，武漢 430071)

GPS整周模糊度搜索算法的可靠性和時效性比較*

夏傳甲

(中國地震局地震研究所，武漢 430071)

研究了GPS載波相位快速靜態定位中的整周模糊度搜索算法，對實數編碼的改進遺傳算法和LAMBDA算法進行了對比分析。算例表明：實數編碼的遺傳算法在搜索效率和可靠性方面和LAMBDA算法相當。

整周模糊度;LAMBDA算法;遺傳算法;實數編碼;模糊度搜索

1 引言

GPS載波相位快速靜態定位的關鍵是整周模糊度的固定，這是近年來國內外GPS研究中一個非常活躍的領域［1-5］。其核心問題就是整周模糊度搜索算法的可靠性和時效性。算法的可靠性關系到整周模糊度固定的正確與否，只有固定到正確的整周模糊度，才能將載波相位觀測值轉化為高精度的距離觀測值，進而獲得高精度的點位信息;算法的時效性關系到整周模糊度固定的效率，進而影響GPS快速靜態定位的效率，因而整周模糊度固定的可靠性和時效性決定了GPS快速靜態定位的精度和應用范圍，具有重要意義［6-10］。

整周模糊度搜索算法的可靠性和時效性與搜索空間［6］及搜索方式［11］有關，搜索空間的構造一定要保證搜索結果的可靠性，而搜索方式的選擇一定要兼顧搜索的效率，因此搜索空間的構造和搜索方式的選擇是相互關聯的。本文研究了整周模糊度搜索算法的構造空間和搜索方式，分析了其特點并加以分類。并以LAMBDA算法［4，5］和實數編碼的改進遺傳算法［11］為研究對象，對其可靠性和時效性做了對比分析。

2 整周模糊度的搜索空間

整周模糊度的固定是一個從實數解到整數解的映射過程，是多對一的映射模式，由于沒有確定的數學解析式來構建實數解和整數解的關系，只能將候選值組合帶入目標函數［1］，滿足條件的組合就是所求的整周模糊度。對于目標函數而言，如果對整周模糊度的所有組合不限定條件，搜索的組合數將非常大，對搜索效率影響很大，因此需要對整周模糊度的組合加以限制，限制的過程就是構造搜索空間的過程。構造的搜索空間需要滿足兩個條件：

1)在搜索空間上的搜索等于在整個整數空間搜索，也就是說搜索空間必須包括滿足搜索準則的那一組整周模糊度，這個條件決定了整周模糊度解算結果的可靠性。

2)搜索空間必須盡量的小，這個條件決定了整周模糊度搜索的效率。

顯然，搜索算法的可靠性與時效性是相矛盾的。對于每一個整周模糊度的浮點解，構造整數空間［-d+d］，d是任意的大于零的整數，那么對于n個整周模糊度而言，就是一個以為中心的n維空間多面體，在滿足條件1)的前提下，搜索效率非常低。如果利用整周模糊度浮點解的協方差陣，則構造搜索空間［-σ0qi，+σ0qi］，這是對n維空間多面體的限制，從n維空間變成有限的空間，縮小了搜索的范圍，在保證可靠性的前提下，提高了搜索的效率，因此從統計檢驗的角度出發，劃定搜索范圍是構造搜索空間的一個辦法。在此基礎上，FARA算法［1-3］通過兩兩模糊度參數的相容性檢驗，排除不可能的候選值組合，進一步限定搜索的空間，提高了搜索的效率。這種以整周模糊度浮點解為中心，根據置信區間構造搜索范圍并利用整周模糊度參數間的相容性來加以限制的方法的思想在其他方法中得到了很多應用，比如Cholesky分解法等;遺傳算法［6-10］以整周模糊度的浮點解和協方差陣條件，利用統計檢驗的方法確定整周模糊度的范圍，完成編碼工作，然后通過選擇，雜交和變異完成遺傳過程; FASF算法［1-3］中，每一個整周模糊度的搜索范圍的確定是在其左邊模糊度序列固定的基礎上平差得到的，也就是說FASF(Fast Ambiguity Search Filter)方法每固定一個整周模糊度，就要平差一次來固定下一個整周模糊度，平差得到整周模糊度的浮點解稱為條件估值，協方差稱為條件方差，此時以條件估值為中心，以條件方差來劃定置信區間形成搜索空間。

LAMBDA算法的思路和上述方法都不同。它不是從統計檢驗的角度構造搜索空間，而是從目標函數入手。它首先對目標函數設定了合理的范圍，然后對目標函數進行矩陣分解，得到條件估值和條件方差，形成以條件估值為中心，條件方差來確定半徑的搜索橢球，那么LAMBDA算法就將n維立體空間變成了搜索橢球，縮小了搜索的范圍，提高了搜索效率。

基于上面的分析，對基于模糊度域的搜索算法進行分類(表1)。

表1 基于搜索空間的搜索算法分類Tab.1 Classification of algorithms based on search space

以二維整周模糊度浮點解和協因數陣為例，分析了改進遺傳算法和LAMBDA算法在構造空間上不同。

通過LAMBDA算法處理后得到(沒有進行降相關處理)：

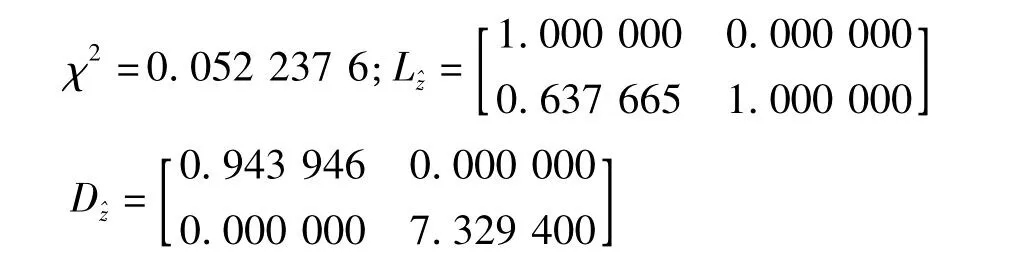
圖1 改進的遺傳算法的搜索空間Fig.1 Search space of the improved genetic algorithm

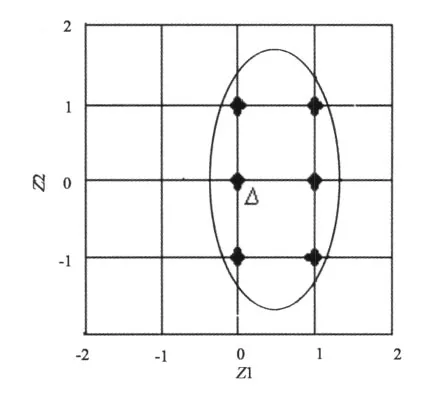
圖2 LAMBDA算法構造的搜索空間Fig.2 Search space of the LAMBDA

通過二維實例分析：以置信區間構造的搜索空間是一個矩形，而從目標函數出發構造的搜索空間是一個橢圓。在參數估計中，一個n維的整周模糊度向量服從正態分布，以FARA算法為例，每一個整周模糊度的置信度為1-α，也就是取值正確的概率為P=1-α，假設整周模糊度之間的相關性為0，整周模糊度向量取值正確的概率為P=(1-α)n＜1，因此根據置信區間構建的搜索空間取值正確的概率總小于1，但是改進遺傳算法的搜索成功率除了和初始種群有關，選擇雜交和變異也是重要的影響因子，并且遺傳過程是一個循環迭代的過程，所以取值正確的概率不是總小于1。

根據目標函數構建的搜索橢球的大小取決于χ2，只要χ2使得搜索橢球至少包含一個整周模糊度向量候選值，那么一定包含滿足目標函數最小的組合，也就是說在搜索橢球的搜索等于在整數空間內的搜索，取值正確的概率總等于1，因此χ2的選擇至關重要。

3 整周模糊度的搜索方式

在整周模糊度向量的搜索空間確定以后，只是得到了整周模糊度向量的候選值，此時整周模糊度向量的搜索變成了從整數空間到整數空間的多對一的映射關系，函數關系仍然沒有變化。

對于目標函數而言，沒有確定的數學解析式，無法完成整周模糊度向量從整數空間到整數空間的多對一的映射。在FARA算法中，在確定整周模糊度向量的搜索范圍后，整周模糊度的候選值候選值將有sum＞mn個組合，將其逐一帶入目標函數，滿足條件的組合就是所求的整周模糊度向量。在LAMBDA算法中，將目標函數進行矩陣分解得到條件估值和條件方差，然后按照序貫條件平差得到整周模糊度向量的搜索范圍，從第n個整周模糊度的固定開始一直到第一個整周模糊度，前面的整周模糊度的選擇影響了后面的整周模糊度的搜索中心和搜索范圍，通過這種序貫方式滿足條件的組合就是所求的整周模糊度向量。在FASF算法中，從第一個整周模糊度開始，每固定一個整周模糊度后，帶回整數最小二乘估計中，得到新的整周模糊度向量的條件估值和條件方差，以條件估值為中心，條件方差為置信區間構建搜索空間得到第二個整周模糊度的候選值，再固定第二個整周模糊度，以此類推通過這種回歸算法，滿足條件的組合就是所求的整周模糊度向量。

遺傳算法屬于人工智能的實現算法中的一種，它模仿生物優勝劣汰的進化機制進行逐次，并行的迭代。遺傳算法經過編碼和解碼過程，實際上是將由置信區間構建的整周模糊度向量轉化為染色體，此時對整周模糊度的搜索實際上是對染色體上基因的選擇問題，然后通過選擇、雜交和變異等過程產生新的染色體，此時滿足評價標準的染色體就是所求的新一代，然后通過不斷地循環得到最終的染色體，經過解碼后得到整周模糊度向量。

根據搜索方式對基于模糊度域的搜索算法進行了簡單的分類(表2)。

表2 基于搜索方式的搜索算法分類Tab.2 Classification of algorithms based on search pattern

4 搜索算法的可靠性分析

實驗數據來自于2010年4月9號在武漢地震計量檢定與測量工程中心采集的4個小時的采樣率是1 s的靜態觀測數據。數學模型采用短基線載波相位雙差定位模型，這種模型可以消除與距離有關的誤差項。實驗中比較了LAMBDA算法和實數編碼的改進遺傳算法的可靠性和時效性。

利用teqc對原始數據進行預處理，數據采樣率為10 s，衛星高度角是15°，每隔10分鐘截取一段數據，每段數據取6個歷元為一小段進行計算。選用L1觀測值，總計40次，前24次共有7個衛星對，后16次共有5個衛星對(表3)。

由表3可知，LAMBDA算法和改進遺傳算法大部分都能固定整周模糊度，但是也有少數例外：

1)LAMBDA算法搜索到了橢球區間內的錯誤的整周模糊度組合，這說明LAMBDA算法所采用的基于目標函數構建的搜索橢球沒有包含正確的整周模糊度組合，這也說明了雖然理論上在搜索橢球的搜索等于在整數空間內的搜索，搜索成功的概率等于1，但是由于χ2設置問題，并不能保證搜索橢球一定包含正確的整周模糊度向量候選值，這就導致了LAMBDA算法固定了錯誤的整周模糊度組合。

2)改進的遺傳算法搜索到了置信區間內的錯誤的整周模糊度組合，這表明在置信區間內的搜索不等于在整數空間內的搜索，FARA算法，FASF算法和遺傳算法的實例已經說明了這點［11］。

3)當衛星數目發生變化時直接導致模糊度浮點解發生波動從而影響兩種算法不能固定整周模糊度。這主要是估計參數的精度受到觀測條件的影響，例如衛星接收機幾何條件變化、觀測值類型、衛星數目、采樣率等。

4)兩種算法的實驗對比來看，雖然LAMBDA算法從理論上來說優于改進的遺傳算法，也就說在橢球內的搜索優于在置信區間內的搜索，但是由于改進的遺傳算法是一種全局最優化搜索算法，在編碼和搜索方式上的特點導致了和LAMBDA算法的搜索效果相當。

表3 兩種算法處理結果對比Tab.3 Comparison between the results from two algorithms

5 搜索算法的時效性分析

利用teqc對原始數據進行預處理，數據采樣率為10 s，衛星高度角為15°，參考衛星為15，其余分別為18、21、22、24、26和27。利用單歷元模型，選用L1觀測值，總計50個歷元(表4和圖3)。

表4 兩種算法搜索時間的比較Tab.4 Comparison of search time between two algorithms

圖3 LAMBDA算法和改進遺傳算法搜索時間變化圖Fig.3 Search time of LAMBDA and an Improved algorithm based on real coding

根據實驗結果的統計分析，可以得出：

從搜索時間的統計意義上來看，LAMBDA算法和改進遺傳算所需時間相當。

從搜索時間的穩定性來看，LAMBDA算法的穩定性稍好于改進的遺傳算法。

通過分析可以得到搜索算法的時效性受到下列因素的影響：

1)搜索算法的時效性與搜索空間的大小有關。對LAMBDA算法而言，經過整周模糊度降相關處理后，其相關性被降低，條件數被減小。由目標函數確定的橢球的大小取決于χ2，通過控制χ2的大小可以控制搜索橢球包含候選值的個數，所以LAMBDA算法的搜索時間大致相等，并且比較快;對于改進的遺傳算法而言，利用浮點數編碼使得所求的參數沒有增加，且占用計算機內存少，并且在雜交過程中巧妙地利用雜交前后兩個整周模糊度向量之和不變，且子代的最值為父代取或的值，最小值為父代取與的值的特點，在這個最大最小范圍內隨機產生一個子代，另一個子代則利用它們之和不變的性質來確定，從而代替二進制中的雜交，提高了雜交過程的效率，所以改進的遺傳算法的搜索時間和LAMBDA算法相當并且也比較穩定。

基于以上分析，我們可以得到：基于目標函數的Cholesky分解構造搜索空間的LAMBDA算法，可以從整體上控制模糊度候選值的個數，從而使搜索時間保持穩定的水平;基于置信區間的改進遺傳算法，雖然初始種群變化較大，但是利用浮點數編碼大大縮小參數個數，并且利用了雜交過程中特點使得搜索時間整體波動不大。

2)搜索算法的時效性與搜索方式有關。LAMBDA算法的搜索方式是序貫平差，前面的部分模糊度參數的選擇，通過參數估計直接影響了后面的模糊度參數的搜索范圍，這就是LAMBDA算法構造的以條件參數為中心，由條件方差和決定大小的搜索橢球，條件參數的確定利用了模糊度參數間相關性，充分考慮了前面模糊度參數對后面模糊度參數的綜合影響，這樣使得搜索橢球的中心更加精確，同時條件方差和原始方差相比也大大減小。改進遺傳算法的搜索方式是人工智能，通過選擇，雜交和變異等遺傳過程形成下一代的種群，這是模仿生物優勝劣汰的進化機制。這種搜索方法綜合考慮了各種因素，是一種優化搜索方式，它不僅考慮了模糊度參數間的相關性，而且考慮了各種偶然因素，因此改進的遺傳算法和LAMBDA算法的執行效果是相當的。

6 結語

在函數模型和隨機模型相同時，不同的搜索方法可能得到不同的整周模糊度整數解。通過對搜索空間和搜索方式的分析得到：基于目標函數構建搜索空間的LAMBDA算法的可靠性優于基于置信區間構建搜索空間的FARA和FASF算法［6］，基于序貫方式的LAMBDA算法的時效性優于基于逐一帶入方式的FARA算法和基于回歸方式的FASF算法［6］，而實數編碼的改進遺傳算法在可靠性和時效性方面和LAMBDA算法相當，本文研究表明以目標函數構造搜索范圍的搜索算法的可靠性和時效性不一定優于基于置信區間的搜索算法。

1 劉基余.GPS衛星導航定位原理與方法［M］.北京：科學出版社，2006.

2 李征航.GPS測量與數據處理［M］.武漢：武漢大學出版社，2005.

3 劉大杰.全球定位系統的原理與數據處理［M］.上海：同濟大學大學出版社，2003.

4 Teunissen P J G.Theleast-squares ambiguity decorrel-ation adjustment：a method for fast GPS integer ambiguity estimation［J］.Journal of Geodesy，1995，70：65-82.

5 Jonge de，The LAMBDA method for integer ambiguity estimation：implementation aspects［J］.Delf Geodetic Computing CentreLGR Series，1996，(12)：562.

6 李淑慧，等.基于搜索空間構造模糊度搜索方法的可靠性［J］.測繪學院學報，2004，21(1)：11-13.

7 劉智敏，等.遺傳算法解算GPS短基線整周模糊度的編碼方法研究［J］.武漢大學學報(信息科學版)，2006，31 (6)：607-610.

8 劉智敏，等.基于遺傳算法的高精度GPS相對定位解算研究［J］.測繪通報，2007，6：1-3.

9 劉智敏，等.基于遺傳算法的GPS單歷元單點定位方法研究［J］.武漢大學學報(信息科學版)，2007，32(1)：35 -38.

10 LiZuofa.Efficient ambiguity search using genetic algorithms［C］.ION GPS-95，California，1995.

11 夏傳甲.GPS短基線整周模糊度搜索算法的研究與實現［D］.中國地震局地震研究所，2011.

COMPARATIVE ANALYSIS OF RELIABILITY AND EFFICIENCY OF GPS AMBIGUITY ALGORITHM

Xia Chuanjia
(Institute of Seismology，CEA，Wuhan 430071)

The carrier phase ambiguity of GPS fast static positioning technique is studied，and the comparative analysis of LAMBDA and the improved real-coded genetic algorithm is made.The computation results show that the two algorithms have similar performance.

integer ambiguity;LAMBDA(Leact-squares Ambiguity Decorrection Adjustment)algorithm;genetic algorithm;real-coded;ambiguity search

1671-5942(2011)Supp.-0077-05

2011-01-26

國家自然科學基金(40974011);中國大陸構造環境監測網絡

夏傳甲，男，1984年生，碩士，主要研究方向為GPS算法的研究及其在大地測量學中的應用.E-mail：xiachuanjia@163.com

P207

A