利用神經網絡建立GPS網絡RTK的雙差對流層誤差模型*

陳遠鴻 邱 蕾 馮玉釗

(1)深圳市勘察研究院有限公司，深圳 518026 2)深圳市地籍測繪大隊，深圳518000)

利用神經網絡建立GPS網絡RTK的雙差對流層誤差模型*

陳遠鴻1)邱 蕾2)馮玉釗2)

(1)深圳市勘察研究院有限公司，深圳 518026 2)深圳市地籍測繪大隊，深圳518000)

為減小對流層誤差改正數中系統偏差的影響以提高對流層改正精度，提出了基于神經網絡的顧及空間的對流層誤差建模模型，該模型的對流層延遲誤差改正在網內外精度均達5 cm。

GPS;網絡RTK;對流層誤差;神經網絡;高程差異

1 前言

網絡RTK中GNSS數據處理的關鍵問題包括基準站間雙差模糊度的確定、流動站誤差計算與消除和流動站模糊度的確定。流動站對流層誤差的準確建模是其中一個關鍵問題。目前，常用的網絡內插模型主要是線性內插模型，該模型的本質是在平面內建立對流層誤差模型，然后進行內插得到流動站的誤差信息，同時模型的建立至少需要3個參考站。對流層延遲誤差受高程影響比較顯著，使得對流層誤差在水平方向和高程方向空間相關特性存在明顯差別，將上述模型直接應用于對流層延遲誤差改正時，由于僅僅在平面上建立對流層誤差模型，因此會引入高程方向的系統性偏差。

本文提出了基于神經網絡的空間對流層誤差建模模型，該對流層誤差模型不僅考慮了平面位置關系，同時考慮了高程因素的影響，基于空間因素對對流層進行建模，并且建模時只需要兩個參考站，因此，對于地形變化比較大的地區，應用該方法獲得流動站對流層的延遲改正信息，精度可以得到相應的提高。

2 網絡RTK對流層改正信息的提取

在網絡RTK中，由于參考站的精確參考站坐標已知，因此可以利用寬巷較長的波長特性，在短時間內固定雙差整周模糊度。然后把寬巷整周模糊度引入無電離層組合觀測方程中，用動態卡爾曼濾波，估計出L1和L2上的整周模糊度和相應的天頂距對流層延遲。L1載波的卡爾曼濾波模型在狀態向量包括L1雙差模糊度▽ΔNm，主參考站ZTDa的天頂方向延遲，副參考站ZTDb的天頂方向延遲，其狀態向量為：

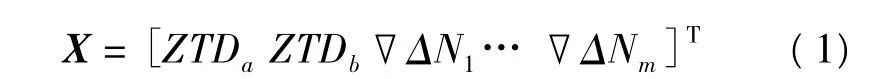
設L1雙差模糊度參數的個數為m，則狀態參數的總數為2+m。以任一衛星i的載波相位的觀測方程設計矩陣為：

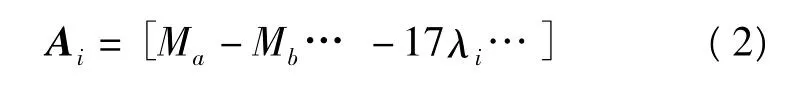
式中，Ma表示主參考站a上衛星對應的對流層延遲投影函數值，Mb表示副參考站b上衛星對應的對流層延遲投影函數值，λi表示衛星i的無電離層組合觀測值的波長。其狀態轉移矩陣為：

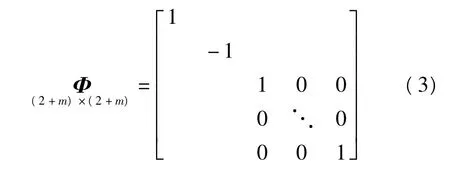
式中Φ矩陣中的空白位置均為0。對流層延遲采用隨機游走法，通過卡爾曼濾波進行估計，狀態噪聲協方差陣為：

式中，qtropa、qtropb表示對流層延遲的譜密度。ΣW矩陣中的空白位置均為0。

在估計出主參考站a和副參考站b的天頂距對流層延遲后，網絡基線上任意時刻雙差對流層延遲Δ▽可以表示為天頂距對流層延遲與其映射函數的乘積，如：

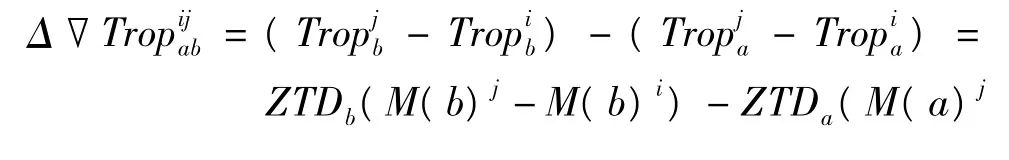
式中i為參考衛星，j為流動衛星，M(b)j為參考站b上的j號衛星的映射函數。

3 對流層高程方向的偏差

對流層延遲誤差不但受水平因子的影響，而且還受高程因子的影響。當流動站在水平方向強約束于參考站所構成的區域內時，在高程方向卻可能遠離模型區域內插面。由于高程因子影響，使由平面坐標參數估算的模型內插值與移動用戶所在高程位置上的對流層延遲真值間存在不符值，或稱為高程方向偏差［8］。

為了分析對流層在高程方向的影響，選取1個測區進行實驗(圖1)。測站的經度、緯度和高程分布如圖2所示。利用分段線性法以一個小時為間隔計算出各條基線的雙差對流層延遲，分別將6個測站2個時段的對流層延遲繪制于圖2(d)。

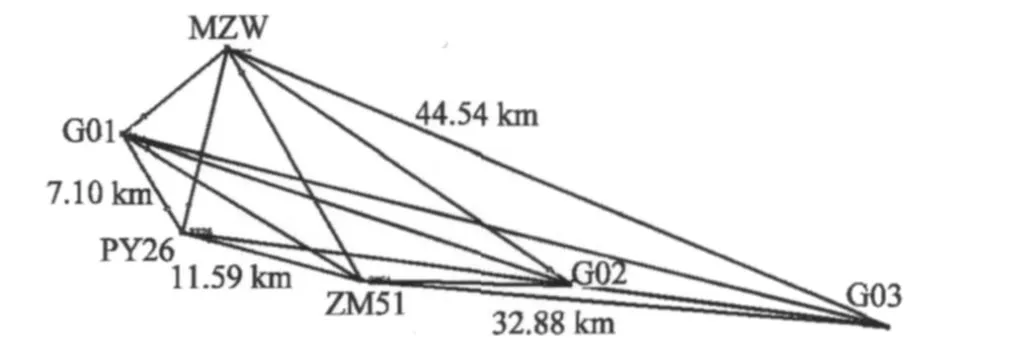
圖1 點位分布Fig.1 Distribution of stations

圖2 測站信息Fig.2 Information of stations

從圖2可以看出，單站對流層延遲都在2 m以上。6個測站的經度和緯度比較接近，但是地形起伏比較大，高程最小的點PY26與高程最大的G02，高程相差1 100 m，單站對流層延遲相差也達到了0.4 m，G02、G03、ZM51 3個點的高程比較接近，相差在100 m左右，單站對流層影響相差比較明顯，G01、ZM51、PY26 3個點的高程均在500 m以下，圖2(d)中3個點的對流層延遲相差不明顯。因此對流層延遲值與測站的高程有較強的相關性，高程越大，對流層延遲越小。對于地勢越低的地方，高程方向的影響比地勢高的地方影響大，對流層延遲值與測站的高程有一定的相關性，對于連續時間段內，對流層延遲相差比較小，差別只有厘米級。

4 基于神經網絡的區域對流層模型的建立

神經網絡模型在理論上可以無限逼近任意復雜的曲面，因此可以很好地擬合對流層延遲變化。此外，神經網絡具有較好的預測能力，可以滿足網絡RTK實時播發對流層改正數的需要。對于雙差殘余對流層延遲，只需要利用兩個參考站之間的歷元時刻、衛星的方位角雙差、X方向的方向余弦、Y方向的方向余弦、Z方向的方向余弦5個輸入量，用神經網絡技術來擬合區域對流層模型，從而實時播發對流層延遲改正數。計算步驟為：

1)選取合適的主參考站和一個副參考站，利用式(5)估計出主副參考站之間的雙差對流層殘余延遲;

2)將歷元時刻、衛星的方位角雙差、X方向的方向余弦、Y方向的方向余弦、Z方向的方向余弦作為神經網絡的輸入信號，對應的對流層延遲作為期望輸出信號，采用3層BP神經網絡模型，使用LM算法進行網絡訓練就可以得到基于神經網絡的對流層模型;

3)保存神經網絡的網絡結構和各個網絡權值，作為雙差對流層改正模型;

4)輸入流動站和主參考站的歷元時刻、衛星的方位角雙差、X方向的方向余弦、Y方向的方向余弦、Z方向的方向余弦5個量來獲取流動站的對流層延遲改正量。

5 試驗及結果分析

實驗數據與圖1的試驗數據一樣，數據采樣率為15 s，點位分布如圖1所示。計算采用網絡中部分網形，選取MZW，G01，ZM51站作為計算推值的參考點，G02站作為主參考站，G03為副參考站。以一個小時的雙差對流層殘余延遲建立BP神經網絡區域對流層模型。神經網絡結構為：5個輸入神經元，8個隱層神經元和1個輸出神經元，設置最大迭代次數為150次，迭代終止誤差為0.000 01 m。輸出神經元的激活函數為線性函數，隱層激活函數選取tanh函數：

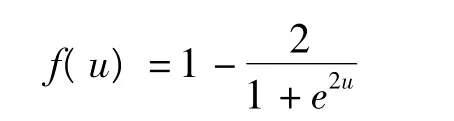
1)內符合精度檢查

利用G02、G03一小時的雙差對流層延遲進行訓練，圖3繪制了BP神經網絡模型的1小時訓練殘差，其小時的訓練殘差基本都在1 cm以內。

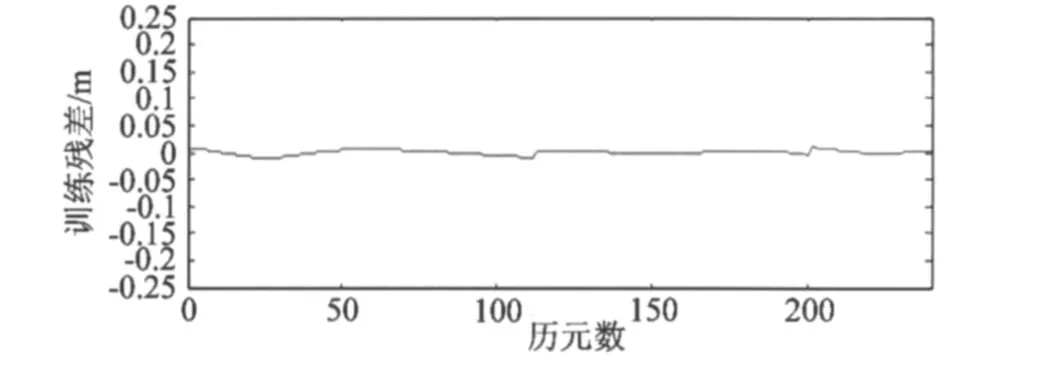
圖3 BP神經網絡模型的1個小時的訓練殘差Fig.3 Residual error plot of BP

2)外符合精度檢查

利用G02、G03一小時的雙差對流層延遲進行訓練，圖4～6繪制了基線 G02-G01、基線 G02-ZM51、基線G02-MZW的BP神經網絡模型的1個小時的擬合值(240個歷元)，并且預報了20個歷元(5分鐘)的對流層延遲量。

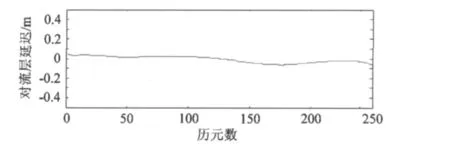
圖4 基線G02-G01雙差殘余對流層延遲Fig.4 Residual double-tropospheric delay for G02-G01

圖5 基線G02-ZM51雙差殘余對流層延遲Fig.5 Residual double-tropospheric delay for G02-ZM51

從圖4～6可以看出，BP神經網絡擬合的雙差對流層殘余延遲量都在5 cm內，在第240個歷元(1小時后)預報5分鐘的雙差殘余對流層延遲量與真值差別也在5 cm內，模型比較穩定;雙差對流層殘余延遲量呈線性變化，3條基線中G02-G01的高差最大，雙差殘余對流層延遲的變化最大，基線G02-ZM51的高差最小，雙差殘余對流層延遲的變化最小。

圖6 基線G02-ZM51雙差殘余對流層延遲Fig.6 Residual double-tropospheric delay for G02-ZM51

3)與線性內插法進行比較

為了便于比較，選取G02為主參考站，MZW、ZM51、G03為副參考站，外推G01的雙差殘余對流層延遲與真值進行比較結果見圖7。圖中最大差值為-0.073 m，與圖4中5cm的精度相比，BP神經網絡擬合的對流層模型提高了2 cm。

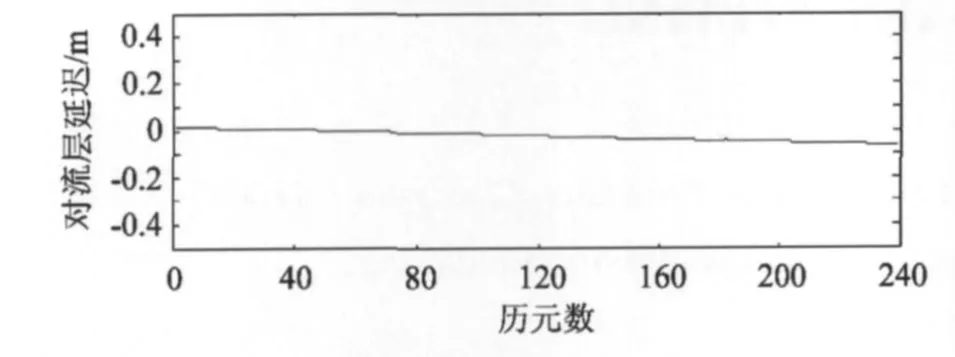
圖7 基線G02-G01雙差殘余對流層延遲Fig.7 Residual double-tropospheric delay for G02-G01

6 結束語

通過分析可以得出：網絡RTK中，對流層延遲與高程密切相關;利用BP神經網絡建立區域對流層模型僅需要兩個參考站中1小時的雙差殘余對對流層延遲進行改正，這對于連續運行的網絡CORS站是可行的。同時基于BP神經網絡的區域對流層模型考慮了對流層在空間上的分布，使得網絡RTK對流層延遲改正精度可達5 cm內，并且對于網內和網外的改正精度一樣，同時可以預報5分鐘的雙差殘余對流層改正，能夠滿足實時定位的要求。

1 Liwen Dai，et al.A study on GPS/GLONASS multiple reference station techniques for precise real-time carrier phasebased positioning［A］.ION GPS2001［C］.Salt Lake City：Palm Springs，2001：392-403.

2 王琛.基于Levenberg-Marquardt算法的用戶鑒別［J］.山西師范大學學報(自然科學版)，2005，19(2)：17-20.(Wang Chen.The authentication of the computer users based on Levenberg-Marquardt algorithm［J］.Journal of Shanxi Teachers University(Natural Science Edition，2005，19(2)：17-20)

3 熊永良，等，基于多個GPS基準站的對流層延遲改正模型研究［J］.工程勘察，2005，(5)：55-57.(Xiong Yongliang，et al.Study of tropospheric delay correction model based on multiple GPS stations［J］.Geotechnical Investigation＆Surveying，2005，(5)：55-57)

4 王勇，張立輝，楊晶.基于BP神經網絡的對流層延遲預測研究［J］.大地測量與地球動力學，2011，(3)：134-137.(Wang Yong，Zhang Lihui and Yang Jin.Study on perdiction of zenith tropospheric delay by use of BP neural network［J］.Journal of Geodesy and Geodynamics，2011，(3)：134-137)

5 徐韶光，等.長距離動態GPS數據處理在地震監測中的應用研究［J］.測繪科學，2011，36(2)：88-90.(Xu Shaoguang，et al.Applied research of long range kinematic GPS data processing in seismic monitoring［J］.Science of Surveying and Mapping，2011，36(2)：88-90)

6 陳中新，朱麗強.區域氣象特征對流層延遲模型的建設研究［J］.城市勘測，2010，(4)：93-96.(Chen Zhongxin and Zhu Liqiang.Research on the modeling of tropospheric delay based on a region atmosphere features［J］.Urban Geotechnical Investigation＆Surveying，2010，(4)：93-96)

7 高星偉，等.WAAS對流層延遲模型及其在網絡RTK中的應用［J］.測繪科學，2011，36(3)：82-84(Gao Xingwei，et al.WAAS troposheric delay model and its application in network RTK［J］.Science of Surveying and Mapping，2011，36(3)：82-84)

8 楊汀.網絡RTK定位精度影響因子與GNSS數據網絡傳輸研究［D］.中國礦業大學(北京)，2010.(Yang Ding.Research on the affected factors of positioning accuracy and network transmission of GNSS data in network RTK［D］.China University of Mining and Technology(Beijing)，2010)

A TROPOSPHERIC DELAY MODEL FOR GPS NET RTK ESTABLISHED BY USE OF ARTIFICIAL NEURAL NETWORK

Chen Yuanhong1)，Qiu Lei2)and Feng Yuzhao2)

(1)Shenzhen Investigation＆Research Institute Co.，Ltd.，Shenzhen 518026 2)Shenzhen Cadastral Surveying and Mapping Office，Shenzhen518034)

In the Virtual Reference Station(VRS)technology，atmospheric refraction error is the main factor affecting the accuracy of the long-distance RTK.However，the elevation difference between the reference plane and the roving station will cause the deviation of tropospheric error in the system and then the accuracy of troposphere correction will be lowered.A new tropospheric error model based on neural network，taking into account the space troposphere error，is presented.The accuracy of tropospheric delay model is within 5 cm，in spite of interpolation points in the network or out of network.

GPS;network RTK;tropospheric error;neural network;elevation difference

1671-5942(2011)06-0128-04

2011-07-12

陳遠鴻，男，1981年生，工程師，從事GNSS數據處理及相關測繪工作.E-mail：elalei7630@163.com

P207

A