基于相關分析的組合導航 RA IM模型研究＊

唐艷梅 王 堅 彭祥國

(1)中國礦業大學國土環境與災害監測國家測繪局重點實驗室,徐州 221116 2)中國礦業大學環境與測繪學院,徐州 221116 3)江西省水利規劃設計院,南昌 330029)

基于相關分析的組合導航 RA IM模型研究＊

唐艷梅1,2)王 堅1,2)彭祥國3)

(1)中國礦業大學國土環境與災害監測國家測繪局重點實驗室,徐州 221116 2)中國礦業大學環境與測繪學院,徐州 221116 3)江西省水利規劃設計院,南昌 330029)

探討基于相關分析理論的組合導航 R I AM方法,并給出單個和多個探測粗差的相關分析檢驗流程。通過模擬12顆 GPS和 Galileo組合導航衛星定位系統,分別給單顆和兩顆正常衛星加入粗差。仿真結果表明：觀測值的影響向量與殘差的相關系數可以定位含粗差的衛星并將粗差衛星予以剔除。

相關分析;相關系數;粗差探測;組合導航;RA I M

1 引言

隨著 GPS、Galileo等衛星導航系統的廣泛應用,用戶對導航定位的精度提出了更高的要求。特別是衛星導航系統用于民用航空領域后,給出了衛星導航系統運行的兩個重要指標：導航定位精度和完備性[1]。導航系統完備性是指當導航系統處于不健康狀態、不能準確導航時向用戶提供及時報警的能力[2,3],其核心是粗差的定位和剔除。而隨著現代測量儀器的發展,測量手段不斷趨于自動化和高效化,觀測數據大大增加,粗差也隨之增多,有學者通過分析得出：大約 1～10%觀測數據含有粗差[4]。如何定位并剔除粗差是迫切需要解決的問題,自Baarda提出粗差檢測理論后,不少學者根據其提出的思想開展了不同層次的研究,取得了大批開創性的研究成果。常用的算法有：最小二乘殘差法[5]和奇偶矢量法[6,7]。已有學者證明,兩者在粗差探測上是等效的[8]。基于相關分析理論,本文分析了測量誤差與殘差之間的關系,并利用相關分析法對相關觀測量進行粗差的檢測、定位和剔除。

2 相關系數及其檢驗

2.1 相關系數

根據相關系數的定義[9]：

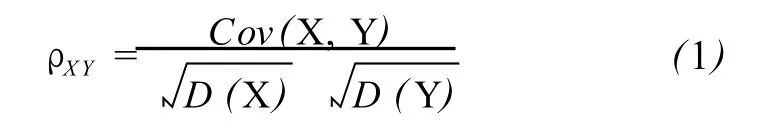
由于不能直接計算出隨機變量 X與 Y的相關系數,但可通過 X與 Y的子樣中誤差、協方差計算其估值,其計算式為：

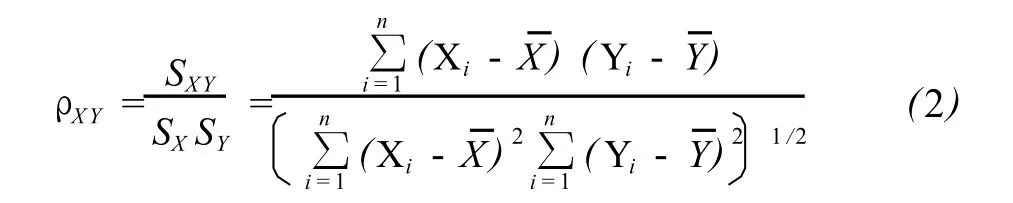
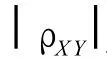
2.2 相關系數顯著性檢驗

ρ(同相關系數ρXY)的概率密度函數為[10]：

由于在實際測量中,我們只能通過相關的數理統計理論估算ρXY,為了保證所得估值的可靠性,需對估值進行檢驗。在此,可以通過直接查表或構造檢驗統計量來求得閾值ρα,本文采用直接查表的方法。在一定的顯著性水平α和自由度為γ=n-2的情況下,可通過相關系數臨界值表查得ρα的值。現做如下假設檢驗,原假設 H0：ρ=0,備擇假設 H1：ρ≠0。若由實測數據通過式 (2)計算而得的ρXY大于相關系數臨界值表中的ρα,則拒絕原假設 H0：ρ=0 (接受 H1：ρ≠0),認為顯著性水平α下 X與 Y相關;反之,則接受原假設 H0：ρ=0(拒絕 H1：ρ≠0),認為顯著性水平α下 X與 Y不相關。

3 組合導航 RA I M監測模型

3.1 相關系數的粗差探測模型

在間接平差中,測量誤差ε與殘差V的關系式為[]：

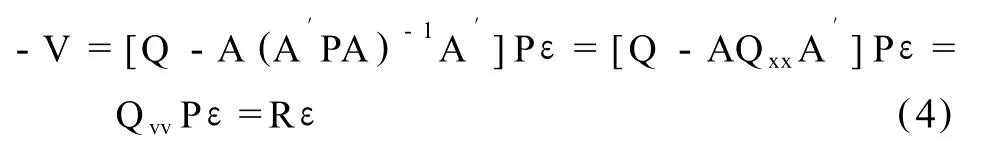
其中,A為線性化后的系數矩陣,P為觀測值的權陣,Q為觀測值的協因數陣 (Q=P-1),Qxx為參數的協因數陣,Qvv為改正數的協因數陣。對式 (4)中的R整理得：

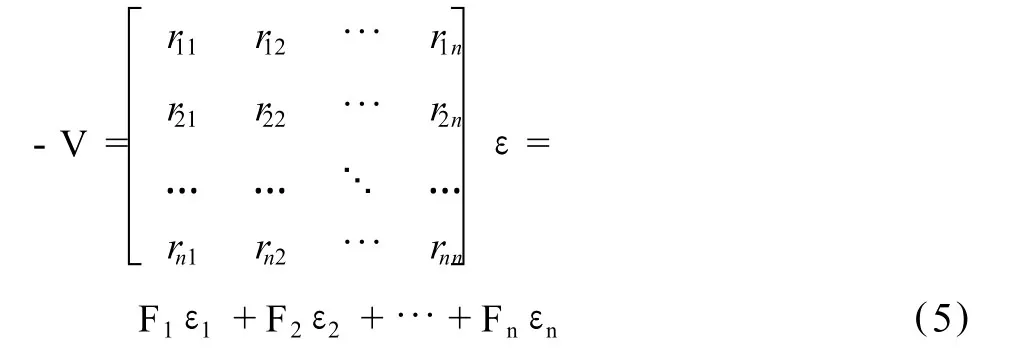
其中,Fi=[r1ir2i… rni]′,i=1,…,n,為觀測值 Li的誤差εi對殘差V的影響向量。Fi的值取決于線性化后的系數矩陣A和觀測值的權陣 P,它反映了觀測值Li的誤差εi對殘差 V的作用程度。測量誤差通過 Fi作用于 V中,Fi起到了對εi的縮放作用。當εi中不含粗差時,εi對 V的影響不顯著,V是一組偶然誤差的線性組合。若殘差V含粗差,需要檢測出含有粗差的觀測值。根據統計原理,若觀測值Li所對應的誤差εi中含有粗差,則可通過其影響向量 Fi與殘差V的相關系數來判斷。根據式 (2)可計算出 Fi與V的相關系數,即：

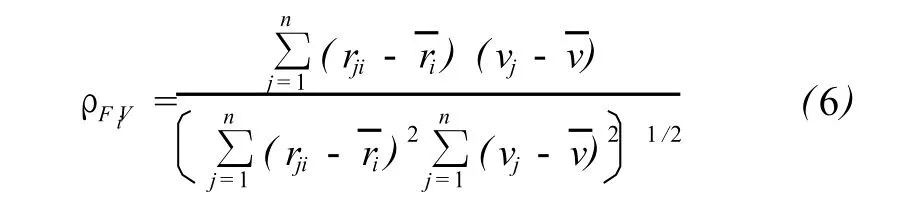
3.2 RA I M監測技術路線

RA I M性監測可由以下 4步完成：第一步：對原有觀測值進行最小二乘平差,計算殘差向量V、驗后方差。對驗后方差進行檢驗 (此處采用χα檢驗),若不通過則說明觀測值中含有粗差;第二步：計算矩陣 R和影響向量 Fi。根據式 (6)求 Fi與 V的相關系數ρFiV,并對ρFiV進行顯著性檢驗。對于給定的α,若ρFiV＞ρα,則將第 i個觀測值標記并剔除;第三步：對剩余觀測值進行第一、二步,直到檢驗通過。第四步：將第二、三步中剔除觀測值逐一恢復到平差系統中,重新平差并檢驗驗后方差。若不通過,則確認為粗差;若能通過,則認為第二 (或第三)步為誤判,并將此觀測值恢復。將最終判定為粗差的觀測值剔除后再平差,輸出結果。具體流程如圖1所示。

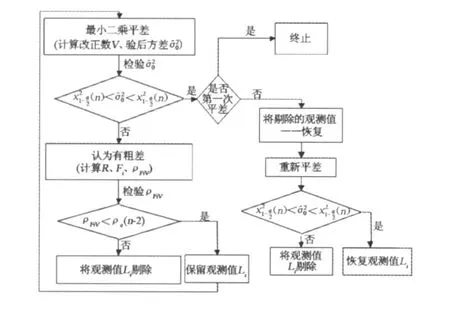
圖1 粗差探測流程圖Fig.1 Flowchart of gross error detection

4 實驗分析

以徐州地區(34.21°N,117.13°E)為例,通過軟件生成 GPS和 Gallieo衛星星座,模擬 GPS/Galileo組合導航系統,共 12顆可見衛星,其中 GPS衛星和Gallieo衛星各 6顆,衛星分布如圖 2。衛星更新頻率為 1 Hz,高度截止角為 15°。試驗中模擬了對流層誤差、電離層誤差、多路徑誤差以及噪聲誤差,衛星全天 24小時的DOP值變化如圖 3。由于 GPS與Gallieo系統誤差源基本一致,定位誤差相差不大,等值定權基本上不會影響定位結果,因此單位權方差取 2。選其中一個歷元進行分析,分別給不同衛星所對應的偽距加粗差,所得到的相關系數如圖 4～7所示。

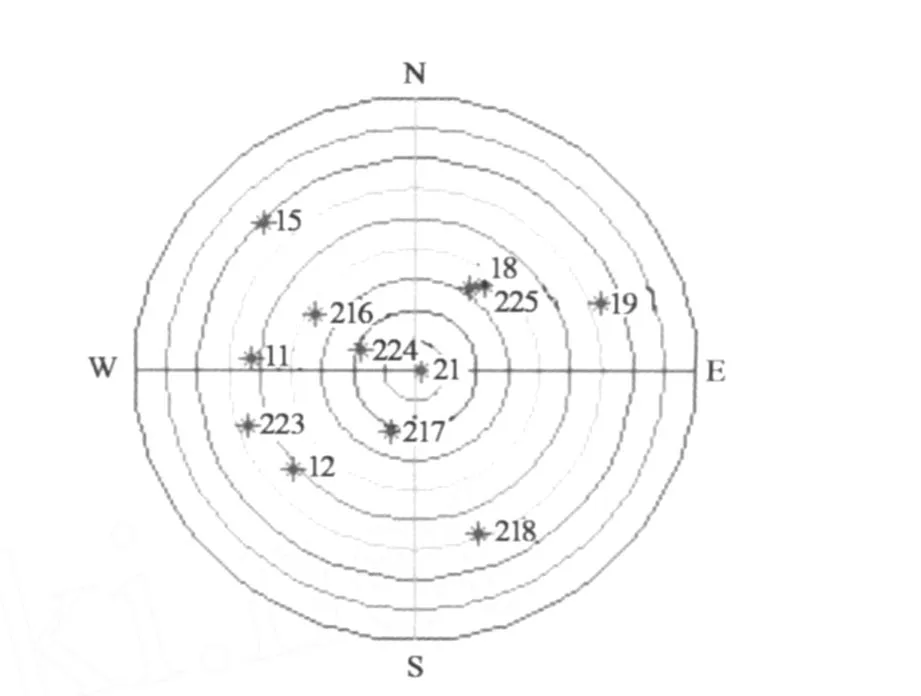
圖2 衛星分布Fig.2 Satellite distribution

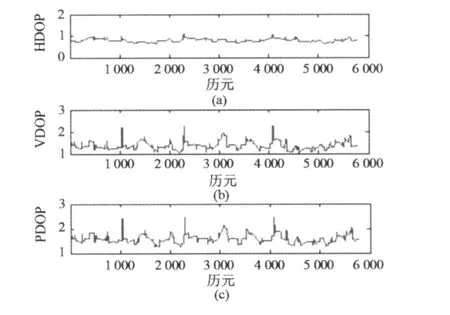
圖3 衛星24小時的DOP值變化Fig.3 Satellite’sDOP in 24 hours

圖4 PRN11加5 m粗差Fig.4 5 m gross errors plused to PRN11

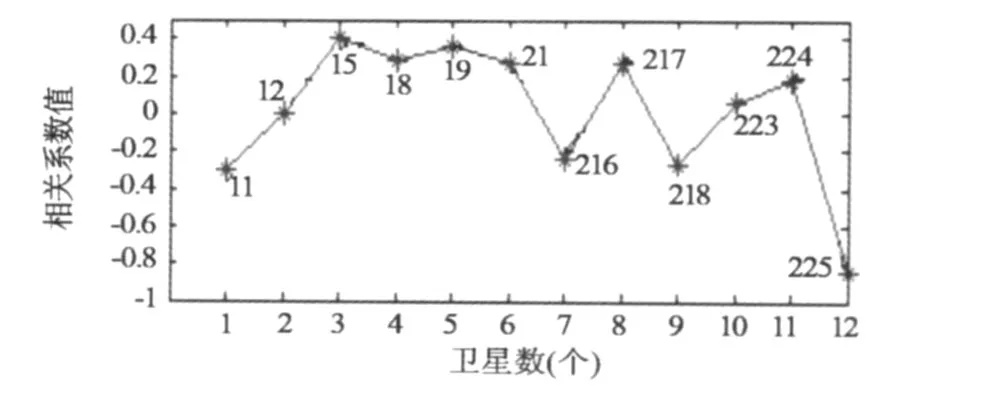
圖5 PRN225加5 m粗差Fig.5 5 m gross errors plused to PRN225

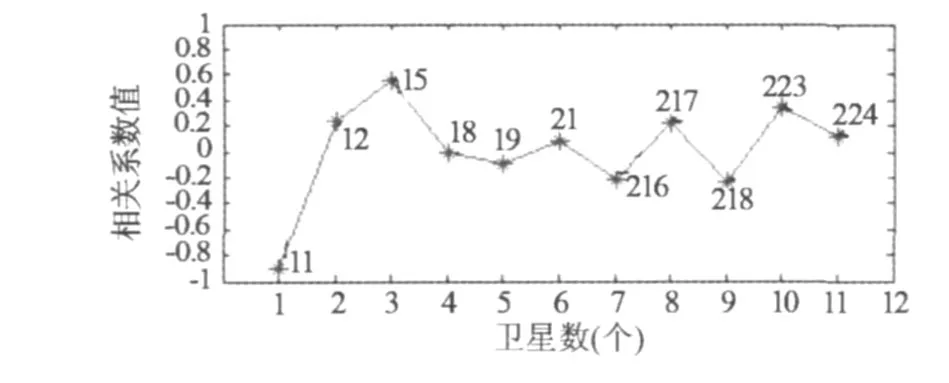
圖6 恢復PRN11Fig.6 Recovery of PRN11

圖7 恢復PRN225Fig.7 Recovery of PRN225

表1 PRN11加5m粗差Tab.1 5 m plused to PRN11 gross errors

表2 PRN225加5m粗差Tab.2 5 m plused to PRN225 gross errors

表3 恢復PRN11Tab.3 Recovery of PRN11

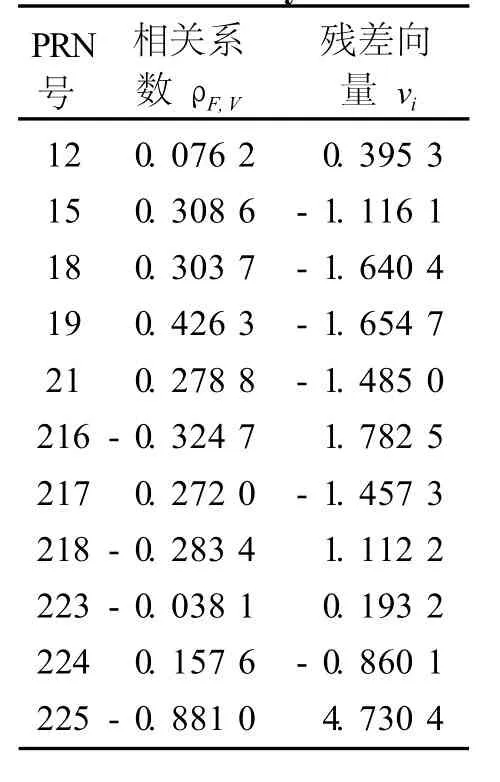
表4 恢復PRN225Tab.4 Recovery of PRN225

單粗差情況。分別給 11、225號衛星所對應的偽距加5 m粗差,各相關系數如圖4、5。顯著水平α取 0.01(下同),觀測值個數 n=12,由相關系數臨界表查得ρα(10)=0.708。由于相關系數的范圍在[-1,1]之間,圖 4、5不是很直觀,但可以看與圖 4、5相對應的表 1、2。從表 1中很容易看出只有 11號衛星的相關系數的絕對值 (0.9048)大于ρα(10),其余都小于ρα(10),且 11號衛星的殘差向量最大,說明只有 11號衛星有粗差。同樣的,從表 2中很容易發現只有 225號衛星有粗差。

多粗差情況。同時給 11、225號衛星對應的偽距加 5 m粗差,按照前文所述的方法,首先只定位到11號衛星含有粗差,先將其剔除;然后再將剩余觀測值進行平差,計算相關系數,最后定位到 225號衛星含有粗差,將其剔除。通過兩次平差計算相關系數,成功將含有粗差的觀測值找出。為避免誤判,再將 11、225號衛星分別恢復檢驗,恢復結果如圖 6、7 (對應表 3、4)。從表 3、4可以發現,恢復后兩顆衛星的相關系數值仍大于給定的閾值,說明沒有誤判,最后確定 11、225兩顆衛星含有粗差,將其剔除。進行最后的平差,輸出結果。

通過模擬實驗,對于單、多粗差,相關系數法都可成功定位粗差。顯然,單粗差比多粗差容易定位。對于單粗差,只需一步就能定位。但對于多粗差,會出現兩種情況：一種是一步就能定位出所有含粗差的觀測量;另一種是需要多次循環才能將所有含粗差的觀測量找出。第一種現象多出現于觀測量之間相關性較弱的情況。第二種多出現與觀測量間相關性較強的情況。雖然第二種情況下的多粗差定位稍有繁瑣,但相對于傳統的向前-向后選擇法簡單得多。

5 結語

GPS/Galileo組合導航中數據觀測量大,存在粗差的可能性也大,粗差的存在會大大降低導航定位的精度,甚至會產生誤導。針對這一問題,文中基于相關分析理論,利用相關分析法對模擬觀測值進行了粗差的檢測和定位。此方法對于單粗差,只需一次就可定位出含粗差的觀測量;對于多粗差,可能需要重復多次才能成功地將所有含粗差的觀測量找出。但總的來說,對于單個或多個粗差的識別效果都比較明顯。

1 秘金鐘,趙春梅,李瑋.Galileo中國區域完備性監測指標SI AMA研究[J].武漢大學學報 (信息科學版),2009,34 (10)：1 172-1 175.(Bei Jinzhong,Zhao Chunmei and Li Wei.Study on SIS MA index of China region integrity monitoring of Galileo project[J].Geomatics and Information Science ofWuhan University,2009,34(10)：1 172-1 175)

2 郭睿,鄭勇,杜蘭.GPS和 Galileo系統下 RA I M算法可用性分析[J].測繪科學技術學報,2006,23(6)：448-450. (Guo Rui,Zheng Yong and Du Lan.Analysis on RA I M availability of different navigation systems[J].Journal of Zhengzhou Institute of Surveying and Mapping,2006,23 (6)：448-450)

3 盧虎,廉杰.北斗用戶機自主完好性監測研究[J].空軍工程大學學報(自然科學版),2010,11(3)：53-57.(Lu Hu and Lian Jie.Research on RA I M algorithm ofBeidou receiver[J].JournalofAir Force EngineeringUniversity(Nnatural Science Edition),2010,11(3)：53-57)

4 Huber P J.Robust statistics[M].New York：W iley,1981.

5 黃曉瑞,田巍,李波.GPS接收機的自主完善性監測算法研究[J].遙測遙控,2003,24(1)：1-3.(Huang Xiaorui, TianWei and LiBo.Research on autonomous integritymonitoring algorithm of GPS receiver[J].Journal of Telemetry, Tracking and Command,2003,24(1)：1-3)

6 秘金鐘,李毓麟.RA I M算法[J].測繪通報,2001,(3)：7 -9.(Bei Jinzhong and Li Yulin.Research on RA I M algorithm[J].Bulletin of Surveying and Mapping,2001,(3)：7 -9)

7 秘金鐘,谷守周,方書山.基于向量相關距離的新型RA I M算法[J].中國科學：物理學 力學 天文學,2010, 40：638-643.(Bei Jinzhong,Gu Shouzhou and Fang Shushan.A new RA I M method based on vector correlation distance[J].Scientia Sinica Phys,Mechamp;Astron.,2010,40：638-643)

8 Grover R B.A baseline GPS RA I M scheme and a note on the equivalence of three RA I M methods[J].Navigation, 1992,39(3)：301-316.

9 盛驟,謝式千,潘承毅.概率論與數理統計[M].北京：高等教育出版社,2001.(Sheng Zhou,Xie Shiqian and Pan Chengyi.Probability and statistics[M].Beijing：Higher Education Press,2001)

10 李慶海,陶本藻.概率統計原理和在測量中的應用[M].北京：測繪出版社,1982.(Li Qinghai and Tao Benzao. Probability and statistics theory and application in measurement[M].Beijing：Surveying andMapping Press,1982)

11 陶本藻.測量數據處理的統計理論和方法[M].北京：測繪出版社,2007.(Tao Benzao.Statistic theory and method of surveying data processing[M].Beijing：Surveying and Mapping Press,2007)

RESEARCH ON INTEGRATED NAVIGATI ON RA I M MODEL BASED ON CORRELATI ON ANALYSIS

Tang Yanmei1,2),Wang Jian1,2)and Peng Xiangguo3)

(1)Key Laboratory forLand Environm ent and D isasterM onitoring of SBSM,CUM T,Xuzhou 221116 2)School of Environm ent and Spatial Infor m atics,CUM T,Xuzhou 221116 3)Jiangxi ProvincialW ater Conservancy Planning and Designing Institute,N anchang 330029)

The principle,calculation method of correlation coefficient,and its significance testwere described. Focusing on integrated navigation RA I M model,the integrated navigation RA I M method based on correlation analysis theorywas probed,testing processof single and multiple gross errors detectionwaspresented.By simulating the 12 GPS and Galileo navigation satellite positioning system,outlierswere added to single and t wo satellites,respectively.Simulation results show that the correlation coefficient of observations’influence vector and residual error can locate and remove satelliteswhich contain gross errors,improving the navigation positioning accuracy.

correlation analysis;correlation coefficient;gross error detection;integrated navigation;RA I M

1671-5942(2011)04-0139-05

2011-04-14

國家自然科學青年基金 (40904004);國家自然科學基金(41074010);江蘇省自然科學基金(BK2009099);教育部留學回國人員科研啟動基金;教育部博士點基金 (新教師)(200802901516);國土環境與災害監測國家測繪局重點實驗室開放基金(LEDM2009A01,LEDM2010B12);江蘇省“青藍工程”基金

唐艷梅,女,1986年生,碩士研究生,主要從事衛星導航的研究.E-mail：tymdyx@163.com

P207

A